Методы оценивания характеристик сложных помех

Отдельное внимание следует уделить оцениванию характеристик сложных помех. Термин «сложные помехи» подразумевает одновременное присутствие на изображении помех нескольких типов. Наиболее типичными комбинациями компонент сложной помехи являются следующие:

1) смесь аддитивного и сигнально-зависимого шума - модель (1.3);

2) смесь аддитивного и/или сигнально-зависимого и импульсного шума - модели (1.2) и (1.9).

Рассмотрение методов оценивания характеристик сложных помех начнем со случая, когда изображение искажено смесью аддитивных и сигнально-зависимых помех, а импульсный шум отсутствует или предварительно устранен.

Общий подход к решению задачи оценивания дисперсии таких помех предполагает построение скаттерограммы пар оценок локальной дисперсии и локального среднего, полученных на однородных участках изображения, и вписывание по скаттерограмме локальных оценок регрессионного полинома соответствующего порядка, параметры которого принимаются в качестве оценок характеристик помех [52]. Для рассматриваемых моделей смеси аддитивных и сигнально-зависимых помех (1.4), (1.6) производится вписывание полинома первого порядка [53]. Тогда коэффициент нулевого порядка будет соответствовать оценке дисперсии аддитивного шума, а коэффициент первого порядка – оценке параметра сигнально-зависимого шума.

В случае, если изображение искажено смесью аддитивных и квази-пуассоновских помех (модель (1.6)), вписывание полинома следует проводить по скаттерограмме локальных оценок дисперсии и среднего:

, (1.21)

где – оценка дисперсии в m-том блоке;

– оценка среднего в m-том блоке;

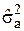– оценка дисперсии аддитивной компоненты шума;

– оценка коэффициента усиления квази-пуассоновской компоненты шума.

Если на изображении присутствует смесь аддитивного и мультипликативного шума (модель 1.4), вписывание полинома проводится по скаттерограмме локальных оценок дисперсии и квадрата среднего:

, (1.22)

где – оценка относительной дисперсии мультипликативной компоненты шума.

На точность оценивания дисперсии сложных помех оказывают влияние множество факторов, основными среди которых являются:

1) сложность обрабатываемого изображения;

2) качество детектирования однородных участков изображения;

3) точность получаемых локальных оценок дисперсии и среднего;

4) точность вписывания регрессионного полинома.

Факторы, перечисленные в пунктах 1 – 3, являются типичными для всех методов оценивания дисперсии, работающих в пространственной области, и частично были рассмотрены в подразделе 1.4, в то время как пункт 4 является специфической особенностью методов оценивания дисперсии сложных помех, поэтому рассмотрим этот вопрос более подробно.

Вписывание регрессионного полинома может производиться различными способами. Во-первых, возможно вписывание как по всем точкам скаттерограммы, так и по некоторым опорным точкам (ОТ). Как правило, локальные оценки дисперсии, полученные в блоках с близкими значениями локального среднего, при построении скаттерограммы группируются в кластеры, которые по внешнему виду напоминают облака. В качестве ОТ зачастую используются координаты центров таких «облаков», определенные тем или иным способом.

Во-вторых, вписывание может быть как неробастным, так и робастным. В свою очередь, робастность вписывания также может быть обеспечена различными способами. Если вписывание регрессионного полинома производится по всем точкам скаттерограммы, то робастность вписывания обеспечивается за счет использования специальных методов. В случае, когда вписывание регрессионного полинома осуществляется по ОТ, появляется несколько вариантов обеспечения робастности:

1) получение ОТ при помощи неробастных методов с последующим вписыванием регрессионного полинома с использованием робастных методов;

2) получение ОТ при помощи робастных методов с последующим вписыванием регрессионного полинома с использованием неробастных методов;

3) получение ОТ при помощи робастных методов с последующим вписыванием регрессионного полинома с использованием робастных методов.

Рисунок 1.9 – Пример скаттерограммы локальных оценок дисперсии и среднего с прямыми аппроксимации: истинной и полученными в соответствии с различными подходами

На рисунке 1.9 приведен пример скаттерограммы локальных оценок дисперсии и среднего с регрессионными прямыми, вписанными в соответствии с различными подходами, для изображения, искаженного смесью аддитивных и квази-пуассоновских помех с параметрами и . В данном примере для детектирования однородных участков был использован метод [41]. Аббревиатуры НВ и РВ отвечают ситуациям, когда вписывание производится по всем точкам скаттерограммы с использованием неробастной и робастной процедур соответственно. Аббревиатурами РОТНВ и РОТРВ обозначены ситуации, когда вписывание производится по ОТ, полученным робастным способом, также соответственно с использованием неробастной и робастной процедур. Справа от обозначений на рисунке приведены значения оценок коэффициента усиления квази-пуассоновского шума и дисперсии аддитивного шума, полученные по параметрам вписанных прямых. На основании приведенных данных, можно сделать следующие заключения.

1) Предварительное детектирование однородных участков с использованием даже наилучших из разработанных на данный момент методов не обеспечивает полного отсутствия аномальных локальных оценок дисперсии, в связи с чем для обеспечения более высокой точности оценивания следует каким-либо образом обеспечить робастность вписывания регрессионной прямой.

2) В пределах кластера шум условно можно считать чисто аддитивным, поэтому для оценивания положений центров кластеров могут быть использованы методы, принадлежащие к любой из трех групп, рассмотренных в подразделе 1.4., предназначенные для оценивания дисперсии аддитивных помех. Это открывает широкие возможности в плане повышения точности оценивания дисперсии сложных помех в рамках вписывания по предварительно выделенным ОТ.

3) В плане обеспечения робастности более перспективным представляется подход, подразумевающий предварительное выделение ОТ с использованием робастной процедуры с последующим вписыванием по ним регрессионной прямой также с использованием робастных методов (РОТРВ).

4) в рамках подхода РОТРВ возникает ряд вопросов, поиск ответов на которые требует проведения многочисленных исследований:

а) каким образом следует получать ОТ?

б) как учесть неодинаковую точность полученных опорных точек?

в) какой метод вписывания следует использовать? и др.

В принципе, скаттерограммный подход может использоваться не только для оценивания характеристик сложных помех, но и для оценивания характеристик чисто сигнально-зависимых (мультипликативных или пуасоновских) или чисто аддитивных помех. В случаях, когда на изображении присутствует только мультипликативный или только пуассоновский шум в скаттерограмму локальных оценок дисперсии и среднего (или его квадрата) осуществляется вписывание регрессионной прямой, выходящей из начала координат. Если же на изображении присутствует только аддитивный шум, то производится вписывание полинома нулевого порядка (прямой, параллельной оси абсцисс).

Что касается ситуации, когда наряду с другими типами шума на изображении присутствует импульсный шум (модель (1.2)), то в рамках скаттерограммного подхода, который наиболее часто используется при оценивании дисперсии сигнально-зависимых и смешанных помех, для обеспечения приемлемой точности оценивания в присутствие импульсных помех необходимо обеспечить робастность вписывания регрессионного полинома. Как уже говорилось, в плане обеспечения робастности вписывания, наиболее перспективным представляется подход РОТРВ, в рамках которого для определения ОТ могут быть использованы различные методы оценивания дисперсии аддитивного шума. Таким образом, если обеспечить приемлемую точность оценивания дисперсии для случая, когда на изображении присутствует смесь аддитивного и импульсного шума (модель (1.9)), то задачу обеспечения требуемой робастности в узком смысле можно будет считать решенной и для сигнально-зависисмых и смешанных помех.

Следует отметить, что тенденция к использованию более сложных моделей помех наметилась относительно недавно, поэтому количество разработанных к настоящему времени методов, предназначенных для оценивания характеристик помех смешанного типа невелико [53 – 56], к тому же точность таких методов, как правило, ниже по сравнению, с методами, предназначенными для оценивания дисперсии одного типа шума. Для методов оценивания характеристик сложных помех сохраняются общие тенденции, описанные в подразделе 1.4. Так, методы оценивания дисперсии смешанных помех, работающие в пространственной и спектральной областях, как правило, обладают высоким быстродействием, однако обеспечивают существенно завышенные оценки дисперсии помех для высокотекстурных изображений [53, 54, 56]. Методы на базе оценивания максимального правдоподобия характеристик шума и изображения обеспечивают более высокую точность оценивания, однако при этом демонстрируют неприемлемо низкое быстродействие [55]. Поскольку на сегодняшний день компромисс между высокой точностью и приемлемым быстродействием используемых методов оценивания характеристик сложных помех не достигнут, остаются актуальными задачи усовершенствования существующих и разработки новых методов в этой области.

Постановка задачи

Несмотря на большое количество разработанных методов автоматического оценивания дисперсии помех, на сегодняшний день нерешенным по-прежнему остается ряд задач.

В первую очередь, это точность оценивания дисперсии помех для изображений со сложной структурой (высокотекстурных). Как уже говорилось в подразделе 1.4, методы, работающие в пространственной области, при работе с такими изображениями обеспечивают существенно завышенные оценки дисперсии в силу негативного влияния информационной составляющей изображения. Несколько лучших результатов удается достичь при использовании методов, работающих в спектральной области, однако поскольку информация, соответствующая текстуре, так же, как и информация, соответствующая шуму, концентрируется в высокочастотных спектральных коэффициентах, для изображений с очень высоким содержанием текстуры успешно разделить помехи и полезную информацию не удается. В результате, оценки дисперсии для этих изображений также оказываются существенно завышенными. Методы третьей группы в большинстве ситуаций способны обеспечивать оценки дисперсии помех для текстурных изображений в пределах требуемой точности, однако в силу неприемлемо низкого быстродействия таких методов, их практическое использование существенно ограничено. В связи с этим, возникает задача усовершенствования методов, работающих в пространственной и спектральной областях, с целью повышения их точности при работе с текстурными изображениями.

Основные направления усовершенствования видятся в использовании предварительной сегментации изображений для частичного устранения аномальных локальных оценок, а также в применении робастных процедур совместной обработки полученных оценок для уменьшения влияния оставшихся аномальных оценок на конечный результат. Перспективным представляется также параллельное оценивание дисперсии в пространственной и спектральной областях с последующим объединением полученной информации.

Ранее отмечалось, что одним из основных недостатков методов, работающих в спектральной области, является их непригодность для работы в условиях воздействия пространственно-коррелированных помех. В связи с этим, с одной стороны, возникает задача разработки методов определения наличия и/или уровня пространственной коррелированности помех и, с другой стороны, задача модификации методов, работающих в спектральной области для обеспечения их работоспособности при оценивании дисперсии пространственно-коррелированных помех.

Несмотря на то, что большинство существующих методов оценивания разработано в предположении, что импульсный шум на обрабатываемых изображениях отсутствует или предварительно устранен, зачастую такие помехи на изображениях присутствуют, причем вероятность их появления априорно неизвестна [57]. Тем не менее, при работе с такими изображениями метод оценивания должен обеспечивать приемлемую точность полученных оценок. В связи с этим, возникает задача модификации методов оценивания дисперсии помех с целью обеспечения их работоспособности в условиях воздействия импульсного шума. Для методов, работающих в пространственной области, перспективным в этом плане представляется использование робастных оценок масштаба.

Следует также отметить, что, несмотря на то, что большинство методов оценивания базируются на изначальном предположении о том, что шум аддитивный с пространственно-инвариантной (постоянной) дисперсией, и во многих фундаментальных работах (например, [58]) утверждается, что такая модель типична для шума на цветных изображениях – это всего лишь упрощенная модель. Вследствие применения операций, проводимых над выходными данными систем формирования изображений, статистические характеристики шума могут быть достаточно сложными [36, 59, 60]. В связи с этим использование автоматических методов оценивания дисперсии, адаптированных под аддитивный шум для анализа реальных изображений, может привести к неожиданным и труднообъяснимым результатам.

В последнее время наметилась тенденция к использованию более сложных моделей помех. В частности, шум на радиолокационных изображениях предлагается рассматривать не как чисто мультипликативный (модель (1.5)), а как смесь аддитивного и мультипликативного шума (модель 1.4). Для описания шума на изображениях, полученных СФИ оптического диапазона, предлагается использовать модель (1.6), то есть рассматривать его как смесь аддитивного и пуассоновского шумов. На сегодняшний день уже существуют методы, предназначенные для оценивания характеристик помех смешанного типа [53 – 56], однако их количество невелико, а точность, как правило, ниже по сравнению, с методами оценивания, ориентированными на какой-то один тип шума.

Важно заметить, что на сегодняшний день не существует единых требований к точности методов оценивания дисперсии сложных помех, что существенно усложняет анализ результатов и принятие решений о пригодности либо непригодности полученных оценок для дальнейшего использования. Отсутствие диапазонов допустимых значений оценок характеристик компонент смешанных помех также в значительной степени усложняет проведение сравнительного анализа результатов, полученных при использовании различных методов.

В связи с этим возникает две задачи. Во-первых, обоснование требований к необходимой точности оценивания характеристик смешанных помех. Во-вторых, усовершенствование методов оценивания сложных помех, направленное на повышение точности получаемых оценок.