Эффективные технологии их отыскания

В отличие от задач обоснования решений по скалярному критерию, результатом решения которых является оптимальная в рамках соответствующей модели альтернатива, в задачах с векторным критерием нельзя с абсолютной уверенностью утверждать, что то или иное решение действительно (объективно) оптимально. Один из вариантов решения может превосходить другой по одним критериям и уступать по другим (другому) критериям. Следовательно, объективно утверждать, что какое-то из двух решений в указанных условиях лучше другого, не представляется возможным. Только со временем будет объективно ясно, сколь верным было принятое решение, Пока же, т. Е. до реализации решения, до оценки его фактической эффективности, личные предпочтения ЛПР, его опыт и интуиция являются единственной основой, которые хоть как-то помогают ему предвидеть последствия принятого компромиссного (по значениям частных критериев) решения. Невозможно строго математически доказать, что выбранное решение наилучшее – любое решение из числа недоминируемых, т.е. неулучшаемых одновременно по всем частным критериям, может оказаться наилучшим для конкретного ЛПР в конкретных условиях. Таким образом, сложность проблемы принятия решений по векторному критерию даже в условиях определенности связана не столько с вычислительными трудностями, сколько с концептуальной обоснованностью выбора «оптимального» решения.

Сравнения альтернатив по векторному критерию прежде всего будем осуществлять по следующему очевидному правилу: высокая альтернатива критерия не менее предпочтительнее любой другой, если для нее значение векторного значения критерия не хуже, чум е другой альтернативы, т.е.

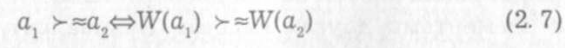
Где а₁,а₂ – альтернативы;

W(a) – векторный критерий;

ý» – символ отношения нестрогого предпочтения.

В выражении (2.7) словосочетание «отношение нестрогого предпочтения» следует понимать в математическом смысле[6]. Означает она в этом смысле нестрогое упорядочение, заданное на элементах какого-то множества. Наиболее употребительными в математической теории принятия решений являются бинарные отношения, так как они легко интерпретируются и достаточно просто выявляются традиционными способами выражения элементарных суждений[6].

Для математического моделирования предпочтений всегда важно знать, какими из свойств бинарных отношений оно обладает. Среди разнообразных свойств бинарных отношений нас прежде всего будет интересовать такие, как рефлексивность, симметричность, транзитивность и связность (полнота), поскольку именно они во многом определяют разрешающую способность модели — способность точно предсказывать истинные предпочтения и выборы ЛПР. Если перечисленные свойства у бинарного отношения, моделирующего предпочтения ЛПР, в той или иной степени отсутствуют, этот факт будем отмечать указанием на нерефлексивность, несимметричность, несвязность, вплоть до их полной противоположности, а именно: антирефлексивности, антисимметричности и т. п.

В частности, бинарное отношение называют эквивалентностью, если оно обладает свойствами рефлексивности, транзитивности и симметричности. Это отношение играет важную роль при принятии решений, поскольку моделирует факт разбиения множества предъявленных ЛПР элементов на определенные классы одинаковой предпочтительности. Элементы, принадлежащие одному классу эквивалентности, равноценны по предпочтению, а принадлежащие разным классам — резко различаются по предпочтительности при их сравнении с элементами других классов. Эквивалентность между элементами можно понимать как их взаимозаменимость при выборе для ЛПР. При этом свойство транзитивности очень важно для однозначности отнесения объекта к тому или иному классу. Если отношение предпочтения только лишь симметрично и рефлексивно, то оно будет толерантностью (образовывать класс "похожих" элементов), но не эквивалентностью. Так, например, результаты сортировки в ходе экспертизы могут моделироваться либо как эквивалентность, либо как толерантность — в зависимости от степени уверенности, с которой ЛПР сортировало множество предъявления в соответствии со своими предпочтениями. Обычно ЛПР среди предъявленных ему элементов может уверенно отнести к тому или иному классу лишь элементы субъективно "сильно" различающиеся между собой, а среди оставшихся, "похожих", действует менее уверенно. В результате транзитивность на границах между классами может нарушаться, а выявленное отношение предпочтения моделируется лишь рефлексивным и симметричным бинарным отношением, которое и представляет собой толерантность.

Бинарное отношение называют строгим порядком, если оно транзитивно и строго антисимметрично. С его помощью моделируют отношение строгого предпочтения ЛПР. Примером отношения строгого порядка является отношение "меньше" на множестве действительных чисел. Если же бинарное отношение помимо свойств транзитивности и антисимметричности обладает еще и рефлексивностью, то это — квазипорядок ("почти порядок"). Например, результаты попарного сравнения каких-то элементов в ходе экспертизы в общем случае могут оказаться как рефлексивными, так и антирефлексивными, поскольку сравнение элементов производится только в парах, т. е. без учета остальных элементов. Это может привести к тому, что свойство транзитивности на множестве всех элементов может отсутствовать. Ранжирование элементов — это также один из распространенных способов выявления элементарных суждений в ходе экспертизы. Так вот, оно в общем случае задает отношение квазипорядка на множестве всех элементов, поскольку разрешается разные элементы располагать на одном месте в упорядоченном ряду.

А вот если этого делать не разрешено, если ранжирование так называемое строгое, то при строгом ранжировании моделируемое отношение предпочтения будет отношением строгого порядка. Результаты же балльного оценивания, а также результаты выражения предпочтения субъективными вероятностями или коэффициентами важности устанавливают отношение связного квазипорядка. Из всего сказанного следует, что наиболее серьезными недостатками моделей предпочтения, вскрытыми в ходе экспертизы с использованием элементарных суждений, является отсутствие свойств транзитивности и связности. Именно это зачастую затрудняет анализ истинных предпочтений ЛПР.

Понимая это, указанные недостатки моделей предпочтений всячески стараются избежать, специально организуя экспертизу, объединяя ее с математическими методами проверки, анализа и повышения достоверности суждений. В результате простая экспертиза превращается в сложный процесс — процесс экспертного оценивания.

Если в процессе экспертного оценивания установлено, что на множестве оценок ю критерия W предпочтения ЛПР транзитивные, связные и непрерывные, то каждый исход операции можно оценить по предпочтительности с помощью функции ценности v(w). Для задач обоснования решений в условиях определенности эта функция является частным случаем функции и(а) полезности. Доказано[4] , что функция ценности существует всегда, когда ЛПР считает, что для любой оценки w уменьшение значений одних компонент wi может быть компенсировано увеличением значений других компонент w. так, что исходная оценка w и новая оценка wy оказываются одинаково предпочтительными. Говорят, что в таком случае предпочтения ЛПР плавные, что не изменяются резко, скачком. Функция ценности задает весьма совершенную модель предпочтения, которая обладает свойствами связного квазипорядка. Если функция ценности построена, значит перед вами самый короткий путь для решения задачи выбора наилучшей альтернативы: выбирайте ту альтернативу, у которой измеренная с помощью этой функции ценность наибольшая.

Однако подчас необходимые для построения функции ценности знания в области ТПР, умения и навыки у ЛПР отсутствуют, а требуемые для совершения этой работы активные ресурсы — время, деньги, специальное математическое обеспечение и т. п. — отсутствуют в нужных количествах. Да ведь и не все проблемы, возникающие перед ЛПР, на практике оказываются столь важными, чтобы обязательно как можно более точно моделировать его предпочтения.

Как тут быть? Во всех перечисленных случаях для отыскания наилучшей альтернативы ТПР рекомендует ЛПР следовать принципу Родена. Когда у этого великого скульптора спросили, как ему удается создавать столь великие шедевры, Роден ответил: "Я просто беру глыбу мрамора и отсекаю от нее все лишнее!"

Прекрасная идея: последовательно отсекайте от множества альтернатив все элементы, которые "не нужны", которые являются "лишними", а то, что останется (не лишнее), — это и есть то, что вам нужно — наилучшая альтернатива (или несколько эквивалентных по предпочтительности наилучших альтернатив). Концептуальную идею, изложенную в вербальной форме Роденом, реализовал в формальном виде и превратил в одну из наиболее эффективных функций выбора видный социолог и экономист В. Парето (вспомните, ему же принадлежало и известное нам правило "20/80"). Парето ввел понятие взаимной независимости частных критериев по предпочтительности и на основе этого сформулировал известную аксиому о доминируемости. Рассмотрим это понятие и эту аксиому. При этом везде далее будем полагать, что для ЛПР большие значения каждого из частных критериев предпочтительнее меньших значений. Задачи обоснования решений с такими направлениями предпочтений по всем критериям будем называть положительно ориентированными (по предпочтениям).

Подумаем вот над каким вопросом: могут ли измениться направления предпочтений по каким-то из критериев в зависимости от того, какие в этот момент приняли значения другие критерии? Вопрос этот не праздный. Оказывается, что если число т частных критериев больше двух, то направления предпочтения по одним критериям могут измениться в зависимости от того, какие значения принимают другие критерии. Такая ситуация наблюдается, если ЛПР считает необходимым "выдержать пропорцию" между значениями критериев, придать их значениям некую определенную им гармоничность.

Например, гармоничными должны быть размеры концертного зала филармонии для обеспечения выразительного звучания оркестра, гармоничными должны быть характеристики экспансии товаров на рынке сбыта, чтобы уровень сервиса при продаже, качество гарантийного и послегарантийного обслуживания отвечали заявленным в рекламе при разумных уровнях затрат на них. Везде в ситуациях разработки решений, подобных описанным в примерах, может измениться направление предпочтения по одному или нескольким частным критериям в зависимости от того, какие значения приобрели другие критерии.

Если же направление предпочтения по какому-либо критерию не изменяется с изменением значений других критериев, то такой критерий будем называть независимым по предпочтению от остальных. Следует сказать, что на практике довольно часто оказывается, что, по мнению ЛПР, каждый критерий является независимым по предпочтению от остальных. Такую ситуацию с предпочтениями ЛПР будем характеризовать словами "взаимная зависимость частных критериев по предпочтению".

Аксиома Парето (принцип доминирования).

Если частные критерии W взаимно независимы по предпочтению, то из двух векторных оценок w(а),w (b), для которых выполняются неравенства

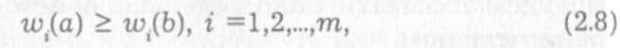
векторная оценка w(а)не менее предпочтительна оценки w(b). При этом если хотя бы одно из указанных нестрогих неравенств выполняется как строгое, то оценка w(а) доминирует над оценкой w(b).

Будем обозначать любую информацию о предпочтениях, на основе которой построена модель предпочтения ЛПР, с помощью аббревиатуры inf. Для уточнения типа модели предпочтения и того, на основе какой конкретно информации эта модель построена, будем использовать различные аббревиатуры. Так, информацию о предпочтениях ЛПР, содержащую сведения о взаимной независимости критериев по предпочтительности, будем обозначать аббревиатурой iop (от англ. independence оf preference). Если inf = iор, то из исходного множества вариантов решений как раз и можно выделить так называемые недоминируемые (их еще называют эффективиые, нехудшие, неулучшаемые одновременно по всем критериям) альтернативы. С учетом этих обозначений краткую формальную запись факта доминирования альтернативы а над альтернативой b запишем так:

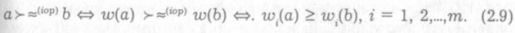
Если все неравенства в выражении (2.9) выполняются как равенства, то альтернативы а и b эквивалентны (символ ») по предпочтительности. Формальная запись такого факта имеет вид

а»^(iop) b.

Отношения (2.8) и (2.9) не являются связными, так как для произвольных векторных оценокwю(а), w(b) часть неравенств (2.8) может выполняться "в одну сторону", (т. е. w_i (а) ³w_i(b)), а остальные — "в другую сторону" (w_j (а)≤ w_j(b)). Такие векторные оценки оказываются несравнимыми по Парето и образуют множество недоминируемых оценок, которым соответствует множество недоминируемых (эффективных по Парето) альтернатив. Таким образом, отличительной особенностью недоминируемых или эффективных по Парето альтернатив является то, что ни у одной из них ни по одному из их частных критериев оценка не может быть улучшена без ухудшения оценки какого-то другого (или других) критерия. Следовательно, эффективные альтернативы между собой несравнимы, и на множестве значений векторных оценок можно определить результат применения функции выбора. Этот результат применения функции выбора на множестве значений векторных оценок будем называть ядром отношения по заданной информации о предпочтениях ЛПР и обозначать eff(w,inf). Таким образом, ядро отношения Парето получит обозначение ef f(w,iop). Для задач с положительно ориентированными критериями ядро eff(w,iop) отношения Парето расположено в северо-восточном направлении на границе достижимого множества векторных оценок. При этом мощность множества оценок ядра может быть различной в зависимости от конкретных особенностей (в частности, конфигурации) достижимого множества оценок. На рис. 2.6 представлены различные возможны е конфигурации множества eff{w,iop) для двумерных векторных оценок.

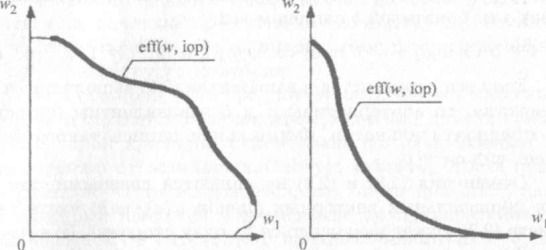
Рис. 2.6. Возможные конфигурации множества

Конфигурация допустимого множества векторных оценок, представленного на рис. 2.6, а, такова, что ядро занимает лишь часть северо-восточной границы этого множества, а на рис. 2.6, б ядро занимает всю северо-восточную границу.

Но практически всегда эффективные альтернативы составляют лишь часть исходного множества альтернатив. Это, естественно, упрощает поиск наилучшего решения, так как совершенно ясно, что решение может считаться наилучшим только тогда, когда оно эффективно. Другими словами, наилучшее решение не может быть неэффективным.

Если для каждой альтернативы уже получены оценки частных критериев, поиск эффективного ядра, как правило, не вызывает затруднений. Технология здесь предельно проста:

1) выбрать какую-то альтернативу;

2) включить ее во множество недоминируемых;

3) взять очередную альтернативу из исходного множества; назовем ее "претендент";

4) проверить, не доминируется ли "претендент" альтернативой из множества недоминируемых; если "претендент" не доминируется, то проверить, не доминирует ли он над первой; если "претендент" доминирует, исключить первую альтернативу из числа недоминируемых , а " претендента " включить в число недоминируемых, иначе — "претендента" также включить в число недоминируемых;

5) если среди альтернатив исходного множества осталась хотя бы одна еще не проверенная на эффективность, назначить ее "претендентом", иначе — " Stop ";

6) последовательно проверять, не доминируется ли " претендент " какой-либо из альтернатив, уже включенных во множество недоминируемых; при первом же обнаружении факта доминирования над "претендентом" его из дальнейшего анализа исключить и перейти к шагу 5;

7) последовательно проверять, не доминирует ли " претендент" над какой-то из альтернатив, ранее уже включенных во множество недоминируемых; если окажется, что " претендент" доминирует над какой-то из альтернатив, уже включенных во множество недоминируемых, э т у альтернативу из множества недоминируемых исключить;

8) перейти к шагу 5;

9) " Stop " .

Как было показано автором[2], данный алгоритм значительно выгоднее по числу сравнений, которые потребуется провести, чтобы найти эффективное ядро, чем прямое и с пользование правила (2.9).

Если же нет данных о значениях оценок критерия [6] W(a) для альтернатив а ? А, а эти оценки могут быть получены, если предварительно формально задать описание альтернатива G А через некоторые их характеристики х е X, то задача построения эффективного ядра существенно усложняется.

Здесь приходится специальным образом организовать зондирование пространства X характеристик альтернатив, для каждой получаемой точки х е X, отражающей а £ А, вычислять W(a), а затем у ж е решать вопрос о доминировании. Что бы придать указанному процессу логическую направленность, в общем то, вновь обращаются к соотношению (2.9), но технологически его интерпретируют по-разному. Рассмотрим наиболее распространенные технологии отыскания эффективных альтернатив по методу зондирования пространства характеристик и графически проиллюстрируем их смысл для двумерного случая векторного критерия.

Технология, основанная на использовании теоремы Гермейера, пригодна для случая, когда все частные показатели имеют положительные оценки, т. е. все w_i > 0. Технология предполагает назначение в качестве "уровней притязаний" в правой части выражения (2.8) минимальных значений w_i для "претендента", а поиск эффективной альтернативы вести по направлениям от начала координат в сторону возрастания значений каждого из частных критериев. Если оценку "претендента" обозначить через х₀,а на правление λ поиска эффективной альтернативы задать, например, как λ_i = q/x_0i, то максимум функции

будет достигаться на эффективной альтернативе, принадлежащей ядру. Графиком функции min {λi*w_i(а)} является прямой угол, стороны которого параллельны осям w_i координат в пространстве оценок векторного критерия. Следовательно, все значения критерия, которые имеют хотя 6ы одну из частных компонентов лучше, чем "претендент", геометрически будут точками, принадлежащими северо-восточной подобласти в направлении от границ этого прямого угла. Максимизации функции Гермейера min {λ_i*w_i (а)} по множеству альтернатив обязательно приведет к множеству eff(w, iop), т. е. к эффективной границе.

Однако функция Гермейера не очень удобна для оптимизации. Поэтому второй часто используемой технологией поиска эффективных альтернатив является процесс, основанный на применении классического метода гласного показателя. Позже мы этот метод разберем подробнее, а пока нужно знать только то, что, согласно этому подходу, в выражении (2.8) для всех частных критериев, кроме одного, назначаются уровни с_j притязаний. Оставшийся критерий назначается "главным" и он максимизируется при наложенных ограничениях на остальные. Например, главным назначим критерий w_i и решим задачу вида:

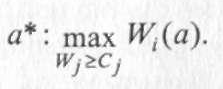
Получаемая в результате оптимизации альтернатива со значением w* векторного критерия будет эффективной. Еще более простой в применении оказывается технология, предполагающая максимизацию не одного, «главного» частного критерия, а линейной свертки от всех критериев. Эта технология построена на результатах теоремы, доказанной тремя учеными - Куном, Таккером и Карлиным. Было показано, что если множество альтернатив, задаваемых характеристиками х, выпукло, а все w_i(а) - вогнуты, то для всякой эффективной стратегии а^о найдутся такие неотрицательные числа у_i, в сумме равные единице, что

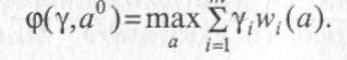
Ясно, что требование вогнутости w_i(а) и выпуклости W существенны, поскольку иначе не все эффективные альтернативы, а именно те, векторные оценки которых принадлежат вогнутой части эффективной границы, не смогут быть выделены по этой технологии ни при каких величинах весовых коэффициентов y_i.

Соответствующие представленным технологиям графические иллюстрации представлены на рис. 2.7. На рис. 2.7, а показано, что любая альтернатива а Î А задается набором характеристик в пространстве Х, а также отмечен "претендент" х₀. На рис. 2.7, б заштрихованной областью показано множество векторных оценок w(х), доминируощих над рассматриваемым "претендентом" с оценкой w(х₀). 3а этом же рисунке штрихпунктирными стрелками показаны направления λ поиска очередной эффективной точки на северо-восточной границе множества оценок по методу Гермера,

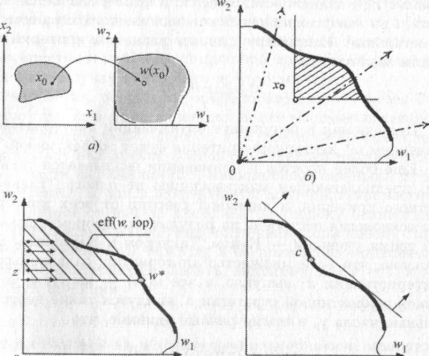
Рис. 2.7. Графическая иллюстрация технологий зондирования

а на рис. 2.7, в проиллюстрирована суть технологии по методу главного показателя. Рис. 2.7, г помогает понять, почему требование выпуклости достижимого множества векторных оценок, фигурирующее в теореме Куна-Таккера-Карлина, весьма существенно. На этом рисунке изображена линия уровня

в виде прямой, для линии уровня стрелками показано направление возрастания ее значений (направление градиента). Когда указанная функция достигает максимума при заданных значениях коэффициентов y, прямая ф(у, а) = const занимает положение касательной к границе еff(w, iop). Из рис. 2.7, г видно, что точка с, лежащая на вогнутой части аффективной границы, действительно не достижима ни при каких значениях параметров у рассматриваемой линейной сверки оценок критериев.

Итак, множество эффективных альтернатив не шире исходного множества, а подчас существенно уже его. Но все же ядро eff(w, iop) отношения Парето может включать достаточно большое число элементов. И это обстоятельство не позволяет сразу осуществить выбор наилучшего решения. Например, установлено, что для двумерного дискретного множества достижимых векторных оценок, состоящего из N независимо сгенерированных альтернатив, математическое ожидание числа элементов ядра отношения Парето стремится к величине In N. Как мы уже знаем, все эти альтернативы не сравнимы. Для дальнейшего выбора лучшей из них необходимо привлечь дополнительную информацию о предпочтениях ЛПР. Такой дополнительной информацией могут служить сведения о6 относительной важности частных критериев. Соизмеряя степень влияния изменения значений одном из критериев по сравнению с изменением значений другого (других), ЛПР может установить относительную важность частных критериев.

Пример:

Решение о вложении нераспределенной прибыли в ценные бумаги государства. В данном случае менеджер точно знает размер вкладываемой суммы, может выбрать сроки вложения, рассчитать доходность и может точно подсчитать планируемую прибыль от данного вложения и сроки ее получения. Государство может не выполнить свои обязательства только при возникновении чрезвычайных обстоятельств, вероятность возникновения которых очень мала. Однако в условиях, сложившихся на данный момент в нашей республике, данный пример отражает меньший уровень определенности, чем в развитых странах. В странах с развитой стабильной экономикой менеджер может также точно рассчитать затраты на производство определенного вида зделий на ближайшую перспективу. Это возможно, потому что постоянные издержки, стоимость материалов и рабочей силы известны или могут быть рассчитаны с высокой степенью точности.