Математическое обеспечение анализа на системном уровне
Объектами проектирования на системном уровне являются такие сложные системы, как производственные предприятия, транспортные системы, вычислительные системы и сети, автоматизированные системы проектирования и управления и т.п. В этих приложениях анализ процессов функционирования систем связан с исследованием прохождения через систему потока заявок (иначе называемых требованиямиили транзактами). Разработчиков подобных сложных систем интересуют прежде всего такие параметры, как производительность (пропускная способность) проектируемой системы, продолжительность обслуживания (задержки) заявок в системе, эффективность используемого в системе оборудования.
Заявками могут быть заказы на производство изделий, задачи, решаемые в вычислительной системе, клиенты в банках, грузы, поступающие на транспортировку и др. Очевидно, что параметры заявок, поступающих в систему, являются случайными величинами и при проектировании могут быть
известны лишь их законы распределения и числовые характеристики этих распределений. Поэтому анализ функционирования на системном уровне, как правило, носит статистический характер. В качестве математического аппарата моделирования удобно принять теорию массового обслуживания, а в качестве моделей систем на этом уровне использовать системы массового обслуживания (СМО).
Типичными выходными параметрами в СМО являются числовые характеристики таких величин, как время обслуживания заявок в системе, длины очередей заявок на входах, время ожидания обслуживания в очередях, загрузка устройств системы, а также вероятность обслуживания в заданные сроки и т.п.
В простейшем случае СМО представляет собой некоторое средство (устройство), называемое обслуживающим аппаратом (ОА), вместе с очередями заявок на входах. Более сложные СМО состоят из многих взаимосвязанных ОА. Обслуживающие аппараты СМО в совокупности образуют статические объектыСМО, иначе называемые ресурсами. Например, в вычислительных сетях ресурсы представлены аппаратными и программными средствами.
В СМО, кроме статических объектов, фигурируют динамические объекты — транзакты. Например, в вычислительных сетях динамическими объектами являются решаемые задачи и запросы на информационные услуги. Состояние СМО характеризуется состояниями составляющих ее объектов. Например, состояния ОА выражаются булевыми величинами, значения которых интерпретируются как true (занято) и false (свободно), и длинами очередей на входах ОА, принимающими неотрицательные целочисленные значения. Переменные, характеризующие состояние СМО, будем называть переменными состояния или фазовыми переменными.
Правило, согласно которому заявки выбирают из очередей на обслуживание, называют дисциплиной обслуживания, а величину, выражающую преимущественное право на обслуживание, — приоритетом. В приоритетных дисциплинах, все транзакты имеют одинаковые приоритеты. Среди бесприоритетных дисциплин наиболее популярны дисциплины FIFO (первым пришел — первым обслужен), LIFO (последним пришел — первым обслужен) и со случайным выбором заявок из очередей.
В приоритетных дисциплинахдля заявок каждого приоритета на входе ОА выделяется своя очередь. Заявка из очереди с низким приоритетом поступает на обслуживание, если пусты очереди с более высокими приоритетами. Различают приоритеты абсолютные, относительные и динамические.
Заявка из очереди с более высоким абсолютным приоритетом, поступая на вход занятого ОА, прерывает уже начатое обслуживание заявки более низкого приоритета. В случае относительного приоритета прерывания не происходит, более высокоприоритетная заявка ждет окончания уже начатого обслуживания. Динамические приоритеты могут изменяться во время нахождения заявки в СМО.
Исследование поведения СМО, т.е. определение временных зависимостей переменных, характеризующих состояние СМО, при подаче на входы любых требуемых в соответствии с заданием на эксперимент потоков заявок, называют имитационным моделированием СМО. Имитационное моделирование проводят путем воспроизведения событий, происходящих одновременно или последовательно
в модельном времени. При этом под событием понимают факт изменения значения любой фазовой переменной.
Подход, альтернативный имитационному моделированию, называют аналитическим исследованием СМО. Аналитическое исследование заключается в получении формул для расчета выходных параметров СМО с последующей подстановкой значений аргументов в эти формулы в каждом отдельном эксперименте.
Модели СМО, используемые при имитационном и аналитическом моделировании, называются имитационными и аналитическими соответственно.
Аналитические модели удобны в использовании, поскольку для аналитического моделирования не требуются сколько-нибудь значительные затраты вычислительных ресурсов, часто без постановки специальных вычислительных экспериментов разработчик может оценить характер влияния аргументов на выходные параметры, выявить те или иные общие закономерности в поведении системы. Но, к сожалению, аналитическое исследование удается реализовать только для частных случаев сравнительно несложных СМО. Для сложных СМО аналитические модели если и удается получить, то только при принятии упрощающих допущений, ставящих под сомнение адекватность модели.
Поэтому основным подходом к анализу САПР на системном уровне проектирования считают имитационное моделирование, а аналитическое исследование используют при предварительной оценке различных предлагаемых вариантов систем.
Некоторые компоненты СМО характеризуются более чем одним входным и (или) выходным потоками заявок. Правила выбора одного из возможных направлений движения заявок входят в соответствующие модели компонентов. В одних случаях такие правила относятся к исходным данным (например, выбор направления по вероятности), но в некоторых случаях желательно найти оптимальное управление потоками в узлах разветвления. Тогда задача моделирования становится более сложной задачей синтеза, характерными примерами являются маршрутизация заявок или синтез расписаний и планов.
Как отмечено выше, аналитические модели СМО удается получить при довольно серьезных допущениях. К числу типичных допущений относятся следующие.
Во-первых, как правило, считают, что в СМО используются бесприоритетные дисциплины обслуживания типа FIFO.
Во-вторых, времена обслуживания заявок в устройствах выбираются в соответствии с экспоненциальным законом распределения.
В-третьих, в аналитических моделях СМО входные потоки заявок аппроксимируются простейшимипотоками, т.е. потоками, обладающими свойствами стационарности, ординарности (невозможности одновременного поступления двух заявок на вход СМО), отсутствия последействия.
Сеть Петри— аппарат для моделирования динамических дискретных систем (преимущественно асинхронных параллельных процессов). Сеть Петри определяется как четверка <P,T,I,O>, где Р и Т—конечные множества позиций и переходов, I и О— множества входных и выходных функций. Другими словами, сеть Петри представляет собой двудольный ориентированный граф, в котором позиции соответствуют вершины, изображаемые кружками, а переходам — вершины, изображаемые утолщенными черточками; функциям Iсоответствуют дуги, направленные от позиций к переходам, а функциям О— от переходов к позициям.
Как и в системах массового обслуживания, в сетях Петри вводятся объекты двух типов: динамические — изображаются метками (маркерами)внутри позиций и статические — им соответствуют вершины сети Петри.
Распределение маркеров по позициям называют маркировкой. Маркеры могут перемещаться в сети. Каждое изменение маркировки называют событием, причем каждое событие связано с определенным переходом. Считается, что события происходят мгновенно и разновременно при выполнении некоторых условий.
Каждому условию в сети Петри соответствует определенная позиция. Совершению события соответствует срабатывание (возбуждение или запуск) перехода, при котором маркеры из входных позиций этого перехода перемещаются в выходные позиции. Последовательность событий образует моделируемый процесс.
Правила срабатывания переходов (рис. 4.7), конкретизируют следующим образом: переход срабатывает, если для каждой из его входных позиций выполняется условие: Ni & Ki, где Ni— число маркеров в i-й входной позиции, Ki— число дуг, идущих от i-й позиции к переходу; при срабатывании перехода число маркеров в i-й входной позиции уменьшается на Ki, а в j-й выходной позиции увеличивается на Mj, где Mj— число дуг, связывающих переход с j-й позицией.
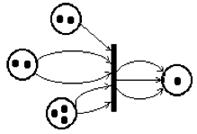
Рис. 4.7 Пример организации перехода в сетях Петри.
Можно вводить ряд дополнительных правил и условий в алгоритмы моделирования, получая ту или иную разновидность сетей Петри. Так, прежде всего полезно ввести модельное время, чтобы моделировать не только последовательность событий, но и их привязку ко времени. Это осуществляется приданием переходам веса — продолжительности (задержки) срабатывания, которую можно определять, используя задаваемый при этом алгоритм. Полученную модель называют временной сетью Петри.
