Метод циклического координатного поиска Гаусса-Зейделя

Метод Гаусса-Зейделя или циклического координатного поиска заключается в том, что на итерациях по каждой переменой определяется минимум целевой функции вдоль направления координатных осей. После чего осуществляется поиск вдоль другой координаты. Поиск по направлениям, совпадающим с координатными осями, можно проводить любым известным методом одномерной оптимизации, например, методом золотого сечения или обратного переменного шага. Таким образом, задача сводится к многократному использованию метода одномерной оптимизации. Очередность варьирования переменных обычно устанавливается произвольно и в процессе поиска не меняется. Точность поиска проверяется по сравнению значений переменных и функции на (k + 1) и (k) итерациях.

Алгоритм метода Гаусса-Зейделя.

Начальный этап. Выбрать начальную точку X⁽¹⁾, и e> 0 - скаляр, используемый в критерии остановки. Пусть 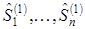единичные координатные направления. Положить Y⁽¹⁾ = X⁽¹⁾, k = j = 1 и перейти к основному этапу.

Основной этап. Шаг 1. Любым методом одномерной оптимизации найти l_j^* - оптимальное решение задачи минимизации функции f(Y^(j) + l_j 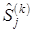) и положить Y^(j+1) = Y^(j) + l_j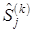^* . Если j < n, то заменить j на j + 1 и вернуться к шагу 1. Если j=n, то перейти к шагу 2.

Шаг 2. Положить X^(k+1) = Y⁽ⁿ⁾. Если ||X^(k+1) - X^(k)|| < e, то остановиться; в противном случае положить Y⁽¹⁾ = X^(k+1), заменить k на k + 1, положить j = 1 и перейти к шагу 1.

Пример расчета экстремума функции методом циклического координатного поиска Гаусса-Зейделя.

Постановка задачи. Определить экстремум функции f(X) = (x₁ - 2)⁴ + (х₁ - 2х₂)² с точностью e=0,01 для начального приближения Х⁽¹⁾=[2.5; 2.5].

Расчет экстремума методом Гаусса-Зейделя для данной задачи реализован средствами EXСEL. Результаты расчета представлены в таблице 2.1. На рисунке 2.1 приведены линии уровня для данной функции и траектория поиска.

Таблица 2.1.

Результаты расчета минимума функции f(x)=(x₁-2)⁴+(х₁-2х₂)² методом Гаусса - Зейделя.

№	x1	x2	f(X)	λ1	λ 2	||X(k+1) - X(k)||	Критерий
	2.500	2.500	6.31250
	3.000	2.500	5.00000	0.500	0.000	1.0000	не достигнут
3.000	1.5000	1.00000	0.000	-1.000
	2.5898	1.5000	0.28927	-0.410	0.000	0.2051	не достигнут
2.5898	1.2949	0.12097	0.000	-0.205
	2.4304	1.2949	0.05971	-0.159	0.000	0.0797	не достигнут
2.4304	1.2152	0.03430	0.000	-0.080
	2.3469	1.2152	0.02145	-0.083	0.000	0.0417	не достигнут
2.3469	1.1734	0.01448	0.000	-0.042
	2.2953	1.1734	0.01026	-0.052	0.000	0.0258	не достигнут
2.2953	1.1477	0.00761	0.000	-0.026
	2.2601	1.1477	0.00582	-0.035	0.000	0.0176	не достигнут
2.2601	1.1301	0.00458	0.000	-0.018
	2.2344	1.1301	0.00368	-0.026	0.000	0.0129	не достигнут
2.2344	1.1172	0.00302	0.000	-0.013
	2.2146	1.1172	0.00251	-0.020	0.000	0.0099	достигнут
2.2146	1.1073	0.00212	0.000	-0.010

Таким образом, после восьми итераций достигнута заданная точность. С такой точностью найдена оптимальная точка Х*=[2.2146; 1.1073]. Следует отметить, что минимум функции находится в точке Х*=[2; 1].

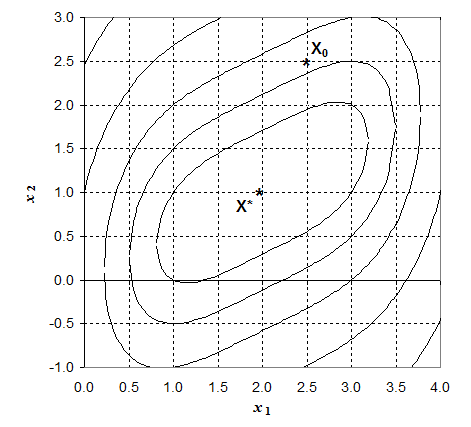Рис.2.1 Графическая иллюстрация поиска экстремума функции методом циклического покоординатного поиска Гаусса Зейделя.