Методы оценивания дисперсии помех в пространственной области

Первая группа является наибольшей по количеству предложенных на данный момент методов оценивания дисперсии помех в пространственной области [24, 27 – 34]. Как видно из дат выхода и названий этих публикаций, интерес к автоматическому оцениванию характеристик помех возник во второй половине 90-х годов прошлого столетия и, в основном, применительно к радиолокационным изображениям.

Методы оценивания в пространственной области базируются на предположении, что блоки определенного размера заполняют изображение и среди них есть набор блоков, принадлежащих однородным участкам. Локальные оценки дисперсии шума для этих блоков достаточно близки к истинному значению дисперсии шума. Путем совместной обработки «нормальных» локальных оценок может быть получено значение результирующей оценки дисперсии.

Основная проблема при использовании методов оценивания в пространственной области заключается в выделении группы «нормальных» оценок, соответствующих однородным участкам изображения, и либо устранении аномальных оценок, соответствующих участкам, содержащим границы и текстуру, либо минимизации влияния аномальных оценок на конечный результат оценивания.

Для решения этих проблем предложены различные подходы, большинство из них в той или иной степени связаны с робастным оцениванием [22, 35]: использованием устойчивого вписывания модельных кривых [32, 33, 36] или применением устойчивых оценок [30, 31, 34, 37 – 39].

На рисунке 1.7 приведена гистограмма локальных оценок для изображения, искаженного аддитивными помехами с дисперсией 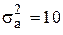. Нормальные оценки формируют моду распределения, координата которой может служить оценкой 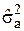, а аномальные оценки формируют длинный правосторонний хвост распределения. Таким образом, для получения оценок 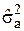должны использоваться методы определения координаты моды таких распределений, что для теории робастного оценивания параметров сдвига

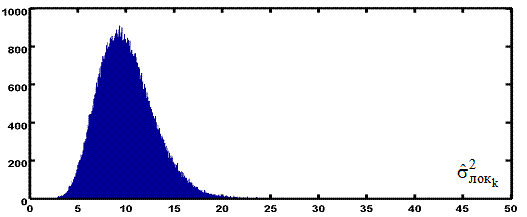Рисунок 1.7 – Фрагмент гистограммы локальных оценок 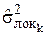(Nбл = 5х5) для аддитивных помех ( )

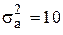распределений не является типичной задачей (более характерной является задача определения параметра сдвига распределений, симметричных относительно математического ожидания или центра распределения для ПРВ с тяжелыми хвостами [39]).

К настоящему времени разработаны эффективные методы оценивания координаты моды распределения локальных оценок дисперсии. Они основываются на использовании мириадной оценки с адаптивно выбираемым параметром 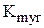[31], применении бутстреппирования [40], интерквантильных расстояний [37, 38]. Эти методы позволяют оценить относительное количество нормальных оценок локальной дисперсии:

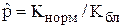, (1.20)

где 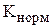- количество нормальных оценок дисперсии;

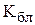- общее количество блоков (скользящих окон) на изображении.

По значению 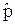можно определить степень текстурности изображения (текстурными можно условно считать изображения, для которых значение ).

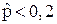Одним из направлений повышения точности оценивания координаты моды распределения локальных оценок дисперсии является использование предварительной обработки, например, сегментации изображений с целью устранения значительной части аномальных локальных оценок дисперсии [24, 37]. В этом плане, наиболее привлекательным является метод сегментации [41], поскольку он работоспособен при отсутствии априорной информации о типе и характеристиках помех.

Для обеспечения слабой зависимости точности оценивания от пространственно-корреляционных свойств помех обоснована необходимость использования блоков большего размера (7х7 или 9х9 пикселей) [37].

Одним из наиболее эффективных среди методов оценивания, работающих в пространственной области, является метод [37], предназначенный для оценивания дисперсии аддитивного либо относительной дисперсии мультипликативного шума. Для большинства изображений при стандартном 8-битном представлении и характерных дисперсиях 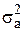порядка 50...200 или 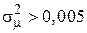метод [37] обеспечивает приемлемую точность оценивания, если 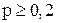и размер изображения 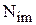составляет десятки тысяч пикселей. Общие закономерности состоят в следующем [37]:

а) точность, характеризуемая наиболее общими показателям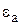и или 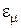, повышается при увеличени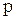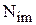и , и 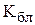; первые два параметра не зависят от пользователя, а 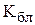может быть увеличен благодаря использованию перекрытия блоков, если позволяют временные ограничения;

б) для изображений с 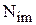порядка сотен тысяч пикселей больший вклад в 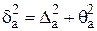и 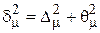вносят первые слагаемые, поэтому относительные погрешност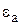и и 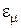определяются, прежде всего, смещенностью оценок; следовательно, основное внимание необходимо уделять уменьшению абсолютных значений смещенности;

в) смещенности, как правило, являются положительными, то есть оценки дисперсии оказываются завышенными; это вызвано влиянием информационной составляющей обрабатываемых изображений;

г) чем меньше значения 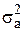или 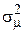, тем ниже точность их оценивания (больше значения 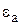или 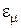соответственно), что также обусловлено более высоким негативным влиянием информационной составляющей изображений;

д) для тестовых незашумленных изображений, которые в мировой практике тестирования и сравнительного анализа эффективности обработки используются в качестве эталонов (Lena, Barbara, Peppers, Goldhill, Boat, Baboon (приведены на рисунке 1.8)), получаемые оценки 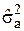имеют порядок от 3 до 10 (за исключением тестового изображения Baboon, для которого оценка 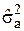равна 25), что одновременно свидетельствует о присутствии небольшого шума на этих тестовых изображениях, отсутствии на них идеально однородных участков и принципиальных ограничениях точности методов автоматического оценивания характеристик помех в пространственной области при малом уровне помех, особенно для текстурных изображений.

На примере метода [37] хорошо видны основные достоинства и недостатки методов оценивания дисперсии помех в пространственной области. К достоинствам методов из этой группы следует отнести следующее:

а	б	в
г	д	е
Рисунок 1.8 – Тестовые незашумленные изображения: Lena (a), Barbara (б), Peppers (в), Goldhill (г), Boat (д), Baboon (е)

1) возможность обеспечения независимости точности оценивания от пространственно-корреляционных свойств помех при правильном выборе параметров (в частности, размеров используемых блоков);

2) относительная простота реализации;

3) высокое быстродействие.

Среди недостатков методов оценивания, принадлежащих к этой группе, следует отметить:

1) существенное завышение оценок дисперсии для изображений с высоким содержанием текстур, границ и малоразмерных объектов;

2) принципиальные ограничения точности оценивания при малом уровне искажающих помех.

1.4.2 Методы оценивания дисперсии помех в спектральной области

В основе большинства методов, работающих в спектральной области, лежит идея о том, что после применения декоррелирующего преобразования энергия, соответствующая информационной составляющей изображения, концентрируется в относительно небольшом числе низкочастотных спектральных компонент, в то время как энергия, соответствующая шуму, равномерно распределяется по всем спектральным компонентам. Таким образом, величина энергии, сосредоточенной в высокочастотных спектральных компонентах, определяется, главным образом, характеристиками шума, присутствующего на данном изображении [42].

Следовательно, обработав тем или иным образом высокочастотные спектральные коэффициенты, можно получить информацию о характеристиках (дисперсии) помех на данном изображении. В качестве декоррелирующих могут применяться различные ортогональные преобразования, например, ДКП [43 – 45] или вейвлет-преобразования (ВП) [46].

Среди достоинств методов, относящихся ко второй группе, следует отметить, как правило, неплохое быстродействие и относительную простоту реализации, и, главное, возможность обеспечения более точных оценок дисперсии помех для текстурных изображений и при малых значениях 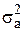. Недостатки же заключаются в следующем.

1. Методы, относящиеся к этой группе, работоспособны лишь при пространственно-некоррелированных помехах. Если шум является пространственно-коррелированным, его энергия распределяется по спектральным компонентам неравномерно и сосредотачивается, главным образом, в низкочастотной части спектра. Таким образом, нарушается основная идея, положенная в основу работы таких методов, и в результате анализа высокочастотных спектральных коэффициентов полученные оценки дисперсии оказываются, как правило, существенно заниженными по сравнению со своими истинными значениями (значения 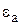могут достигать 0,7 [37]).

2. Применение данного подхода ограничивается только случаем, когда обрабатываемое изображение искажено аддитивным шумом. В принципе, при определенных условиях (использовании гомоморфных преобразований логарифмического вида и значениях 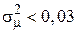) методы применимы и для оценивания дисперсии мультипликативных помех, однако на практике не всегда можно гарантировать, что 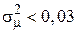, поэтому о достаточной универсальности этого подхода говорить не приходится.