Прямой, обратный, дополнительный коды
Мы будем изучать эти коды, т.к. в ЭВМ нет операции вычитания, и она заменяется операцией сложения с обратным кодом.
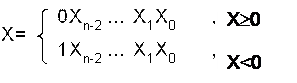
Прямым кодом целого двоичного числа Х будет называться число, образованное по формуле:
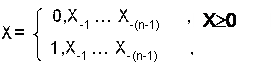
Прямым кодом дробного двоичного числа X будет число, образованное по формуле:
 | |||
 | |||
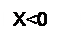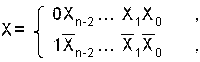Обратным кодом целого двоичного числа X называется число, образованное по формуле:
 |
 |
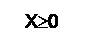Обратным кодом дробного двоичного числа X называется число, образованное по формуле:
 |
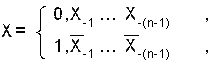
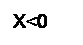Правило: Чтобы получить обратный код отрицательного двоичного числа, в знаковый разряд нужно поставить 1, а значащие разряды проинвертировать (0 заменить 1,а 1 заменить 0).
0 . 101
Знаковый разряд Значащие разряды
1 . 101
A = 0.0100 +4 прямой код;
А = 1.1011 -4 обратный код;
Для положительных чисел прямой и обратный коды совпадают.
Правило: Чтобы произвести суммирование(алгебраическое) двоичных кодов чисел с использованием обратных кодов необходимо все положительные числа представить в прямом коде, а отрицательные в обратном и просуммировать коды чисел, включая знаковые разряды.
Если возникает единица переноса из знакового разряда, то она прибавляется к младшему разряду.
Если в знаковом разряде получается 0, то это означает, что результат положительный и представлен в прямом коде.
Если в знаковом разряде результата 1, то это означает, что результат отрицательный и представлен в обратном коде.
Для получения прямого кода необходимо в знаковом разряде оставить 1, а значащие разряды проинвертировать (по правилу полинома можно переводить в десятичную систему счисления только прямой код числа).
Пример:
А=5, В=4
0.0101 +5 прямой код 0.0100 +4 прямой код
1.1010 -5 обратный код 1.1011 -4 обратный код
А+В
|
0.0100 +4 прямой код
 |
0.1001 +9 прямой код
А-В
|
 |
1.1011 -4 обратный код
1 0.0000
+1
0.0001 прямой код
Знаковый разряд результата равен 0. Из этого следует, что результат положительный и представлен в прямом коде.
В-А
|
1.1010 -5 обратный код
1.1110
Знаковый разряд результата равен 1. Следовательно, результат получился отрицательным и представлен в обратном коде. Прямой код результата равен:
1.0001 прямой код
Дополнительный код.
 |
Дополнительным кодом целого двоичного числа называется число, образованное по формуле:
 | |||
 | |||
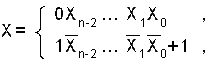Дополнительным кодом дробного двоичного числа называется число, образованное по формуле:
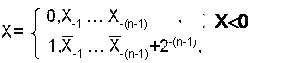
Правило: Чтобы получить дополнительный код двоичного отрицательного числа необходимо в знаковый разряд поставить 1, все значащие разряды проинвертировать и к младшему разряду прибавить 1.
Это применимо как для целых так и для дробных чисел.
Пример:
А=5, В=4
|
|
1 1
1.1011 -5 дополнительный код 1.1100 -4 дополнительный код
Для положительных чисел прямой и дополнительный коды совпадают.
Правило: Чтобы выполнить алгебраическое суммирование двоичных чисел с использованием дополнительного кода, положительные числа представляются в прямом коде, отрицательные – в дополнительном, и производится суммирование кодов чисел включая знаковые разряды.
При возникновении 1 переноса из знакового разряда – она отбрасывается.
Если в знаковом разряде 1, значит результат отрицательный и представлен в дополнительном коде.
Чтобы получить прямой код результата необходимо в знаковом разряде оставить 1, значащие разряды проинвертировать, к младшему разряду прибавить 1.
Пример:
А-В
|
0.0101 +5 прямой код
0.0001 +1 прямой код
Если образовался “0” в знаковом разряде, то число получилось положительным и представлено в прямом коде, а если “1”, то это число отрицательное и представлено в дополнительном коде.
Пример:
В-А
|
1.1011 -5 дополнительный код
1.1111
Знаковый разряд результата равен 1. Из этого следует, что результат получился отрицательным и представлен в дополнительном коде. Прямой код результата равен:
|
1.0001 -1 прямой код