Функциональные зависимости и нормальные формы
Ранее обсужденные правила категорной целостности и целостности на уровне ссылок накладывают ограничения на реляционную схему. Функциональные зависимости (ФЗ) позволяют накладывать дополнительные ограничения.
Функциональная зависимость–значение атрибута в кортеже однозначно определяет значение другого атрибута в кортеже. Формально функциональная зависимость определяется следующим образом: если А и В – атрибуты в таблице R, то запись
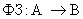
обозначает, что если два кортежа в таблице R имеют одно и то же значение атрибута А, то они имеют одно и то же значение атрибута В. Это определение также применимо, если А и В – множества столбцов, а не просто отдельные столбцы. Обозначение читается следующим образом: А функционально определяет В.
Атрибут в левой части ФЗ называется детерминантом. Детерминант–атрибут (атрибуты), значение которого определяет значения других атрибутов кортежей.
Реляционная таблица находится во второй нормальной форме (2НФ), если никакие неключевые атрибуты не являются функционально зависимыми лишь от части ключа. Таким образом, вторая нормальная форма может быть нарушена только в том случае, когда ключ составной.
Если таблица не удовлетворяет 2НФ, то возникают всевозможные аномалии (ввода, обновления, удаления). Для того, чтобы избавится от аномалий, таблицу необходимо разбить на две реляционные таблицы, каждая из которых удовлетворяет 2НФ. Эти две меньшие таблицы называются проекциями исходной таблицы. Проекция–таблица, состоящая из нескольких выбранных атрибутов другой таблицы. Процесс разбиения на две 2НФ-таблицы состоит из следующих шагов:
1) создается новая таблица, атрибутами которой будут атрибуты исходной таблицы, входящие в противоречащую правилу ФЗ. Детерминант ФЗ становится ключом новой таблицы;
2) атрибут, стоящий в правой части ФЗ, исключается из исходной таблицы;
3) если более одной ФЗ нарушают 2НФ, то шаги 1 и 2 повторяются для каждой такой ФЗ;
4) если один и тот же детерминант входит в несколько ФЗ, то все функционально зависящие от него атрибуты помещаются в качестве неключевых атрибутов в таблицу, ключом которой будет детерминант.
Реляционная таблица имеет третью нормальную форму (3НФ), если для любой функциональной зависимости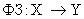 
, Х является ключом (то есть детеминант является ключом). Отсюда следует, что любая таблица, удовлетворяющая 3НФ, таже удовлетворяет и 2НФ. Если таблица не соответсвует 3НФ, то возникает избыточность данных, которая также приводит ко всевозможным аномалиям. Решение этих проблем – тоже разбиение.
Поскольку 3НФ-таблицы всегда удовлетворяют 2НФ, достаточно пользоваться критерием третьей нормальной формы. Если каждый детерминант в таблице является ключом этой таблицы, то таблицы удовлетворяет первой, второй и третьей нормальным формам. Это упрощает процесс нормализации, так как нужно проверить только один критерий.
Надо отметить, что данное определение третьей нормальной формы соответствует в некоторых источниках нормальной форме Бойса—Кодда.
В большинстве случаев достижение третьей нормальной формы а считается достаточным для реальных проектов баз данных, однако в теории нормализации существуют нормальные формы высших порядков, которые уже связаны не с функциональными зависимостями между атрибутами отношений, а отражают более тонкие вопросы семантики предметной области и связаны с другими видами зависимостей.
Первая нормальная форма запрещает иметь многозначные атрибуты. Однако существует много ситуаций, когда требуется многозначность.
Условие, обеспечивающее независимость атрибутов путем обязательного повтора значений, называется многозначной зависимостью (МЗЗ). МЗЗ является таким же ограничительным условием, как и ФЗ, так как они требуют огромного числа повторений значений данных. Важный этап нормализации состоит в избавлении от многозначных зависимостей. Таблица находится в четвертой нормальной форме, если она находится в третьей нормальной форме и не имеет многозначных зависимостей. Так как проблема многозначных зависимостей возникает в связи с многозначными атрибутами, то проблема многозначных зависимостей решается размещением каждого многозначного атрибута в свою собственную таблицу вместе с ключом, от которого атрибут зависит.
Рассмотрим конкретную ситуацию, понятную всем студентам. Пусть дано отношение, которое моделирует предстоящую сдачу экзаменов на сессии. Допустим, оно имеет вид:
(Номер зач.кн,. Группа, Дисциплина).
Перечень дисциплин, которые должен сдавать студент, однозначно определяется не его фамилией, а номером группы (то есть специальностью).
В данном отношении существуют следующие две многозначные зависимости:
Группа -» Дисциплина и Группа -» Номер зач.кн.
Это означает, что каждой группе однозначно соответствует перечень дисциплин по учебному плану и номер группы определяет список студентов, которые в этой группе учатся.
Если мы будем работать с исходным отношением, то мы не сможем хранить информацию о новой группе и ее учебном плане — перечне дисциплин, которые должна пройти группа до тех пор, пока в нее не будут зачислены студенты. При изменении перечня дисциплин по учебному плану, например, при добавлении новой дисциплины, внести эти изменения в отношение для всех студентов, занимающихся в данной группе, весьма затруднительно. С другой стороны, если мы добавляем студента в уже существующую группу, то мы должны добавить множество кортежей, соответствующих перечню дисциплин для данной группы. Эти аномалии модификации отношения как раз и связаны с наличием двух многозначных зависимостей.
В этом примере можно произвести декомпозицию исходного отношения в два отношения:
(Номер зач.кн.. Группа),
(Группа, Дисциплина).
Оба эти отношения находятся в четвертой нормальной форме и свободны от отмеченных аномалий. Действительно, обе операции модификации теперь упрощаются: добавление нового студента связано с добавлением всего одного кортежа в первое отношение, а добавление новой дисциплины выливается в добавление одного кортежа во второе отношение. Кроме того, во втором отношении мы можем хранить любое количество групп с определенным перечнем дисциплин, в которые пока еще не зачислены студенты.
Последней нормальной формой является пятая нормальная форма 5NF, которая
редко используется на практике. В большей степени она является теоретическим исследованием.