Методические указания. Для перевода восьмеричного или шестнадцатеричного числа в двоичную формудостаточно
Для перевода восьмеричного или шестнадцатеричного числа в двоичную формудостаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (см. таблицу 1) или четырехразрядным двоичным числом (тетрадой) (см. таблицу 1), при этом отбрасывают незначащие нули в старших и младших (после запятой) разрядах.
Примеры. а) 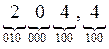 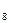 = = 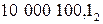 ; б) ; б) 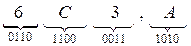 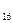 = = 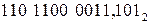 . . |
Задание 6.Переведите числа из восьмеричной и шестнадцатеричной систем счисления в двоичную систему.
Методические указания.
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Примеры.
а) Перевести 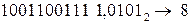 с.с.
с.с.
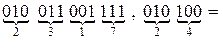

б) Перевести 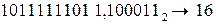 с.с.
с.с.
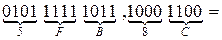
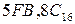
Задание 7.Переведите числа из восьмеричной в шестнадцатеричную систему счисления и из шестнадцатеричной в восьмеричную систему счисления.
Методические указания.
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Пример. Перевести 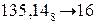 с.с.
с.с.
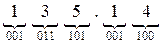
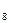
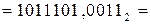
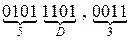
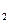
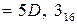
Ответ: 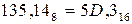 .
.
Задания для самостоятельной работы
| Вари-ант | Переведите числа в 10-ю с.с. | Переведите десятичные числа в 2-ю, 8-ю и 16-ю с.с. | Восьмеричное число переведите в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с. |
| 1. | 10010011111, 1012 1372,128 3CA,7D16 | 286,06 | 1263,718 2BA,2C16 |
| 2. | 11100101010, 0112 2136,318 1C3,A216 | 476,91 | 3472,628 4CA,2716 |
| 3. | 11001100111, 0112 1742,368 123E,4D16 | 438,76 | 1724,318 2АF,3C16 |
| 4. | 11101011101, 10012 1467,638 1AF,7316 | 362,87 | 1273,568 30A,E0F16 |
| 5. | 101011010110, 0012 1523,248 2А7,3Е16 | 305,37 | 1623,728 5C2,C716 |
| 6. | 11001100011, 10012 1273,568 30A,E0F16 | 324,93 | 12372,418 1D2,7D1 |
| 7. | 10011010111, 0112 1623,728 5C2,C716 | 457,21 | 1735,128 5AD,4D16 |
| 8. | 11000001111, 0112 1735,668 23A,EF16 | 343,43 | 2451,238 2BA,D316 |
| 9. | 10000111111, 10012 1327,468 3CD,BA16 | 381,93 | 1372,128 3CA,7D16 |
| 10. | 11100001101, 0112 1523,748 4BA,2F16 | 419,96 | 2136,318 1C3,A216 |
| 11. | 11011110110, 1012 4123,178 1C3,A516 | 400,01 | 1742,368 123E,4D16 |
| 12. | 110010010111, 10012 1272,128 3AD,7D16 | 153,63 | 5123,148 1B3,4D16 |
| 13. | 11100110101,10112 1071,218 5DC,F216 | 172,04 | 1263,718 2BA,2C16 |
| 14. | 10011010111, 0112 2372,128 1F2,7B16 | 191,11 | 3472,628 4CA,2716 |
| 15. | 11110010101,10012 1574,618 35C,F116 | 210,96 | 1724,318 2АF,3C16 |
| 16. | 11000011010, 10012 6123,518 13A,C216 | 229,74 | 1272,128 3AD,7D16 |
| 17. | 10011000111,11112 5412,638 52A,1716 | 248,2 | 1071,218 5DC,F216 |
| 18. | 11101101101, 10012 5123,148 1B3,4D16 | 267,72 | 2372,128 1F2,7B16 |
| 19. | 11101011001, 01012 1263,718 2BA,2C16 | 571,58 | 1742,368 123E,4D16 |
| 20. | 10101110111, 01012 3472,628 4CA,2716 | 590,72 | 1467,638 1AF,7316 |
| 21. | 10101101111, 0112 1724,318 2АF,3C16 | 495,32 | 1523,248 2А7,3Е16 |
| 22. | 11100101101,10112 1275,468 23А,Е716 | 552,5 | 1735,668 23A,EF16 |
| 23. | 10011010111, 0112 12372,418 1D2,7D1 | 533,51 | 1327,468 3CD,BA16 |
| 24. | 11011100010,11012 1735,128 5AD,4D16 | 514,58 | 1523,748 4BA,2F16 |
| 25. | 10100101111, 1012 2451,238 2BA,D316 | 609,11 | 4123,178 1C3,A516 |
Контрольные вопросы.
1. Как осуществляется перевод чисел из р-ой с.с. в десятичную
2. Как перевести целое десятичное число в р- ую с.с.
3. Как перевести правильную десятичную дробь в р- ую с.с.
4. Как перевести неправильную десятичную дробь в р- ую с.с.
* Здесь и в дальнейшем при одновременном использовании нескольких различных систем счисления основание системы к которой относится число будем указывать в виде нижнего индекса.
