ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Способы контроля правильности передачи данных
Способы контроля правильности передачи данных. Код с проверкой на четность.Контроль целостности информации при передаче от источника к приемнику может осуществляться с использование кодирующих кодов.
Простейший кодирующий код – код с проверкой на честность, который образуется добавлением к группе информационных разрядов одного избыточного, значения которое выбирается таким образом, чтобы сумма единиц в кодовой комбинации, т.е. вес кодовой комбинации, была всегда четна.
Пример 1. Рассмотрим код с проверкой на четность, образованный добавлением контрольного заряда к простому двоичному коду:
| Информационные разряды | Контрольные разряды | |
Такой код обнаруживает все одиночные ошибки и групповые ошибки нечетной кратности, так как четность количества единиц в этом случае будет также нарушаться.
Следует отметить, что при кодировании целесообразно число единиц в кодовой комбинации делать нечетным и осуществлять контроль на нечетность. В этом случае любая комбинация, в том числе и изображающая ноль, будет иметь хотя бы одну единицу, что дает возможность отличить полное отсутствие информации от передачи нуля.
Коды Хэмминга. N – значный код Хэмминга имеет m – информационных разрядов и k – контрольных. Число контрольных разрядов должно удовлетворять соотношению
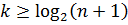 ,
,
откуда 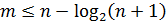 .
.
Код Хэмминга строится следующим образом; к имеющимся информационным разрядам кодовой комбинации добавляется вычисленное по вышеприведённой формуле количество контрольных разрядов, которые формируются путем подсчета четности суммы единиц для определенных групп разрядов. При приёме такой кодовой комбинации из полученных информационных и контрольных разрядов путем аналогичных подсчётов четности составляют корректирующие число, которое равно нулю, при отсутствии ошибки, либо указывает номер ошибочного разряда.
Рассмотрим подробнее процесс кодирования. Пусть первый контрольный разряд имеет нечетный порядковый номер, установим его при кодировании таким образом, чтобы сумма единиц всех разрядов с нечетными порядковыми номерами была равна нулю. Такая операция может быть записана в виде следующего соотношения:
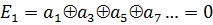 ,
,
где 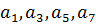 – двоичные символы, размещенные в разрядах с номерами 1,3,5,7,…
– двоичные символы, размещенные в разрядах с номерами 1,3,5,7,…
Появление единицы во втором разряде (справа) корректирующего числа означает ошибку в тех разрядах кодовой комбинации, порядковые номера которых (2, 3, 6, 7, …)в двоичном изображении имеют единицу во втором справа разряде. Поэтому вторая операция кодирования, позволяющая найти второй контрольный разряд, имеет вид
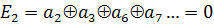 .
.
Рассуждая аналогичным образом:
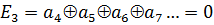 ,
,
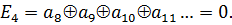
После приема кодовой комбинации совместно со сформированными контрольными разрядами выполняются те же операции подсчёта, что были описаны выше, а полученное число
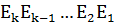
cчитается корректирующим, причем при 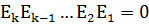 ошибки отсутствуют, а при наличии ошибок неравным нулю оказываются те суммы
ошибки отсутствуют, а при наличии ошибок неравным нулю оказываются те суммы 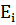 , в образовании которых участвовал ошибочный разряд. Корректирующее число при этом будет равно порядковому номеру этого разряда.
, в образовании которых участвовал ошибочный разряд. Корректирующее число при этом будет равно порядковому номеру этого разряда.
Выбор места для контрольных разрядов в каждой из кодовых комбинаций определяется таким образом, чтобы контрольные разряды участвовали только в одной операции подсчёта четности. Такими позициями являются целые степени двойки: 1, 2, 4, 8, 16, …
Пример 2. Составим шестизначный код Хэмминга (табл. 1) для 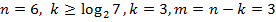
Таблица 1
| Цифра | Простой двоичный код | Код Хэмминга 6 5 4 3 2 1 |
Варианты исправления ошибок:
Принят код: 111100 исправлено 110100 - ошибка по корректирующему числу в разряде 4;
Принят код: 111010 исправлено 101010 - ошибка по корректирующему числу в разряде 5;
Принят код: 100000 исправлено 000000 - ошибка по корректирующему числу в разряде 6.
Циклические коды. Циклические коды – разновидность систематических кодов и поэтому обладают всеми их свойствами. Характерной особенностью циклического кода, определяющей его название, является то что если
n-значная кодовая комбинация 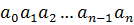 принадлежит данному коду, то и комбинация
принадлежит данному коду, то и комбинация 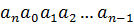 , полученная циклической перестановки знаков, также принадлежит этому коду.
, полученная циклической перестановки знаков, также принадлежит этому коду.
Идея построения циклических кодов базируется на использовании неприводимых многочленов. Неприводимым называется многочлен, который не может быть представлен в виде произведения многочленов низших степеней, т.е. такой многочлен, который делится только на самого себя или на единицу.
Неприводимые многочлены при построении циклических кодов играют роль так называемых образующих полиномов, от вида которых, собственно, и зависят основные характеристики полученного кода: избыточность и корректирующая способность. В табл. 2 указаны неприводимые многочлены со степенями 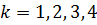 .
.
Таблица 2
| K | P(x) | P(1,0) |
| k=1 | 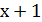 | |
| k=2 | 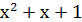 | |
| k=3 | 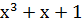 | |
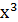 + + 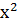 +1 +1 | ||
| k=4 | 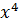 + + 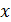 +1 +1 | |
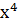 + + 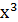 +1 +1 | ||
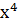 + + 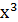 + + 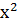 +x+1 +x+1 |
Основные принципы кодирования в циклическом коде заключается в следующем. Двоично-кодированное n-разрядное число представляется полиномом (n-1)-й степени некоторой переменной х, причем коэффициентами полинома являются двоичные знаки соответствующих разрядов. Запись, чтение и передача кодовых комбинаций в циклическом коде производится, начиная со старшего разряда. В соответствии с этим правилом в дальнейшем сами числа и соответствующие им полиному будем записывать так, чтобы старший разряд оказывался справа:
Пример 3. Число 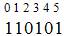 (нумерация разрядов согласно выше приведенному правилу, ведется слева на право от 0 до 5) будет представлено полиномом пятой степени: 1+x+
(нумерация разрядов согласно выше приведенному правилу, ведется слева на право от 0 до 5) будет представлено полиномом пятой степени: 1+x+  +
+ 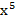 .
.
Следует отметить, что циклическая перестановка разрядов в двоичном представлении числа соответствует умножению полинома на х, при котором 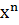 заменяется единицей и переходит в начало полинома.
заменяется единицей и переходит в начало полинома.
Пример 4. Выполним умножение полинома, полученного в предыдущем примере, на х. Новый полином x+ 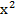 +
+ 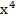 +
+ 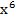 преобразуем, заменив
преобразуем, заменив 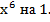
Окончательно получим 1+ x + 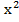 +
+ 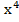 , что соответствует числу 111010.
, что соответствует числу 111010.
Циклический код n-значного числа, как и всякий систематический код состоит из m информационных и k контрольных знаков, причём последние занимают k младших разрядов. Поскольку последовательная передача кодовых комбинаций производится, как уже указывалось, начиная со старших разрядов, контрольные знаки передаются в конце кода.
Образование кода выполняется при помощи так называемого порождающего полинома, P(х) степени k, видом которого определяется основные свойства кода – избыточность и корректирующая способность.
Кодовым полином F(x) является полином степени, меньшей (m+k), если он делится без остатка на порождающий полином P(x). После передачи сообщения декодирование состоит в выполнении деления полинома H(х), соответствует принятому коду, на Р(х). При отсутствии ошибок Н(х)=F(x), и деление выполняется без остатка. Наличие ненулевого остатка указывает на то, что при передаче или хранении произошли искажения информации.
Для получения систематического циклического кода используется следующее соотношение:
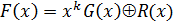 ,
,
где G(x) – полином, представляющий информационные символы (информационный полином); R(x)- остаток от деления 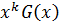 на Р(х).
на Р(х).
Пример 5. Рассмотрим кодирование восьмизначного числа 10110111. Пусть для кодирования задан порождающий полином третей степени 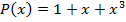
Делим 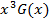 на
на 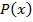 , где
, где 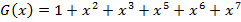 :
:
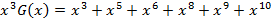
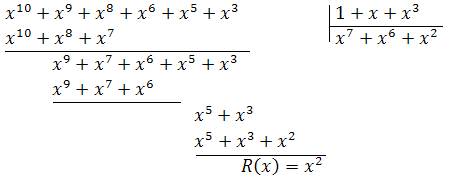
Используя соотношение для получения систематического циклического кода, находим 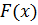 :
:
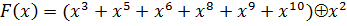
Таким образом, окончательно кодовая комбинация, соответствующая 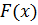 , имеет вид
, имеет вид
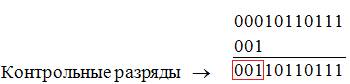
Практически применяемая процедура кодирования ещё более проста. Так как нас интересует только остаток, а частное в конечном результате не используется, то можно производить последовательное вычитание по mod 2 делится из делимого и полученных разностей до тех пор, пока разность не будет иметь более низкую степень, чем делитель. Это разность и есть остаток. Такой алгоритм может быть реализован аппаратно при помощи
k- разрядного сдвигающего регистра, имеющего обратные связи. Очевидно, что полученный этим способом циклический код будет являться систематическим.
Существует и второй способ получения циклического кода, когда очередная кодовая комбинация образуется путем умножения кодовой комбинации 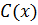 простого n-значного кода на образующий полином
простого n-значного кода на образующий полином 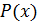 . При этом способе образования циклических кодов информационные и контрольные символы в комбинациях циклического кода не отделены друг от друга, что затрудняет процесс декодирования. Поэтому такой способ кодирования применяется реже, чем первый.
. При этом способе образования циклических кодов информационные и контрольные символы в комбинациях циклического кода не отделены друг от друга, что затрудняет процесс декодирования. Поэтому такой способ кодирования применяется реже, чем первый.
Пример 6. Рассмотрим кодирование вторым способом, причём при выполнении операции будем использовать непосредственно записи исходных кодовых комбинаций в двоичном виде. Дан порождающий полиномом вида 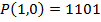 . Требуется построить циклический код из простого четырёхзначного кода вторым способом. Для построения в качестве примера используем исходную комбинацию
. Требуется построить циклический код из простого четырёхзначного кода вторым способом. Для построения в качестве примера используем исходную комбинацию 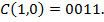 Операция умножения этой комбинации на образующий полином запишиться следующим образом:
Операция умножения этой комбинации на образующий полином запишиться следующим образом:

Аналогичным образом получены остальные кодовые комбинации несистематического циклического кода, приведенные в табл. 3.
Таблица 3
Простой четырёх символьный код 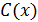 | Циклический (7,4)- код 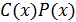 ,где ,где 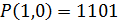 |
Проблема обнаружения различного типа ошибок с помощью циклического кода, как уже указывалось, сводится к нахождению нужного порождающего полинома (данный вопрос не входит в рассмотрение, полно основные принципы подбора порождающих полиномов вы можете изучить самостоятельно).
Эффективное кодирование информации. Общие положения. Напомним что кодирование – представление сообщений в форме, удобной для передачи по данному каналу, а декодирование – восстановление информации по принятому сигналу. Одним из важнейших вопросов кодирования является повышения его эффективности, т.е. путем устранения избыточности снижения среднего числа символов, требующихся на букву сообщения. Такое кодирование получило название эффективное кодирование. Из сказанного выше следует, что эффективное кодирование решает задачу максимального сжатия информации.
Учитывая статические свойства источника информации, можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии помех позволяет уменьшить время передачи сообщения и его объем.
Эффективное кодирование базируется на основной теореме Шеннона для канала без помех, суть которой сводиться к следующему: сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.
Наличие в сообщениях избыточности позволяет рассматривать вопрос о сжатии данных, т.е. о передачи того же количества информации с помощью последовательностей символов меньшей длинны – методы сжатия без потерь (обратимые). Для этого используют специальные алгоритмы сжатия, уменьшающие избыточность. Эффект сжатия оценивают коэффициентом сжатия
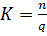 ,
,
где n – число минимально необходимых символов для передачи сообщения;
q – число символов в сообщении, сжатом данным методом.
Так при эффективном двоичном кодировании n равно энтропии источника информации.
Наряду с методами сжатия, не уменьшающими количество информации в сообщении, применяют методы сжатия, основанные на потере малосущественной информации, – методы сжатия с потерями (необратимые). Следует отметить, что применение методов сжатия с потерями не приемлемо для некоторых видов информации, например текстовой или числовой.
Обратимое сжатие всегда приводит к снижению объема выходного потока информативности. Из выходного потока при помощи восстанавливающего алгоритма можно получить исходный поток.
Основные методы обратимого сжатия:
- Шеннона – Фано (Shannon – Fano);
- Хаффмена (Huffman);
- LZW (Lanper – Ziv – Welch);
- арифметическое сжатие.
Преобразование входного потока данных, при котором входной поток представляет похожий по внешним характеристикам на выходной поток объект, однако отличается от него объемом. Используется понятие качества – степени соответствия исходного и результатирующего потока.
Основные алгоритмы необратимого сжатия:
- MPEG (Moving Pictures Experts Group);
- JPEG (Joint Photographic Experts Group);
- фрактальное сжатие.
Простейший способ сжатия числовой информации, представленной в коде ASCII, заключается в использовании сокращенного кода четырьмя битами на символ вместо 8, так как в ASCII-кодировке цифры, а так же символы «.», «,» и « » в качестве первого кодового символа имеют нуль, который может быть отброшен.
Среди широко используемых благодаря своей простоте алгоритмов сжатия наиболее известен алгоритм RLE (Run Length Encoding), в котором вместо передачи цепочки из одинаковых символов передаются символ и значение длинны цепочки. Этот метод эффективен при передаче растровых изображений, особенно монохромных, где имеется большое число цепочек из единиц и нулей, но малополезен при передачи текста. Алгоритм RLE реализован в формате PCX.
Пример 7. Рассмотрим сжатие по алгоритму RLE.
Исходный текст (9 байт): 77 77 77 77 11 11 11 01 FF
В исходной последовательности:
1) выделяется повторяющаяся последовательность байт;
2) заменяется счётчиком повторов (04) и кодирующим байтом(77);
3) 00-нет повторений;
4) 02-сколько байт не повторяется;
5) какие байты не повторяются(01 FF).
Результат сжатия (8 байт): 04 77 03 11 00 02 01 FF.
Недостатками алгоритма RLE являются:
- низкая степень сжатия;
- сильная зависимость от количества повторов байт в исходной информационной последовательности.
Достоинство этого алгоритма состоит в простоте его реализации.
Основная сфера использования методов сжатия с потерями – графические, аудео и видео файлы, где есть возможность, частично пожертвовав качественными характеристиками информации, добиться значительного уменьшения его объемов.
Наибольшее распространение среди методов сжатия информации без потерь нашли статические алгоритмы сжатия, учитывающие вероятность появление отдельных символов в информационном потоке. В первую очередь это алгоритмы Шеннона – Фано и Хаффмена.
Алгоритм Шеннона – Фано. Эффективное кодирование методом Шеннона – Фано базируется на основной теореме Шеннона для канала без помех.
Алгоритм Шеннона – Фано:
§ буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей;
§ буквы алфавита разделяются на две группы так, чтобы суммы вероятностей в каждой группе были по возможности одинаковы;
§ всем буквам верхней половины в качестве первого символа приписывается единица, а всем нижним нули;
§ каждая из полученных групп в свою очередь разбивается на две подгруппы с одинаковыми суммарными вероятностями и т.д., процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.
Пример 8. Рассмотрим алфавит из семи букв, приписав каждой букве вероятность ее появления в сообщении 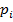 (существуют специальные таблицы вероятностей появления букв русского или латинского алфавитов в сообщениях, например, таблица 4).
(существуют специальные таблицы вероятностей появления букв русского или латинского алфавитов в сообщениях, например, таблица 4).
Таблица 4
| Буква | Вероятность 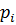 | Процесс получения кода | Код Шеннона | |||
| A | 1/4 | |||||
| E | 1/4 | |||||
| F | 1/8 | |||||
| C | 1/8 | |||||
| B | 1/8 | |||||
| D | 1/16 | |||||
| G | 1/16 |
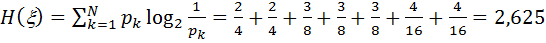 .
.
При обычном двоичном кодировании, не учитывая статических характеристик, для предоставления каждой буквы потребуется три символа. Наибольший эффект сжатия получается в случае, когда вероятности букв представляют собой целочисленные отрицательные степени двойки. Среднее число символов на букву в этом случае точно равно энтропии.
Среднее число символов на букву:
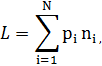
где 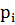 – вероятность появления i-го символа алфавита;
– вероятность появления i-го символа алфавита; 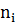 – количество символов в кодовой комбинации i-го символа алфавита.
– количество символов в кодовой комбинации i-го символа алфавита.
Для рассмотренного примера 8
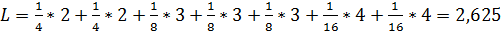 .
.
Разность величин (L – H) – избыточность кода, а величина (L – H)/L – относительная избыточность.
Избыточность может тактироваться как мера бесполезно совершаемых альтернативных выборов. Поскольку в практических случаях отдельные знаки никогда не встречаются одинаково часто, то кодирование с постоянной длинной кодовых слов в большинстве случаев избыточно. Не смотря на это руководствуясь техническими соображениями, такое кодирование применяется достаточно часто.
Алгоритм Хаффмена. Суть алгоритма Хаффмена сводится к следующему:
§ буквы алфавита сообщений выписываются в основной столбец таблицы в порядке убывания вероятностей;
§ две последние буквы объединяются в одну вспомогательную букву, которой приписывается суммарная вероятность;
§ вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагается в порядке убывания вероятностей, а две последние объединяются до тех пор, пока не получат единственную вспомогательную букву с вероятностью единица;
§ далее для построения кода используется бинарное дерево, в корне которого располагается буква с вероятностью единица, при ветвлении ветви с большей вероятностью присваивается код единица, а с меньшей код ноль).
Пример 9. Рассмотрим условный алфавит из восьми букв, каждой из которых приписана соответствующая вероятность ее появления в сообщении (табл. 5).
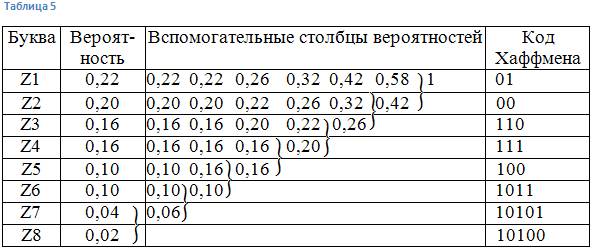
L = 0,22 * 2 + 0,20 * 2 + 0,16 * 3 + 0,16* 3 + 0,10 * 3 + 0,10 * 4 + 0,04 * 5 +0,02*5 = 2,8;
Н = 2,76;
L — Н = 0,04.
Для сравнения: в коде Шеннона с таким же распределением вероятностей L - Н = 0,08. Бинарное дерево изображено на рис. 1.
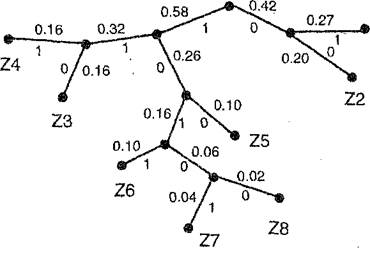
Рис. 1.Бинарное дерево
Для построения кодов Шеннона — Фано и Хаффмена можно использовать таблицу вероятности отдельных букв в русском языке (табл. 6).
Таблица 6
| Буква | Вероятность | Буква | Вероятность |
| пробел | 0,175 | Я | 0,018 |
| О | 0,090 | Ы | 0,016 |
| Е | 0,072 | 0,016 | |
| А | 0,062 | Ъ,Ь | 0,014 |
| И | 0,062 | Б | 0,014 |
| Т | 0,053 | Г | 0,013 |
| Н | 0,053 | Ч | 0,012 |
| С | 0,045 | Й | 0,010 |
| Р | 0,040 | X | 0,009 |
| В | 0,038 | Ж | 0,007 |
| Л | 0,035 | Ю | 0,006 |
| К | 0,028 | Ш | 0,006 |
| М | 0,026 | Ц | 0,004 |
| Д | 0,025 | Щ | 0,003 |
| П | 0,023 | Э | 0,003 |
| У | 0,021 | Ф | 0,002 |
