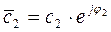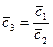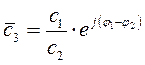Взаимные преобразования реального источника э.д.с. в реальный источник тока и наоборот
Сравнивая вольт-амперные характеристики реального источника тока и реального источника э.д.с. можно сделать вывод, что они подобны. Следовательно, можно осуществить преобразование и перейти от реального источника тока к реальному источнику э.д.с. и наоборот.
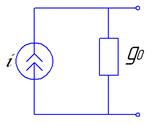 Источник тока реальный, Источник тока реальный, 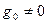 | Источник э.д.с. реальный, 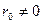 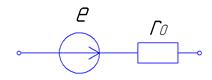 |
Известны 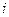 , , 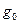  | 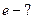 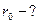  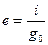 ; ; 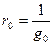 |
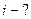 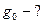 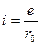 ; ; 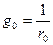 | Известны 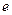 , , 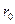 |
Если 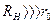 , то это идеальный источник э.д.с. (
, то это идеальный источник э.д.с. ( 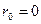 ).
).
Если 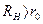 , то это реальный источник э.д.с. (
, то это реальный источник э.д.с. ( 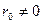 ).
).
Если 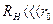 (
( 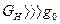 , так как
, так как 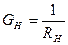 ,
, 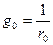 ), то это идеальный источник тока (
), то это идеальный источник тока ( 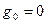 ).
).
Если 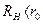 (
( 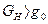 ), то это реальный источник тока (
), то это реальный источник тока ( 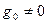 ).
).
Тема 3. Переменный ток
Переменный ток и его параметры
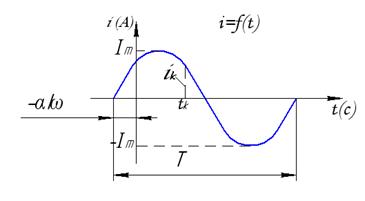 Переменным или синусоидальным током будем называть ток, изменяющийся по закону
Переменным или синусоидальным током будем называть ток, изменяющийся по закону  .
.
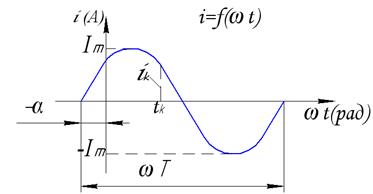 |
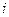 - мгновенное значение переменного тока (А), в момент времени
- мгновенное значение переменного тока (А), в момент времени 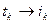 ;
;
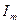 - амплитудное значение переменного тока (А);
- амплитудное значение переменного тока (А);
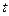 - время (с);
- время (с);
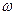 - угловая частота переменного тока (
- угловая частота переменного тока ( 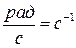 ),
), 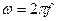 ;
;
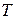 - период переменного тока (с);
- период переменного тока (с);
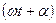 - фаза переменного тока (рад);
- фаза переменного тока (рад);
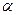 - начальная фаза переменного тока, т.е. фаза при
- начальная фаза переменного тока, т.е. фаза при 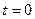 (рад).
(рад).
Изображение синусоидальных процессов с помощью вращающихся векторов
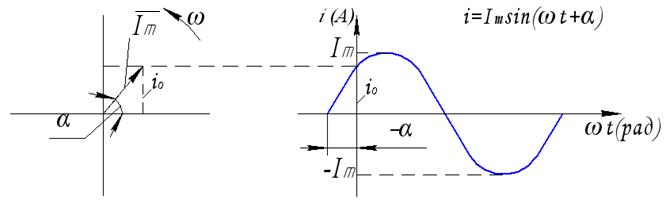 |
 - мгновенное значение тока при
- мгновенное значение тока при  ,
, 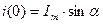 .
.
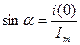
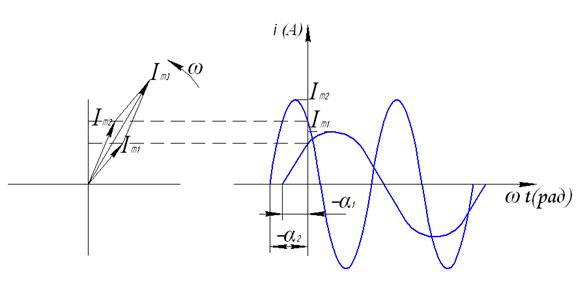
Если вращать вектор 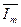 со скоростью
со скоростью 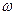 против часовой стрелки, то он своим концом опишет состояние мгновенного значения тока в любой момент времени. Таким образом синусоидальный ток, представленный в виде
против часовой стрелки, то он своим концом опишет состояние мгновенного значения тока в любой момент времени. Таким образом синусоидальный ток, представленный в виде  , можно представить графически в виде вектора, равного по размеру
, можно представить графически в виде вектора, равного по размеру 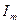 , с начальной фазой
, с начальной фазой 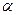 и вращающегося со скоростью
и вращающегося со скоростью 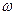 против часовой стрелки.
против часовой стрелки.
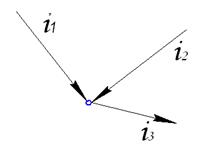
Пусть 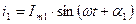 ,
, 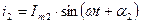 ,
, 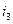 - ?
- ?
По 1 закону Кирхгофа 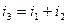 .
.
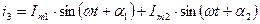
Достоинством векторного представления синусоидальных величин является то, что действия над синусоидальными величинами (сложение, вычитание и др.) значительно упрощаются благодаря применению правил векторного суммирования и перемножения.
Векторное представление переменного тока удобно осуществлять на комплексной плоскости и использовать правила действия над комплексными числами.
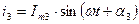
Комплексные числа
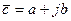 - алгебраическая форма комплексного числа, где
- алгебраическая форма комплексного числа, где 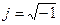 ,
,
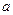 -вещественная часть,
-вещественная часть,
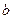 - мнимая часть.
- мнимая часть.
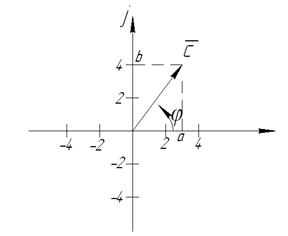
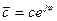 - показательная форма комплексного числа, где
- показательная форма комплексного числа, где 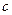 - модуль комплексного числа,
- модуль комплексного числа,
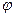 - аргумент.
- аргумент.
Пусть 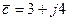
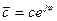
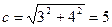
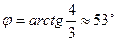
Преобразование алгебраической формы комплексного числа в показательную
И наоборот
Алгебраическая форма 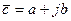 | Показательная форма 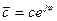 | |||
Известны 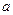 , , 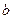
| 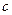 -? -? 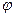 -? -? 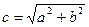 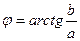 | |||
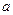 -? -? 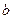 -? -? 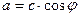 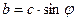 |  Известны Известны 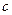 , , 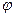 |
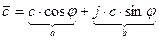 - тригонометрическая форма комплексного числа
- тригонометрическая форма комплексного числа
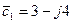

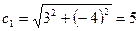
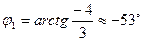
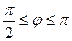
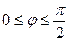
Следовательно 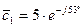
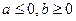
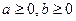

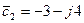
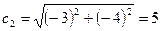
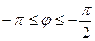
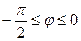
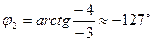
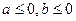
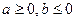
Следовательно 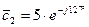
Действия над комплексными числами
1. Суммирование
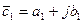 ,
, 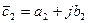
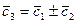
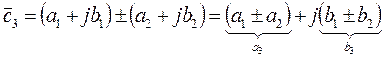
2. Умножение
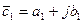 ,
, 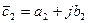
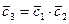
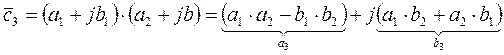
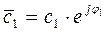 ,
, 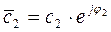
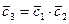
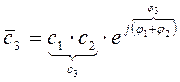
3. Деление
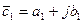 ,
, 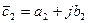
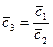
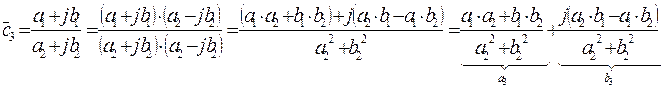
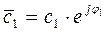 ,
,