Структурная схема цифровой следящей системы

Структура дискретной системы автоматического управления

Использование цифровых методов обработки информации в системах автоматического управления позволяет реализовывать сложные алгоритмы управления и обеспечивать их быструю сменяемость. Кроме того, цифровые устройства, как правило, более надежны в работе и имеют меньшие габариты и массу. Автоматические системы, полностью построенные на цифровых элементах, называются цифровыми САУ (ЦСАУ). Особенно широкое распространение ЦСАУ получили в радиотехнических системах для обработки информации о параметрах радиосигналов. Например, в радиолокационных системах эти параметры (амплитуда, частота, фаза и др.) несут информацию о координатах объектов, поэтому в них используют ЦСАУ для слежения за угловыми координатами, дальностью и скоростью перемещения целей. В радиотехнических следящих системах входная информация передается с помощью радиосигналов, а выходная, как правило, в виде электрических сигналов, что дает возможность выполнить систему только из электронных элементов и устройств. В том случае, когда выходная информация должна выдаваться в виде линейных или угловых перемещений, используют электрические и электромеханические цифровые элементы. Сигналы в ЦСАУ формируются в виде последовательности импульсов, образующих некоторый код, с помощью которого записываются мгновенные значения процессов, подлежащих обработке.

Кодовая модуляция сигналов приводит к тому, что информация в системе квантуется как по времени, так и по уровню. Квантование по времени происходит из-за импульсного "характера сигналов, в результате чего полезная информация выдается в виде дискретной функции x(iT_n). Квантование по уровню происходит за счет конечного числа импульсов в коде, называемого числом разрядов. При конечном числе разрядов можно отобразить лишь конечное число дискретных значений передаваемого процесса. Например, в случае двоичного кода при числе разрядов q максимальное число дискретных значений процесса

N = 2^q - 1.

Так, если код имеет 8 разрядов, то N = 225; если q = 12, то N = 4095. При заданном числе разрядов передаваемый процесс x(iT_n) может отображаться не более чем N дискретными значениями.

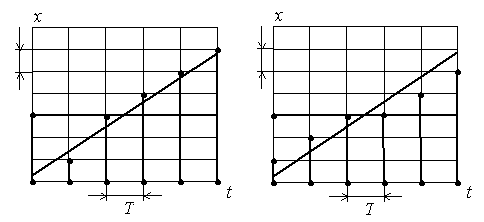
Рис. 1.19. Два способа квантования по уровню

Если максимальное значение процесса равно x_mах, а минимальное x_min, то шаг квантования по уровню

Δ =

xmах - xmin N

.

В результате квантования по уровню получается процесс 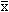(iT_n), который будет лишь приближенно отражать характер изменения процесса x(iT_n). Ошибка приближения (округления) будет зависеть от шага квантования и способа квантования по уровню, два из которых показаны на рис. 1.19. В первом случае квантование по уровню происходит по правилу: принимается значение 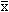(iT_n), ближайшее к x(iT_n) (рис. 1.19, а). Во втором принимается значение 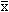(iT_n), ближайшее к x(iT_n) снизу для x(iT_n) > 0 и сверху для x(iT_n) < 0 (рис. 1.19,б). Квантование по уровню является безынерционным нелинейным преобразованием типа многоступенчатой релейной характеристики, показанной на рис. 1.19, и обозначается в виде функции

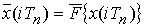
Статическая характеристика квантователя для первого способа квантования показана на рис. 1.20, а, а для второго - на рис. 1.20, б. Прямые, проходящие через начало координат, соответствуют случаю линейного преобразования. Из характеристик на рис. 1.20 видно, что ошибка округления при первом способе квантования равна 0.5Δ, а при втором - Δ. Хотя первый способ квантования обладает более высокой точностью, однако его техническая реализация сложнее второго. Ошибка округления является инструментальной погрешностью ЦСАУ, определяющей точность работы в статике, и большей точности в цифровых системах достигнуть невозможно. Величину ошибок округления можно уменьшить путем увеличения числа разрядов кода, однако это приводит к усложнению конструкции цифровых элементов. В динамических условиях работы ошибки могут быть значительно выше ошибок округления и играют определяющую роль, поэтому методике их расчета в дальнейшем уделяется особое внимание. Наличие квантования по уровню может приводить к появлению автоколебаний, амплитуда и частота которых зависят от шага квантования Δ.

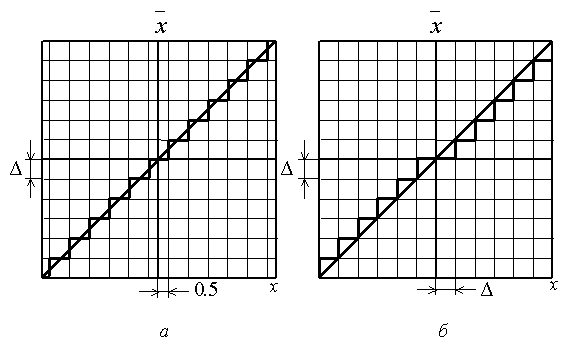
Рис. 1.20. Статические характеристики квантователей

Таким образом, цифровая обработка информации имеет ряд специфических особенностей, которые надо учитывать в процессе исследования ЦСАУ.

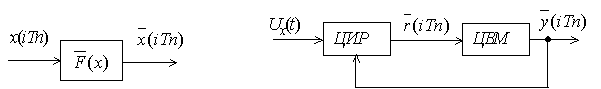
Рис. 1.21. Структурная схема квантователя

Рис. 1.22. Функциональная схема ЦСАУ

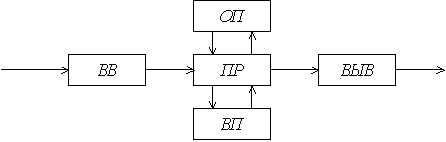
Рис. 1. 23. Функциональная схема ЦВМ

Цифровое представление информации в ЦСАУ можно отобразить с помощью двух последовательно выполняемых операций: квантования по времени и квантования по уровню. Квантование по времени является операцией линейной, а по уровню - нелинейной, в результате чего ЦСАУ относятся к классу нелинейных систем. На структурных схемах операцию квантования по уровню отображают нелинейным звеном с характеристикой (рис. 1.21). Наиболее широкое распространение получили электронные цифровые следящие системы на базе цифровых вычислительных машин (ЦВМ), функциональная схема которых изображена на рис. 1.22. В цифровом измерителе рассогласования (ЦИР) формируется в цифровой форме рассогласование

,

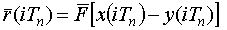которое поступает и обрабатывается на ЦВМ. На рисунке 1.23 изображена упрощенная функциональная схема машины, где ВВ и ВЫВ - устройства ввода и вывода; ПР - процессор; ОП - оперативная память; ВП - внешняя память. ПР предназначен для проведения операций над числами, ОП - для хранения промежуточных результатов и команд, ВП - для хранения алгоритмов обработки информации и исходных данных. Главной особенностью ЦВМ является работа в реальном масштабе времени. Это значит, что вся обработка поступающей информации должна заканчиваться за время Т_П (период квантования процессов по времени), и это накладывает жесткие требования на быстродействие машины, а оно, в свою очередь, часто определяет минимальное значение Т_n. Так как частота квантования

Ω =

2 π Tn

должна удовлетворять теореме Котельникова (п.1.2), то быстродействие ЦВМ может существенно влиять на качество работы системы. Время обработки информации машиной Т₀ складывается из времени ввода и вывода данных, времени обращения к памяти и времени проведения операций в процессоре. При работе в реальном масштабе времени

T₀ = α T_n,

где коэффициент 0 < α ≤ 1. Таким образом, выдача данных из ЦВМ будет происходить с запаздыванием на время αT_n относительно момента их поступления, поэтому машина в составе ЦСАУ может рассматриваться как запаздывающее звено с передаточной функцией

K_цвм(p) = e^{-p α Tn}.

Так как в теории z-преобразования e^{-p Tn} = z^-1, то передаточная функция ЦВМ как дискретного звена равна K^*_цвм(p) = z^-α где 0 ≤ α ≤ 1.

За время T₀ = α T_n информация обрабатывается в соответствии с заложенными в машину алгоритмами, которые задаются в виде разностных уравнений. Если эти уравнения линейные, например вида (1.5) или (1.8), то алгоритму будет соответствовать передаточная функция K^*_α(z), которая в виде дискретного звена должна отображаться на структурной схеме.

Рис. 1. 24. Структурная схема цифровой следящей системы

Подводя итоги всему сказанному выше, можно представить структурную схему ЦСАУ в виде рис. 1.24, где суммирующими и нелинейными звеньями обозначен цифровой измеритель рассогласования, запаздывающим звеном z^-α - цифровая вычислительная машина, а дискретным звеном K^*_α(z) - линейный алгоритм обработки информации. Последовательное соединение запаздывающего и алгоритмического звеньев образует передаточную функцию линейной части ЦСАУ

K*(z) = z^-α K^*_α(z).

В том случае, когда период квантования T_n определяется только быстродействием ЦВМ, можно полагать α = 1, а если время обработки T₀ << T_n, то α = 0. Выбором достаточно большого числа разрядов цифрового кода можно сделать шаг квантования Δ и ошибку округления настолько малыми, что влиянием нелинейного звена можно пренебречь и считать ЦСАУ линейной дискретной системой.