Графическое изображения вариационных рядов распределения

Ряды распределения удобно анализировать при помощи их графического изображения, позволяющего судить и о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.

Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс (х) в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат (y) наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяются прямыми линиями, в результате этого получают ломаную линию, называемую полигоном распределения. Иногда для замыкания полигона предлагается крайние точки (слева и справа на ломаной линии) соединить с точками на оси абсцисс. В этом случае получается многоугольник. На оси ординат могут наноситься не только значения частот, но и частостей вариационного ряда.

В качестве примера (рис. 3.1) изобразим графически распределение жилого фонда по типу квартир (исходные данные – табл. 3.7).

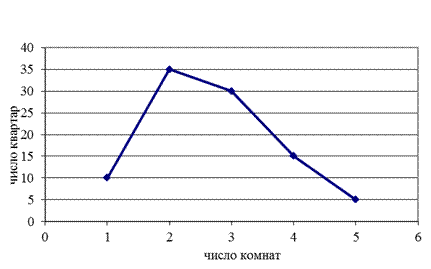
Рис. 3.1. Полигон распределения жилого фонда района N по типу квартир, 2013 г.

Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков в случае равных интервалов должна быть пропорциональна частотам. В результате мы получим гистограмму - график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.

В качестве примера (рис. 3.2) изобразим графически интервальный ряд распределения студентов по росту (исходные данные - табл. 3.8).

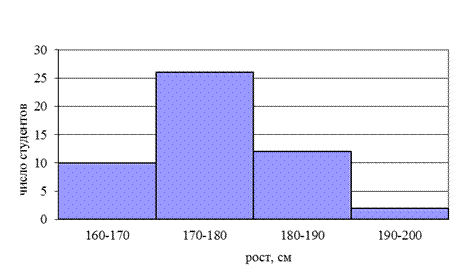
Рис. 3.2. Гистограмма распределения студентов по росту

Гистограмма может быть преобразована в полигон распределения, если найти середины сторон прямоугольников и затем эти точки соединить прямыми линиями (рис. 3.3).

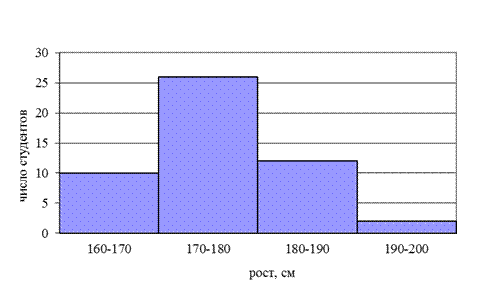
Рис. 3.3. Преобразование гистограммы в полигон распределения

При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах.

Для графического изображения вариационных рядов может также использоваться кумулятивная кривая. При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам и показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.

В качестве примера (рис. 3.4) изобразим графически кумуляту распределения студентов по росту (исходные данные - табл. 3.8).

Если в прямоугольной системе координат построим точки, ординаты которых – варианты, а абсциссы – накопленные частоты (или частости), а затем соединим их отрезками прямой, то получим ломаную линию, которая называется огивой (рис. 3.5).

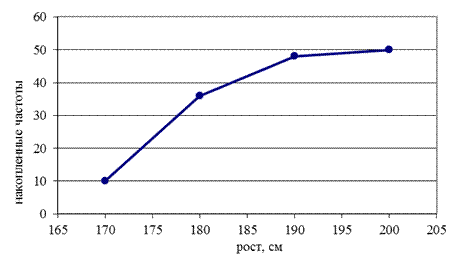
Рис. 3.4. Кумулята распределения студентов по росту

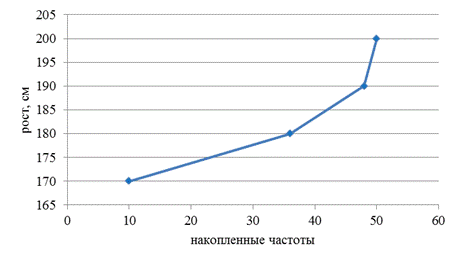
Рис. 3.5. Огива распределения студентов по росту

Широкое применение компьютеров в практической работе экономиста облегчает построение рядов распределения и их графическое представление.