Дополнительные материалы: Е2Е-проекты по системному анализу и моделированию

Данные проекты могут быть использованы как для обычной проектной работы (обучения), так в качестве тем для курсовых, дипломных проектов и научных исследований. Введем, по аналогии с B2B, P2P, С2С, мнемонический код E2E для обозначения "Экология для экономики" или "Экономика для экологии". Это обозначение может ассоциироваться также с системами типа "Электроника для экологии", или "Электроника для экономики", или "Электроника для эколого-экономического моделирования". Этот класс проблем наиболее важен для современного общества. Нижеследующие проекты предназначены для выработки навыков системного подхода и исследования, моделирования Е2Е-систем.

А. Цель проекта и этапы выполнения проекта:

1. изучение литературы общего (по системному анализу) и предметного характера (по рассматриваемой проблеме), выявление и описание элементов, целей, их приоритетов;
2. определение и описание ресурсов исследования (математических, предметных, программных, технических, технологических);
3. информационное обследование системы (сбор и изучение данных о системе, разработка необходимых спецификаций);
4. выбор и описание критериев адекватности, устойчивости, эффективности системы;
5. выбор метода (методов) и построение морфологической, функциональной и инфологической моделей системы;
6. выбор и описание критериев адекватности, устойчивости, эффективности, идентификации модели, на основе соответствующих критериев системы;
7. обсуждение и определение возможных критериев эффективности (полезности) принятия решений;
8. алгоритмизация и программирование;
9. отладка, тестирование, имитационные расчеты;
10. оформление проектного решения (отчета).

Б. Структура группы разработчиков:

1. постановщик проблемы - предметник (1 человек);
2. системный аналитик (1);
3. предметный аналитик (1-3, в зависимости от сложности выбранной системы);
4. системный программист (1);
5. прикладной программист (1-2);
6. специалист по тестированию, тестировщик (1);
7. специалист по презентациям (1);
8. приемная комиссия - эксперты, консультанты (1, 3 или 5).

Возможно совмещение функций.

В. Критерии оценки проекта: актуальность темы (системы), полнота, адекватность, информативность, качество и другие системные критерии.

С. Ориентировочный перечень проблем (темы могут быть выбраны и по желанию преподавателя и/или студента):

1. Прогноз поливов и величины урожая - важная социально-экономическая и сельскохозяйственная задача. Наиболее известные способы определения влажности почвы - метеорологический и термостатно-весовой. Первый может не дать желаемой точности, а второй связан с большими материальными и временными затратами. Поэтому важно разработать имитационную процедуру, дающую достаточную точность и учитывающую физиологические характеристики сельхозкультур. Уравнение водного баланса расчетного корнеобитаемого слоя растений можно записать: W'(t)=q(t)P(t)+P₁(t)-E(t)-(t), где P(t) - величина осадков; q(t) - коэффициент использования осадков (определяется, например, экспертно или по формуле Харченко С.И., через W_min - наименьшую влагоемкость почвы и W_z - влажность завядания); P₁(t) - подпитывание (приток) из грунтовых вод; E(t) - суммарное испарение из корнеобитаемого слоя; H(t) - уровень (сток) грунтовых вод, W(t) - средняя по слою влажность почвы (с учетом поливов или на межполивной период). Оценить и учесть влияние накопившейся к некоторому моменту времени биомассы растений на экологически обоснованную величину суммарного испарения в каждый момент времени. Величину суммарного испарения из корнеобитаемой зоны растений представить в виде суммы интенсивности транспирации растениями E₁(t) и интенсивности испарения с поверхности почвы E₀(t): E(t)=E₀(t)+E₁(t). Прирост биомассы описывается, например, уравнением x'(t)=a(t)E₁(t)-b(t)x(t), где x(t) - биомасса культуры; a(t) - эффективность транспирации; b(t) - коэффициент расхода на дыхание. Для определения динамики накопления биомассы может использоваться банк различных моделей, из которых подбирается по тем или иным критериям адекватности наилучшая модель (по результатам идентификации). В рассматриваемой нами процедуре моделирования будем использовать простую для идентификации модель Ферхюльста-Пирла: x'(t)=[ε(t)-λ(t)x(t)]x(t), где ε - коэффициент роста (автоприроста), λ - коэффициент сопротивления среды (нехватки воды). Динамика прироста биомассы хорошо описывается уравнением Давидсона-Филиппа: х'(t)=e₀(t)(F(t)-R(t)), где e₀ - коэффициент перехода от массы усвоенной СО₂ к сухой фитомассе; F - суммарный фотосинтез растений; R - суммарное дыхание растений. Интенсивность дыхания за сутки зависит от величины накопившейся биомассы. Экспериментально получено, что R(t)=b(t)x(t)+e₁F(t), где e₁ - коэффициент затрат на рост биомассы растений. Коэффициенты е₀, е₁ - экспериментально определяемые, для ряда культур ε₀=0,68, ε₁=0,27. Принимая во внимание приведенные уравнения и соотношения, имеем следующую модель расчета влажности почвы, с учетом динамики накапливаемой биомассы: W'(t)=q(t)P(t)+P₁(t)-E(t)-H(t), E₁'(t)=[ε(t)-λ(t)x(t)+b(t)]x(t)/a(t), Из этих соотношений имеем: b(t)=(1-e₁)F(t)/x(t)-(ε(t)-λ(t)x(t))/e₀. Для нахождения влажности почвы нам необходимо идентифицировать ε и λ. При постоянстве этих параметров (для простоты) можно использовать имитационную процедуру на основе метода наименьших квадратов:

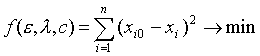
где i - номер фазы вегетации растения (i=1,2, ..., n); n - число фаз вегетации; x_i0 - экспериментальные величины урожайности культуры за репрезентативный период времени; x_i - теоретические величины урожайности сельхозкультур, определяемые по приведенной выше формуле. Фотосинтез F возможно учесть, например, с помощью формулы: F(t)=F_maxe^-μ[s(t)-z][λ(t)x(t)/ε(t)]^2/3, где s(t) - текущая сумма биологически активных температур, z - сумма биологически активных температур для максимального развития листовой поверхности, m - эмпирический коэффициент. Одним из наиболее важных условий увеличения урожайности сельхозкультур является необходимая влажность почвы, которая позволит получить оптимальный режим орошения и, как следствие, - высокий урожай. Определить проектную урожайность для сравнительно длительных промежутков времени (фаз вегетации):

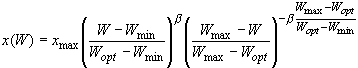
где x(W) - прогнозная урожайность; x_max - максимальная урожайность сельхозкультур; W - влагообеспеченность корнеобитаемого слоя почвы, определяется как описано выше; W_min, W_max - соответственно, нижняя и верхняя границы влагообеспеченности почвы, при которой урожай равен нулю; W_opt - влагообеспеченность, соответствующая x_max; β - параметр, характеризующий темпы роста урожая с увеличением влагообеспеченности.

2. Рассмотрим социо-эколого-экономическую проблему оценки степени загрязнения среды и воздействия загрязнителей на человека (животное, растение), а именно, интегральной оценки степени загрязненности среды для некоторых основных загрязнителей и оценки их влияния на человека и животное. При выборе загрязнителей учитываются: степень воздействия на экосистему; степень вредности (класс опасности) для человека; распространенность в биосфере; пороговый уровень содержания загрязнителя в атмосфере, при котором загрязнитель начинает свое воздействие; действие смеси загрязнителей, эффект суммирования воздействий. Например, для описанной ниже модельной ситуации были выбраны следующие загрязнители: сероводород, аммиак, двуокись углерода, двуокись азота, серная кислота, ацетон, двуокись серы, стирол, фтористый водород, окись углерода, этилацетат. Их выбор определялся как важностью для рассматриваемого объекта (гидрометаллургический объект), так и применением найденных открытых источников данных. С использованием многофакторного нелинейного анализа был получен ряд регрессионных зависимостей, а затем на их основе вычислены нормированные интегральные оценки загрязнения (приведенные к единице). Имитационная процедура строилась следующим образом. Пусть интегральная оценка загрязнения среды обозначается через y. Будем, для простоты, различать только 3 случая:

1. слабо выраженное загрязнение - 0 y⁽¹⁾<1/3;
2. средне выраженное загрязнение - 1/3 y⁽²⁾<2/3;
3. сильно выраженное загрязнение - 2/3 y⁽³⁾ 1.

Под у понимается некоторая интегральная характеристика, оценка суммарного воздействия загрязнителей, например, она может быть ассоциирована с вероятностью загрязнения; оценки y⁽¹⁾, y⁽²⁾ и y⁽³⁾ могут быть выражениями оптимистической, реалистической и пессимистической оценок загрязнения среды. Используя регрессионный и корреляционный анализ, получаем экспериментальные зависимости у_i=f(x_i), где x_i - фактор (загрязнителя) номер i, у_i - оценка загрязнения по x_i. Получены следующие результаты:

Номер фактора	Зависимость для человека	Зависимость для животного
	y=1,00000x	y=0,35714x
	y=0,0000029+1,17647x	y=0,09524x
	y=x/(0,0016+0,00007x)	y=x/(0,0014+0,00011x)
	y=2,10521x	y=1,11111x
	y=x/(0,0055+0,000068x)	у=x/(0,00666+1,00001x)
	Y=0,000013+0,351x	y=0,02857x
	y=x/(0,21+0,000115x)	y=0,02873x
	y=0,2941x	y=0,08x
	Y=0,0000991+2,41x	y=2,50x
	y=-0,00004+0,26317x	y=0,125x
	y=0,03634х	y=-0,00004+0,02778x

Остаточная дисперсия этих зависимостей не более 0,0001. Затем, используя эти зависимости в качестве базисных функций, в результате нелинейного регрессионного анализа по базисной системе {f_i} строятся зависимости вида y^(j)=F(y₁, y₂,..., y_n), j=1, 2, 3. При этом учитывается эффект суммирования влияния отдельных загрязнителей. Далее определяются оценки среднего ожидаемого загрязнения и его дисперсии для данной экологической системы. Приведенная процедура имитационного моделирования, при всей ее простоте, - технологична и позволяет оценивать загрязнение экосистемы, что актуально не только при экологическом, но и при социально-экономическом краткосрочном прогнозировании. Для слабо-, средне- и сильнозагрязненных участков (вдали, на среднем удалении, и вблизи от загрязнителя, например, от трубы гидрометаллургического завода) были получены зависимости для оценки интегрального влияния концентрации этих загрязнителей на человека:

y⁽¹⁾=exp(-1,79+2,89x₁+1732,87x₂+11002,4x₃+93,67x₄+1980,42x₅+1,58x₆+26,14x₇ +34,657x₈+42,001x₉+3,466x₁₀+0,046x₁₁)y⁽²⁾=exp(-0,81+0,58x₁+67,58x₂+2534,16x₃+0,92x₄+540,62x₅+0,34x₆+10,14x₇ +0,20x₈+8,11x₉+0,37x₁₀+0,02x₁₁)y⁽³⁾=exp(-0,02+0,01x₁+0,12x₂+6,28x₃+0,01x₄+1,83x₅+0,004x₆+0,05x₇ +0,003x₈+0,02x₉+0,003x₁₀+0,37x₁₁)

Для тестового примера (случай слабого загрязнения): х₁=х₂=х₃=0, х₄=х₅=х₆=х₇=0,0001, х₈=х₉=0,001, х₁₀=х₁₁=0,01 (мг/л) получаем оценку загрязненности этого имитационного полигона среды y⁽¹⁾=0,23. При этом, используя аналогичные оценки для случаев средне- и сильнозагрязненных участков, получим y⁽²⁾=0,56 и y⁽³⁾=0,98, что согласуется с вышеприведенными гипотетическими оценками, для которых строилась модель. Математическое ожидание загрязнения среды и дисперсия: М=0,57, σ=0,02. Отметим, что если все х_i=0 (i=1, 2, :, 11), то, например, y⁽¹⁾=0,09. Это может быть отражением как меры адекватности модели, так и, скорее всего, присутствием в среде фонового загрязнения даже при нулевом загрязнении, что подтверждают известные экологи (Р.Г. Хлебопрос). Из приведенного модельного примера видно, что модель может быть полезна для планирования экологических и эколого-экономических мероприятий, например, последствий (штрафов) за экологические нарушения. Обобщить, усложнить ситуацию и провести аналогичное исследование.

3. При исследовании ряда экологических и социально-экономических систем часто достаточно бывает качественно оценить воздействия, особенно наиболее существенные, и определить причинно-следственные связи между воздействиями (человека, например) и вектором х состояния системы, x=(x₁, x₂, ..., x_n), где х_i - фактор экологического состояния, i=1, 2,..., n. Такого рода модели не позволяют нам оценить всю сложную и динамическую цепь взаимовлияний экологических параметров среды, но являются когнитивным инструментарием на начальных стадиях исследования системы, например, на этапе формализации и структурирования системы. Рассмотрим следующую процедуру проведения экспертизы и основанного на ней моделирования. Сформируем профессиональную (эффективную качественно и количественно) группу экспертов. Требования к качественному составу: общая эрудиция; профессионализм в данной области; психологическая совместимость; научный интерес и отсутствие материального интереса к проблеме; опыт, умения и навыки; самокритичность и критичность. Обычно это осуществляется анкетным опросом, тестированием. Количественная оценка компетентности потенциального i-го эксперта:

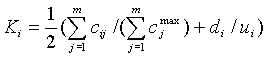
где c_ij - вес градации, перечеркнутой i-ым экспертом по j-ой характеристике в анкете, c_j^max - максимальный вес (предел шкалы) j-ой характеристики в баллах, m - общее количество характеристик в анкете, d_i - вес ячейки, перечеркнутой экспертом в шкале самооценки в баллах, u_i - предел шкалы самооценки эксперта в баллах. Оптимальная численность экспертной группы оценивается сложнее. Необходимо обеспечить высокий уровень компетентности экспертной группы и стабилизацию средней оценки прогнозируемой системы. Максимальная ее численность может быть оценена как

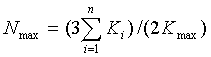
где K_max - максимально возможная компетентность в выбранной системе шкал, n - количество испытуемых. Минимальная численность может быть оценена как N_min=0,5(3/h+5), где h - допустимая величина изменения средней оценки в группе, при условии, что экспертная группа считается сформированной, если за нее голосовали не менее 2/3 испытуемых. Численность экспертной группы должна быть от N_min до N_max . После того, как экспертная группа сформирована, приступаем, собственно говоря, к процедуре моделирования. Выбирается, например, эмпирическим путем вектор состояния системы x Ω, Ω - рассматриваемая область (среда), а также некоторые граничные векторы состояния среды a=(a₁, a₂, ..., a_n), b=(b₁, b₂, ..., b_n), a_i=min{x_i}, b_i=max{x_i}, где минимум и максимум берется по всей области Ω. Составляется матрица V из элементов v_ij, где v_ij - степень влияния x_i на x_j, i=1,2,...,n. При этом можно использовать, например, подмодели корреляционного анализа. Далее выбираем начальное состояние х₀ и проводим имитационные расчеты по заданной временной сетке. Управление моделью (траекторией поведения системы) можно осуществлять изменениями параметров x_i, a_i, b_i, v_ij или выбором новой модели взаимодействия из некоторого банка моделей. Простыми моделями этого банка могут быть квадратичная, кубическая, дробно-рациональная, экспоненциальная, логарифмическая и другие зависимости. Используется также динамическое переупорядочивание связей в системе, модели (например, переход от одной модели к другой, более оптимальной по остаточной дисперсии). Наконец, оцениваем эффективность j-й траектории (имитационного варианта номер s, приводящего к решению номер r, 1 r R):

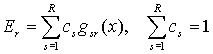
где N - число траекторий, c_s - экспертная оценка значимости цели номер s, g_sr(x) - функционал эффективности траектории s, приводящей к цели r. Определяем вероятность p_zk предпочтения траектории номер z другой траектории с номером k и функцию правдоподобия этого предпочтения W:

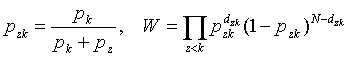
где p_z и p_k - вероятности предпочтений для траекторий номер z, k, соответственно, d_zk - экспертная (сравнительная) оценка траекторий z и k (ее можно взять, в частности, равной сумме оценок или баллов, при которых траектория z предпочиталась траектории k). Заметим, что более сложная и формализованная модель получается, если повторять имитационные расчеты с различными вероятностями p_z и p_k, уточняемыми каждый раз, например, следующим образом (q_z - экспертная оценка траектории z, например, сумма баллов, в которой отмечалась траектория номер z):

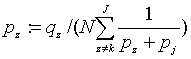
Данная процедура и ее модификации могут быть использованы при реализации экспертных систем в различных областях. Реализуйте данную процедуру в одной информационной системе (например, в экспертной системе).

4. В качестве конкретного примера реализации имитационных вычислительных экспериментов рассмотрим модель качественного прогнозирования системы (процесса). При решении многих Е2Е-проблем, когда из-за длительности экологических процессов экспериментальное изучение становится практически невозможным, построение математических и компьютерных моделей часто является единственным способом принятия ключевых решений. Для разрешения многих эколого-экономических задач достаточно качественно промоделировать динамику развития системы. В рассматриваемой системе (модели) ключевую роль играют факторы состояния системы. Так как при построении модели учесть все факторы влияния практически невозможно, то модель данного типа не позволяет проследить всю сложную цепь взаимовлияния экологических параметров среды, но с ее помощью становится возможным оценить наиболее существенные эколого-экономические воздействия, а также определить причинно-следственные связи в данной экосистеме. Для каждого определяющего фактора задается его текущее, максимальные и минимальные значения границ его изменения или задается вектор состояния экосистемы x=(x₁, x₂,...:, x_n) и два вектора границ его изменения: x^max=(x₁^max, x₂^max,..., x_n^max), x^min=(x₁^min, x₂^min,..., x_n^min), где n - число факторов. При этом для каждого фактора: x_i^min<x_i<x_i^max. Для каждого фактора задается коэффициент влияния его на каждый из остальных, в том числе и на самого себя, т.е. строится матрица воздействий A:

			...	n
	a11	a12	...	a1n
	a21	a22	...	a2n
...	...	...	...	...
n	an1	an2	...	ann

Матрица имеет порядок n, где n - число рассматриваемых факторов. Коэффициент a_ij показывает степень влияния фактора x_i на фактор x_j. При равном взаимном влиянии факторов, элементы матрицы можно брать как коэффициенты парной корреляции. В дальнейшем, по этой заданной матрице воздействия, на каждом временном шаге будет вычисляться новое состояние каждого фактора в зависимости от состояния других. Затем проводится формирование вектора состояния системы. При нормировании каждому фактору присваивается значение, лежащее от 0 до 1, которое зависит от максимального и минимального значений:

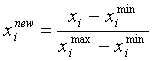
В различных системах факторы взаимосвязаны между собой различным образом. Определяет эту связь не только матрица воздействия, но и функциональная зависимость одного фактора от других. В данной модели для простоты использованы два основных метода взаимосвязи, а именно линейная и экспоненциальная зависимость (расширение банка функций не принципиально). Основным предназначением данной системы является проведение учебных имитационных экспериментов для получения данных, качественно характеризующих состояние экосистемы в заданный момент времени. В ходе эксперимента на экран выводятся графики, показывающие состояние каждого из факторов в тот или иной момент времени. На каждом временном шаге система вычисляет новое состояние каждого фактора. В зависимости от выбранной гипотезы взаимодействия факторов, выбираем зависимость вида f_i(x₁,x₂,...,x_n), например,

f_i(x₁,x₂,...,x_n)=a_1ix₁+a_2ix₂+...+a_nix_n

для линейной зависимости или

f_i(x₁,x₂,...,x_n)=exp(a_1ix₁+a_2ix₂+...+a_nix_n)

для экспоненциальной. Текущее состояние экосистемы можно представить точкой n-мерного пространства. В эксперименте экосистема пребывает во множестве таких точек, и совокупность их является траекторий развития системы. Управление экосистемой, траекторией ее развития, происходит при помощи изменения текущего состояния факторов, минимального и максимального их значений, редактирования матрицы влияния. Реализована возможность "записи и считывания экосистемы" в файл, что избавляет от необходимости каждый раз вводить параметры экосистемы. На экране отображается продолжительность эксперимента, факторы и приписываемая каждому фактору палитра цветов. После окончания эксперимента выводятся конечные значения факторов. Пользователь может сохранить их в отдельном файле для последующего использования. Реализовать соответствующую информационную систему прогнозирования.

5. Рассмотрим рынок жилья. Можно выделить два подхода к оценке жилья - использование математических и компьютерных оценок и использование экспертных оценок. В основе математической и компьютерной оценки лежит принцип статистической обработки большого массива объектов недвижимости и анализа зависимости цены объекта от его характеристик, таких как местоположение, износ, наличие улучшений и т.д. В процессе сбора данных поступает весьма разнородная информация. В случае неудовлетворительной адекватности производится корректировка модели путем изменения ее вида и введения новых переменных либо путем рекалибровки ее коэффициентов. Обычно набирается достаточное количество подобных объектов, и получаемый результат усредняется. Существует много статистических и моделирующих процедур для анализа рынка и построения модели, в частности, NCSS, AEP, Microcal Origin и др. Они достаточно сложны в использовании, хотя и предоставляют специалисту большие возможности. Имея хорошую базу данных, можно построить и настроить успешно работающую модель в течение 1-2 недель. Если же эксперту нужно разобраться в чужом рынке и начать выдавать приемлемые оценки, то среднее отклонение оценок рынка жилья по моделям относительно реальных цен не будет сильно отличаться от этой величины, причем эта оценка может выигрывать по среднему отклонению за счет фильтрации шумов во временных данных стоимости жилья. При условии достаточно полной, корректной и представительной базы данных, реальные и прогнозные средние примерно равны, и последние будут отражать наиболее вероятные цены сделок. С другой стороны, рыночная стоимость никогда не определена абсолютно точно, существует вариация стоимости каждого конкретного объекта и, соответственно, средняя вариация по базе. Моделирование рынка жилья, как правило, подстегивает инвестиции в недвижимость. В предлагаемой процедуре моделирования предпринята попытка анализа рынка жилья г. Нальчика и построения экономико-статистических оценок рынка. К сожалению, из-за отсутствия реальных данных по объему и ценам сделок, рынок пришлось моделировать на основе данных, полученных путем анализа объявлений в газетах "Синдика-Информ" и "Из рук в руки". Такие данные достаточно приблизительны и дают возможность анализа лишь предложения на рынке жилья, но этот подход вкупе с математическим и компьютерным анализом данных может оказаться одним из эффективных приемов при оценке качественного и среднестатистического состояния рынка жилья. При наличии данных не представляет трудностей переход и к проблеме анализа цен и спроса на рынке жилья. Цена на жилье зависит от ряда объективных качественных параметров, к которым можно отнести: месторасположение и время постройки дома; количество комнат; смежность комнат; общая площадь; жилая площадь; площадь кухни; этаж; этажность дома; материал стен; наличие балконов и лоджий; наличие телефона; удаленность от центра города; расположение относительно станций ж/д и автомагистралей; расположение относительно центров локального влияния (места работы); дата оценки. Цены на жилье в г. Нальчике сравнимы с ценами многих курортных и промышленных центров России. Материальную основу жилищного рынка в КБР составляет приватизированное жилье г. Нальчика. По данным различных источников в КБР, доля приватизированных квартир составляет 55 %, что близко к данным по Ставропольскому краю (56%), Ростовской области (51%), Северной Осетии - Алании (54%). Так как использовалась методика сбора данных по газетным объявлениям, необходимо было до компьютерного анализа (построения моделей) осуществить предварительную статистическую обработку. Простая процедура предварительной статистической обработки такова:

1. Вычисляются средние величины x₀ по 1, 2, 3, 4-комнатным квартирам.
2. Вычисляются наибольшее x_max и наименьшее x_min в каждой из групп.
3. Вычисляются наибольшие отклонения от среднего в каждой группе (или размах): d_max=| x_{min (max)} - x₀|.
4. Вычисляются относительные отклонения: w=d_max /x₀ .
5. Находим по таблице Стьюдента процентные точки для t(5%) и t(0,1%).
6. Вычисляем соответствующие точки w(5%; n), w(0,1%; n).
7. Если w(5%; n)>t(5%) (w(0,1%; n)>t(0,1%)), то отсеиваем грубое значение цены жилья и пересчитываем все заново (повторяем п.1-7).

По результатам, полученным после работы этого алгоритма, было проведено математическое и компьютерное моделирование по нахождению регрессионных зависимостей наилучшей адекватности вида: x=x(t), y=y(t), где x - оценка ($) стоимости 1 м² жилья общей площади; y - оценка стоимости 1 м² жилья жилой площади; t - время: t=1 - январь, t=2 - февраль и т.д. В результате проведенных достаточно громоздких и объемных расчетов (не приводимых по этой причине) выявлено, что наиболее адекватной формой модели является обратно-пропорциональная зависимость:

x(t)=1/(At+B), y(t)=1/(Ct+D),

где регрессионные параметры A, B, C, D определяются на основе экспериментальных данных с использованием метода наименьших квадратов и линеаризующих замен:

X(t)=1/x(t), Y(t)=1/y(t).

В результате такой замены обратно-пропорциональная зависимость линеаризуется, т.е. приводится к виду:

X(t)=At+B, Y(t)=Ct+D.

Далее, в соответствии с методом наименьших квадратов, находим неизвестные A, B, C, D. После нахождения решений A, B, C, D можно осуществить обратную замену в обратно-пропорциональных зависимостях и найти регрессионные зависимости вида (с оценкой адекватности): x=x(t), y=y(t). Получены в результате моделирования адекватные модели регрессионного типа. Оценки адекватности этих моделей примерно равны 10^-6 (остаточная дисперсия). Приведем ряд построенных моделей. Модель оценки средней стоимости 1 м² общей площади по всем типам квартир по 1997-1998 годах: x(t)=1/(0,0044-0,00006 t). Модель средней стоимости 1 м² жилой площади по всем типам квартир по 1997-1998 годах: x(t)=1/(0,0018-0,0009 t). Для сравнительного анализа и оценки адекватности модели были проделаны соответствующие расчеты по более точным данным риэлторских групп Москве. Были получены, соответствующие модели: x(t)=1/(0,000008 t+0,00098); y(t)=1/(0,000006 t+0,00061). Итак, наилучшей формой зависимостей при моделировании рынков жилья гг. Москвы и Нальчика (возможно, и других) является зависимость

x(t)=(a+bt)^-1 , y(t)=(c+dt)^-1 .

Полученные модели можно использовать для прогнозных расчетов. Например, используя полученную для стоимости 1 м² общей площади жилья г. Москвы формулу, можно рассчитать значение на февраль 1998 года (берем t=26):

x(26)=1/(0,000008×26+0,00098)=1/0,001188=941,75 ($).

Это достаточно близко к данным риэлторских групп г. Москвы на февраль 1998 года - 957$. Отклонение составляет 1,5 %, модель приемлема. Необходимо проделать вышеприведенную работу (информационное обследование рынка жилья в Вашем городе и сбор данных, выполнение приведенной или более "тонкой" процедуры предварительной обработки, регрессионный анализ) для рынка жилья Вашего города.

6. Пусть относительное число лиц, желающих поменять свой Е2Е-выбор номер 1 на выбор номер 2 пропорционально числу x₁ тех, кто уже сделал выбор 1 и относительной привлекательности выбора 2, т.е. числу a₂x₁/(a₁+a₂). Аналогично, число лиц, желающих поменять свой выбор 2 на выбор 1, будет пропорционально числу a₁x₂/(a₁+a₂). Если k₁ и k₂ - указанные коэффициенты пропорциональности, то можно записать модель динамики выбора решений из двух возможных:

x'₁(t)=k₁x₁(a₁x₂/(a₁+a₂)-a₂x₁/(a₁+a₂)), x₁(0)=x₁₀ ,x'₂(t)=k₂x₂(a₂x₁/(a₁+a₂)-a₁x₂/(a₁+a₂)), x₂(0)=x₂₀ .

На выбор решения влияют различные факторы. Осуществить системный анализ этих факторов для некоторой выбранной Вами Е2Е-системы, построить соответствующую модификацию приведенной выше модели с "расщеплением" параметров модели (например, для простоты рассуждений, аддитивно), выполнить жизненный цикл моделирования с целью: а) выработки тактики увеличения (уменьшения) k₁ и k₂; б) идентификации параметров k₁ и k₂.

7. Популяцию рассматривают в качестве структурной единицы вида и единицы эволюции. Каждая популяция характеризуется определенной численностью (частотой, процентом или долей) особей с тем или иным признаком, ее изменениями во времени. В природе происходит постоянное колебание численности популяций: число особей то сокращается, то увеличивается. Неравномерность распределения особей одного вида в ареале обитания связана с колебаниями урожаев кормов, климатических условий (влажность, температура, освещенность), возрастным и половым составом особей, интенсивностью их размножения и продолжительностью жизни. К факторам эволюции, помимо естественного отбора - процесса, в результате которого выживают и оставляют после себя потомство преимущественно особи с полезными в данных условиях признаками, - относится также изоляция, т.е. возникновение различных преград к свободному скрещиванию особей. Перечисленные факторы повышают или понижают частоту различных генотипов в популяции и значительно усложняют зависимости в уравнении эволюции. Сокращение численности за некоторые пределы может привести к вымиранию генотипов популяции или к стационарности плотности особей. Пусть популяция состоит из трех генотипов с частотами x, y, z. Будем считать, что действует только естественный отбор, и вероятности доживания особей до репродуктивного возраста каждого генотипа определяются, соответственно, как a, b, c. Уравнения эволюции можно взять в виде

x_i+1=x_i+x_i(a-ax_i-by_i-cz_i), x_o=d,y_i+1=y_i+y_i(b-ax_i-by_i-cz_i), y₀=e,z_i+1=z_i+z_i(c-ax_i-by_i-cz_i), z₀=m.

Вероятности a, b, c, d, e, m можно задавать (как численно, так и с помощью функции распределения вероятностей) или генерировать датчиком случайных чисел. Осуществить системный анализ аналогичной Е2Е-системы, построить соответствующую модификацию приведенной выше модели, выполнить жизненный цикл моделирования с целью а) вычисления численности генотипов в каждый момент времени; б) определения, происходит ли вымирание особей каждого генотипа или же возникает ли момент, когда численность особей каждого генотипа становится стационарной; г) определения вероятности дожития особей до репродуктивного возраста; д) выяснения, как можно использовать эту систему (исследования) в пенсионном или страховом деле, например, для расчета страхового риска.

8. Рассмотрим базу знаний и экспертную Е2Е-системы с использованием аппарата нечетких множеств и нечеткой логики, которая позволит оценивать (в том числе - качественно) социо-экономико-экологическое состояние некоторой среды по задаваемым пользователем (экспертом) количественным оценкам тех или иных параметров среды (выбираемых из базы знаний системы). Для каждого входного фактора в диалоговом режиме задаются относительные (от 0 до 1) оценки влияния этого фактора (вес фактора). После анализа этих данных (этой экологической обстановки) система принимает, на основе базы знаний, решение о состоянии социо-экономико-экологической среды, используя количественную оценку (от 0 до 1) и десятибалльную (0-9) качественную систему оценок. Для автоматического получения базы знаний используется алгоритм классификации заданного класса. Пусть имеется набор объектов, которые необходимо разделить на группы. Определяется функция f(x,y) принадлежности нечеткого отношения типа "сходство" на заданном множестве объектов (для каждой пары объектов x, y). По этой функции определяется обычное (не нечеткое) отношение на множестве объектов, по которому эти объекты разбиваются на классы эквивалентности (классы, в которые попадают только элементы, эквивалентные по данному отношению). Для создания базы знаний (какого типа?) и обучения можно использовать процедуру вида: