Основы алгебры и логики

При записи тех или иных логических выражений используется специальный язык, который принят в математической логике. Основоположником мат логики является великий немецкий математик Готфрид Вильгельм Лейбниц(1646-1716). Он сделал попытку построить универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычислений. На заложенном Лейбницем фундаменте ирландский математик Джордж Буль построил здание новой науки – матлогики, - которая в отличие обычной алгебры оперирует не числами, а высказываниями.

Алгебра логики – это раздел математической логики, значения всех элементов которой определены в двух элементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями.

Высказывание – это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. Каждое высказывание или истинно или ложно и не может быть одновременно и истинным, и ложным.

Операции в алгебре логики:

· Логическое сложение (операция ИЛИ, дизъюнкция)

· Логическое умножение (операция И, конъюнкция)

· Логическое отрицание (операция НЕ, инверсия)

Логическая операция НЕ является унарной, т.е. имеет всего 1 операнд.

Х	NOT X

Операции И и ИЛИ являются бинарными, представляют собой результаты действий над двумя логическими величинами.

X	Y	X and Y	X or Y

Задание: Дополнительные логические операций.

Операции И,ИЛИ,НЕ образуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение.

Условные обозначения базовых логических элементов:

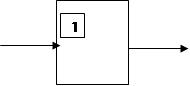НЕ И ИЛИ

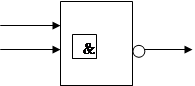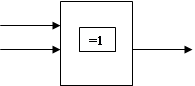И-НЕ исключающее ИЛИ

На практике логические элементы могут иметь не один или два, а значительно большее число входов.

Примем к сведению, что простейшие логические элементы, изображенные на рисунке, можно реализовать аппаратно. Это означает, что можно создать электронные устройства на транзисторах, резисторах и т.п. На практике логическому ДА соответствует наличие напряжения, логическому НЕТ – отсутствие.

Любую достаточно сложную логическую функцию можно реализовать с помощью простых логических операции.

Логические машины : триггер – основа устройств оперативного хранения информации, сумматор – служит для сложения чисел.

Булева алгебра логики - это алгебра, состоящая из нулей и единиц; или истины (TRUE)и лжи (False). В программировании булева алгебра логики встречается очень часто. Например, при создании различных управляющих структур (if , while , for ).