Определение прямоугольных координат
Прямая геодезическая задача
В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.1), горизонтальное расстояние SAB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол αAB или румб rAB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.
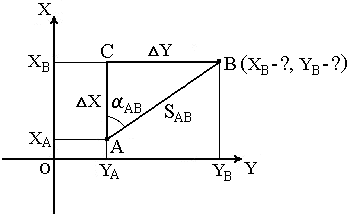
Рис. 1. Прямая геодезическая задача
Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.
Дано: Точка А( XA, YA), SAB и αAB.
Найти: точку В( XB, YB).
Непосредственно из рисунка имеем:
ΔX = XB– XA;
ΔY = YB– YA.
Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:
ΔX = SAB · cos αAB ;
ΔY = SAB · sin αAB .
Так как в этих формулах SAB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cosαAB и sinαAB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.
Таблица 1.
Знаки приращений координат ΔX и ΔY
| Приращения координат | Четверть окружности в которую направлена линия | |||
| I (СВ) | II (ЮВ) | III (ЮЗ) | IV (СЗ) | |
| ΔX | + | – | – | + |
| ΔY | + | + | – | – |
При помощи румба приращения координат вычисляют по формулам:
ΔX = SAB · cos rAB ;
ΔY = SAB · sin rAB .
Знаки приращениям дают в зависимости от названия румба.
Вычислив приращения координат, находим искомые координаты другой точки:
XB= XA + ΔX;
YB= YA + ΔY.
Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.
Обратная геодезическая задача
Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA) и В( XB, YB) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB(рис.2).
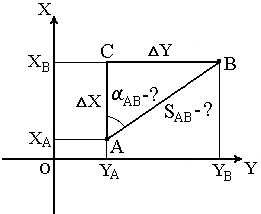
Рис. 2. Обратная геодезическая задача
Данная задача решается следующим образом.
Сначала находим приращения координат: 0о 19' 18"
ΔX = XB – XA;
ΔY = YB – YA.
Величину угла rAB определем из отношения
| ΔY | = tg rAB |
| ΔX |
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB.
Для контроля расстояние SAB дважды вычисляют по формулам:
| SAB = | ΔX |
| cos αAB |
| SAB = | ΔY |
| sin αAB |
Расстояние SAB можно определить также по формуле
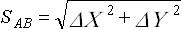 .
.
Определение прямоугольных координат.
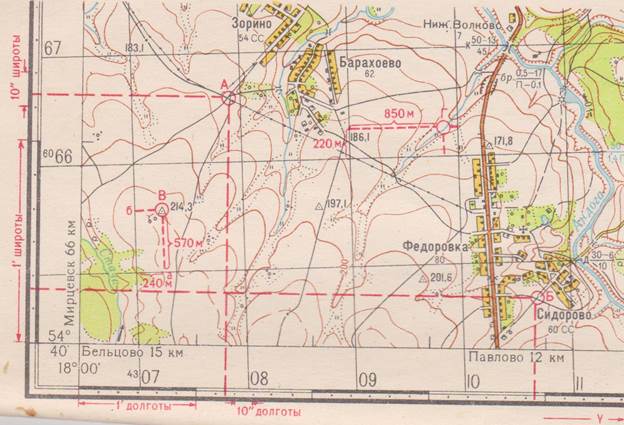
При определении координат точки В, сначала записывают абсциссу нижней километровой линии квадрата, в котором находится точка В, т.е. 6065км, где - 60 номер зоны (зоны подписывают только в начале и конце осей, чтобы не перегружать карту информацией), 65 - номер километровой линии. Измеряют расстояние аВ и пользуясь масштабом карты, определяют, чему оно равно на местности. Полученную величину 570м складывают с величиной абсциссы линии. ХВ = 6065000м+ 570м =6065570м
Аналогичным путем определяют ординату точки В. Записав значение ординаты левой стороны квадрата 4307км ( где - 43 номер зоны, 07 - номер километровой линии), к нему прибавляют длину линии бВ на местности - 240 м. Y = 4307000м + 240м =4307240м
ТЕМА1.4.
Решение обратной геодезической задачи. Сводная таблица.
I. Определить прямоугольные координаты ∆123
Х1=
Y1=
Х2=
Y2=
Х3=
Y3=
I I. Обратная геодезическая задача
Пример:
| Сторона 1-2 | Сторона 2-3 | Сторона 3-1 | ||
| Координаты углов зданий | Х2 | |||
| Координаты теодолитного хода | Х1 | |||
| ΔХ = Х2 - Х1 | ΔХ | -500 | -100 | |
| Координаты углов зданий | Y2 | |||
| Координаты теодолитного хода | Y1 | |||
| ΔY = Y2 - Y1 | ΔY | -1650 | ||
| ΔY / ΔX | tg r | 0,3333 | -2,9000 | 16,5000 |
| arctg ΔY / ΔX | r (о) | 0,3218 | -1,2387 | 1,5103 |
| Направление румба | r (о ' ") | СВ 0о 19' 18" | ЮВ 1о 14' 19" | ЮЗ 1о 30' 37" |
| Дирекционный угол | α (о ' ") | 0о 19' 18" | 178о 45' 41" | 181о 30' 37" |
| cos r | cos r | 0,9487 | 0,3260 | 0,0605 |
| sin r | sin r | 0,3162 | -0,9454 | 0,9982 |
| ΔX / cos αAB | SAB | 632,4555 | 1533,7862 | 1653,0275 |
| ΔY / sin αAB | SAB | 632,4555 | 1533,7862 | 1653,0275 |
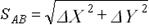 | SAB | 632,4555 | 1533,7862 | 1653,0275 |
Длины линий не имеют отрицательных значений!
III. Сводная таблица данных.
| Сторона 1-2 | Сторона 2-3 | Сторона 3-1 | |
| Dчисл | |||
| Dлиней | |||
| Dпопер | |||
| Dвычисл | |||
| αизмер | |||
| α вычисл |
Указать размерности данных.
| Dчисл - длина стороны измеренная с помощью численного масштаба (ПР/Р № 1) |
| Dлиней - длина стороны измеренная с помощью линейного масштаба (ПР/Р № 1) |
| Dпопер - длина стороны измеренная с помощью поперечного масштаба (ПР/Р № 1) |
| Dвычисл - длина стороны вычисленная - обратная геодезическая задача (ПР/Р № 4) |
| αизмер - дирекционный угол измеренный (ПР/Р № 3) |
| α вычисл - дирекционный угол вычисленный - обратная геодезическая задача (ПР/Р № 4) |
Написать вывод о расхождения вычисленных и измеренных значений.
