Однородные координаты точки

Однородными координатами точки М называется любая тройка одновременно неравных нулю чисел (X₁,X₂,h), связанных с заданными величинами х и у следующими соотношениями:

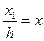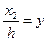Пусть М - произвольная точка плоскости с координатами (х, у), вычисленными относительно заданной прямолинейной координатной системы (рис.66).

Рис. 66

Применение однородных координат оказывается удобным уже при решении простейших задач.

Рассмотрим, например, вопросы, связанные с изменением масштаба чисел. Если устройство отображения работает только с целыми числами, то для точки с координатами (0.5, 0.1) можно ввести однородные координаты, выбрав значение h=10 и, тем самым привести координаты точки к виду (5, 1, 10).

Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами (80000, 1000) можно взять, например, h=0.001. В результате получим (80, 1).

Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям.

При помощи троек однородных координат и матрицы третьего порядка, считая h=l, общее аффинное преобразование можно записать следующим образом:

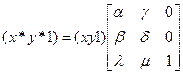Элементы матрицы произвольного аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому, чтобы реализовать то или иное отображение, то есть найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи и с описанными выше частными случаями разбивают на отдельные этапы.

На каждом этапе ищется матрица, соответствующая тому или иному из выделенных выше случаев А, Б, В или Г, обладающих хорошо выраженными геометрическими свойствами. Затем эти матрицы перемножаются.

Выпишем соответствующие матрицы третьего порядка.

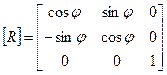А. Матрица вращения (rotation)

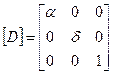Б. Матрица растяжения (сжатия) (dilatation)

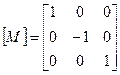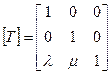В. Матрица отражения (относительно оси абсцисс) (reflection)

Г. Матрица переноса (translation)

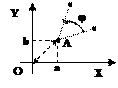Пример. Построить матрицу поворота вокруг точки А(a, b)на угол φ.

Рис.67

1-й шаг. Перенос на вектор А(-а, -b) для совмещения центра поворота с началом координат.

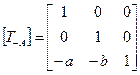2-й шаг. Поворот на угол φ.

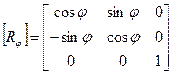3-й шаг. Перенос на вектор А(а, b) для возвращения центра поворота в прежнее положение.

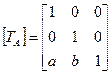Перемножим матрицы в том же порядке, как они выписаны:

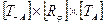В результате получим, что искомое преобразование (в матричной записи) будет выглядеть следующим образом:

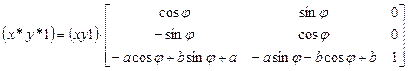Элементы полученной матрицы (особенно в последней строке) не так легко запомнить. В то же время каждая из трех перемножаемых матриц по геометрическому описанию соответствующего отображения строится достаточно легко.