Содержательный подход
Часть 1
Теоретические материалы.
В предметной области информатики выделяют две составляющие: научная (теоретическая) и прикладная (технологическая)
Тема 1: Математические основы информатики.
Понятие информации.
Информация (от лат. informatio — разъяснение, изложение, осведомлённость) — одно из наиболее общих понятий науки, обозначающее некоторые сведения, совокупность каких-либо данных, знаний и т.п. С точки зрения материалистической философии — это отображение реального мира с помощью сведений(сообщений). Сообщение-это форма представления информации в виде речи, текста, изображения, цифровых данных, графиков, таблиц и т.д. В широком смысле «информация» - это общенаучное понятие, включающее в себя обмен сведениями между людьми, обмен сигналами между живой и неживой природой, людьми и устройствами.
Информация – сведения об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, которые уменьшают имеющую степень неопределенности, неполноты знаний.
С практической точки зрения информация всегда представляется в виде «сообщения». Информационное сообщение связано с «источником информации», «приёмником информации» и «каналом передачи».
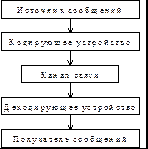
Сообщение от источника к приёмнику передаётся в материально-энергетической форме (электрический, звуковой, световой сигналы и т.п.). Человек воспринимает сообщения посредством органов чувств. Приёмники информации в технике воспринимают сообщения с помощью различной измерительной и регистрирующей аппаратуры.
Измерение информации.
Содержательный подход .
Количество информации, заключенное в сообщении, определяется объемом знаний, который несет это сообщение получающему его человеку. Сообщение содержит информацию для человека, если заключенные в нем сведения являются для этого человека новыми и понятными и, следовательно, пополняют его знания.
Если учитывать смысловое содержание сообщение, то при таком подходе возможна качественная оценка информации: полезная, безразличная, важная, вредная. … Одну и ту же информацию люди могут оценить по-разному. В информатике очень важно количественно измерять информации, найти числовой эквивалент полученного сообщения, т.к. информатика по определению изучает все аспекты сбора, хранения, обработки, передачи и получения информации. Естественно, это требует оценка и учета количества передаваемой информации, ее объема.
Количеством информации называют, числовую характеристику сигнала, которая не зависит от его формы и содержания и характеризует степень неопределенности (энтропии), которая исчезает после выбора (получения) сообщения в виде данного сигнала.
Поясним эту идею на конкретных примерах. Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет одно из двух возможных событий — монета окажется в одном из двух положений: «орел» или «решка». (можно говорить, что события равновероятны, если при возрастающем числе опытов число выпадений «орла» и «решки» постепенно сближаются, например, если мы бросим монету 10 раз, то «орел» может выпасть 7 раз, а «решка» — 3 раза, если бросим монету 100 раз, то «орел» может выпасть 60 раз, а «решка» — 40 раз, если бросим монету 1000 раз, то «орел» выпадет 520 раз, а «решка» — 480 и т.д., т.е. при очень большой серии опытов количество выпадений «орла» и «решки» сравняются).
Перед броском существует неопределенность нашего знания (возможны два события), и как упадет монета — предсказать невозможно. После броска наступает полная определенность, так как мы видим (получаем зрительное сообщение), что монета в данных момент времени находится в определенном положении (например, «орел»). Это сообщение уменьшило степень неопределенности в два раза, т.к. из двух возможных равновероятных событий реализовалось одно.
В окружающей действительности достаточно часто встречаются ситуации, когда может произойти большее, чем два, число равновероятных событий. Так, при бросании равносторонней четырехгранной пирамиды существует 4 равновероятных события, а при бросании шестигранного игрального кубика — 6 равновероятных событий.
Чем больше начальное число возможных равновероятных событий, тем больше начальная неопределенность нашего знания и, соответственно, тем большее количество информации будет содержать сообщение о результатах опыта.
