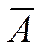Логическое отрицание (инверсия)
Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией.
Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное – истинным.
Пусть А= «2х2=4» истинное высказывание, тогда высказывание F, образованное с помощью операции логического отрицания, «2х2=4» - ложно.
Таблица истинности имеет вид:
Таблица 3
| A | F= 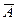 |
Читается «не А», или «А с чертой», или «отрицание А». Обозначается 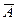 . Графическое изображение функции представлено на рис. 3.
. Графическое изображение функции представлено на рис. 3.
|
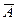
 |  |

Рис. 3.Инверсия.
Логические выражения и функции.
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составных высказываний в виде логических выражений на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Имеем логическое выражение составного высказывания «2х2=5 или 2х2=4 и 2х2¹5 или 2х2¹4». Оно состоит из простых высказываний:
А = «2х2=5 – ложно (0),
В = «2х2=4 – истинно (1).
Тогда составное высказывание можно записать в следующей форме:
«А или В и 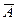 или
или 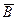
Теперь необходимо записать высказывание в виде логического выражения с учетом последовательности выполнения логических операций. При выполнении логических операций определен следующий порядок их выполнения: инверсия, конъюнкция, дизъюнкция. Для изменения указанного порядка используются скобки.
F = (AvB)&( 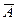 v
v 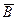 )
)
Истинность или ложность составных высказываний можно определить чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний. Для указанного выше логического выражения подставим значения переменных и руководствуясь таблицами истинности базовых логических операций имеем:
F = (AvB)&( 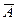 v
v 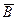 ) = (0v1)&(1v0) = 1&1 = 1
) = (0v1)&(1v0) = 1&1 = 1
Для данного составного высказывания построим таблицу истинности таблица 4), которая определяет его истинность или ложность при всех возможных комбинациях исходных значениях простых высказываний (логических переменных). При построении таблиц истинности необходимо руководствоваться определенной последовательностью действий:
1. Необходимо определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных n, то количество строк
N = 2n
В представленном примере логическое выражение F = (AvB)&( 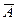 v
v 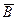 ) имеет две переменные А и В, следовательно
) имеет две переменные А и В, следовательно
N = 22 = 4
2. Необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций. В нашем случае количество переменных равно 2, количество логических операций равно 5, следовательно, должно быть семь столбцов.
3. Необходимо построить таблицу истинности с необходимым количеством строк и столбцов и внести возможные наборы значений исходных логических переменных.
4. Заполнить таблицу по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с таблицами истинности.
В итоге таблице истинности для указанного выше выражения будет иметь следующий вид:
Таблица 4
| А | В | AvB | 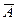 | 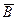 | 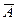 v v 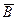 | (AvB)&( 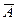 v v 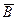 ) ) |