Алгоритм метода крутого восхождения
Начальный этап. Выбрать начальную точку X0(1)=[ 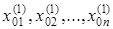 ]T, интервал варьирования DX(1)=[Dx1(1), D x2(1),…, Dxn(1)]Tи e> 0 - скаляр, используемый в критерии остановки,a - коэффициент сжатия шага, n–размерность задачи, число опытов равно N=2n. Положить k=1, i=1 и перейти к основному этапу.
]T, интервал варьирования DX(1)=[Dx1(1), D x2(1),…, Dxn(1)]Tи e> 0 - скаляр, используемый в критерии остановки,a - коэффициент сжатия шага, n–размерность задачи, число опытов равно N=2n. Положить k=1, i=1 и перейти к основному этапу.
Основной этап. Шаг 1. Вычислить натуральное и кодированное значение переменной х(k)i= 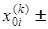 Dxi(k) и Yi=(xi(k)-x0i(k))/Dxi(k). Если i=n, то положить j=1 и перейти к шагу 2, иначе положить i=i+1 и вернуться к шагу 1.
Dxi(k) и Yi=(xi(k)-x0i(k))/Dxi(k). Если i=n, то положить j=1 и перейти к шагу 2, иначе положить i=i+1 и вернуться к шагу 1.
Шаг 2. В соответствии с матрицей планирования полного факторного эксперимента реализовать полный факторный эксперимент в окресности точки X(k). Определить значение функции f(Хj(k)). Если j=N, то положить i=1, j=1 и перейти к шагу 3, иначе вернуться к шагу 2.
Шаг 3. Вычислить коэффициенты аппроксимационного уравнения  f(X(k)) = b0(k) + b1(k)x1(k) + b2(k)x2(k) + … + bn(k)xn(k) по формуле
f(X(k)) = b0(k) + b1(k)x1(k) + b2(k)x2(k) + … + bn(k)xn(k) по формуле 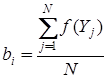 . Если i=n, то перейти к шагу 4, иначе вернуться к шагу 3.
. Если i=n, то перейти к шагу 4, иначе вернуться к шагу 3.
Шаг 4. Определить значение функции в точке (X(k)- jDX(k)Ba), если
f(X(k)- jDX(k)Ba)<f(X(k)), то положить j=j+1 и вернуться к шагу 4, иначе
X(k+1)= (X(k)- jDX(k)Ba), k=k+1 и перейти к шагу 5.
Шаг 5. Если ||X(k+1) - X(k)|| < e, то остановиться; в противном случае i=j=1и перейти к шагу 1.
Пример расчета экстремума функции методом крутого восхождения.
Постановка задачи. Найти минимум функции f(x) = (x1 - 2)4 + (х1 - 2х2)2. Выбираем начальное приближение Х(1) = [2.5; 2.5]Т, интервал варьирования на первой итерации принимаем DX(1)=[0.5; 0.5]T, a(1)=0,05 и точность поиска e=0,01.
Результаты расчетов минимума функции методом крутого восхождения с использованием табличного процессора EXCEL для данного варианта представлены в таблице 2.8. Траектория поиска метода приведена на рис.2.8.
Таблица 2.8.
Результаты расчета минимума функции f(x) = (x1 - 2)4 + (х1 - 2х2)2 методом крутого восхождения.
| 1. Эксперимент в точке [2.5,2.5], Δx1=0.5, Δx2=0.5, | ||||||||||||||
| № | Y1 | Y2 | x1 | x2 | f(X) | b1 | b2 | |||||||
| -1 | -1 | 2.00 | 2.00 | 4.00 | -2.00 | 5.00 | ||||||||
| -1 | 3.00 | 2.00 | 2.00 | a=0.05 | ||||||||||
| -1 | 2.00 | 3.00 | 16.00 | |||||||||||
| 3.00 | 3.00 | 10.00 | ||||||||||||
| Движение в направлении градиента | ||||||||||||||
| № | x1 | x2 | f(X) | № | x1 | x2 | f(X) | |||||||
| 2.500 | 2.500 | 6.3125 | 2.800 | 1.750 | 0.8996 | |||||||||
| 2.600 | 2.250 | 3.7396 | 2.900 | 1.500 | 0.6661 | |||||||||
| 2.700 | 2.000 | 1.9301 | 3.000 | 1.250 | 1.2500 | |||||||||
| 2. Эксперимент в точке [2.9,1.5], Δx1=0.5, Δx2=0.5, | ||||||||||||||
| № | Y1 | Y2 | x1 | x2 | f(X) | b1 | b2 | |||||||
| -1 | -1 | 2.40 | 1.00 | 0.1856 | 1.81 | 0.20 | ||||||||
| -1 | 3.40 | 1.00 | 5.8016 | a=0.1 | ||||||||||
| -1 | 2.40 | 2.00 | 2.5856 | |||||||||||
| 3.40 | 2.00 | 4.2016 | ||||||||||||
| Движение в направлении градиента | ||||||||||||||
| № | x1 | x2 | f(X) | № | x1 | x2 | f(X) | |||||||
| 2.900 | 1.500 | 0.6661 | 2.538 | 1.460 | 0.2296 | |||||||||
| 2.719 | 1.480 | 0.3255 | 2.358 | 1.440 | 0.2893 | |||||||||
| 2. Эксперимент в точке [2.538,1.460], Δx1=0.75, Δx2=0.5, | ||||||||||||||
| № | Y1 | Y2 | x1 | x2 | f(X) | b1 | b2 | |||||||
| -1 | -1 | 1.788 | 0.960 | 0.0193 | 0.80 | 0.76 | ||||||||
| -1 | 3.288 | 0.960 | 4.6280 | a=0.1 | ||||||||||
| -1 | 1.788 | 1.960 | 4.5457 | |||||||||||
| 3.288 | 1.960 | 3.1544 | ||||||||||||
| Движение в направлении градиента | ||||||||||||||
| № | x1 | x2 | f(X) | № | x1 | x2 | f(X) | |||||||
| 2.538 | 1.460 | 0.2296 | 2.217 | 1.155 | 0.0108 | |||||||||
| 2.458 | 1.384 | 0.1397 | 2.136 | 1.078 | 0.0008 | |||||||||
| 2.378 | 1.307 | 0.0766 | 2.056 | 1.002 | 0.0027 | |||||||||
| 2.297 | 1.231 | 0.0350 | Критерий | Достигнут | ||||||||||


 В результате трех итераций реализации метода крутого восхождения получена точка Х*=[2.056; 1,002]т, значение функции в которой f(Х*)=0.0027.
В результате трех итераций реализации метода крутого восхождения получена точка Х*=[2.056; 1,002]т, значение функции в которой f(Х*)=0.0027.
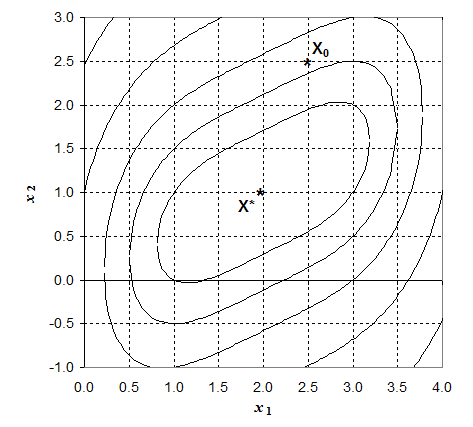 |
Рис.2.8 Траектория поиска минимума функции методом крутого восхождения.
Методы с использованием производных 2-го порядка
