Краткие теоретические сведения. Код, предложенный Варшамовым, является типичным представителем систематических

Код, предложенный Варшамовым, является типичным представителем систематических кодов, т.е. сумма любых разрешенных комбинаций также является разрешенной комбинацией. Благодаря этому возможно построить все комбинации кода, располагая лишь их ограниченным количеством. Построение систематического кода производится на основе образующей матрицы. Образующую матрицу можно представить в виде двух подматриц: информационной |E_k| (единичная матрица, k – количество информационных элементов) и проверочной |C_rk|.

Построение матриц G и Н

Проверочная матрица |C_rk| для кода Варшамова строится подбором различных комбинаций и должна удовлетворять следующим условиям:

1) каждая строка подматрицы |C_rk| должна содержать не менее (d_min - 1) единиц (d_min – минимальное кодовое расстояние);

2) сумма любых j-строк должно иметь не менее (d_min - j) единиц;

3) число столбцов подматрице – r (равно числу проверочных элементов).

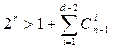, (7)

где n – длина кодовой комбинации.

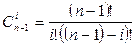. (8)

Код Варшамова, как и любой другой систематический код, способен обнаруживать и исправлять ошибки. Количество исправляемых ошибок:

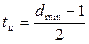, (9)

где t_u – целое число, т.е. в формуле (9) округляется до ближайшего меньшего целого.

Для того чтобы обнаружить, в каком разряде была допущена ошибка, строят проверочную матрицу Н. Проверочная матрица состоит из двух подматриц: |D_kr|, содержащая k столбцов и r строк, и |E_r| – единичная матрица. Каждая строка |D_kr| соответствует столбцу проверочных разрядов подматрицы |C_rk| образующей матрицы G.

Общий вид матриц G и H:

;

;

.

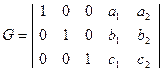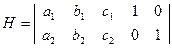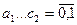Кодирование

Кодовая комбинация, которую необходимо закодировать:

111011111110100111110111.

Допустим, количество исправляемых нашим кодом ошибок:

.

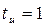Немного преобразовав формулу (9), найдем минимальное кодовое расстояние d_min этого кода:

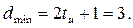
Теперь найдем количество проверочных разрядов r. Для этого воспользуемся следующим неравенством, которое следует из того, что для правильного различия и определения мест ошибок общее число комбинаций проверочных элементов 2^r должно превышать число возможных ошибочных ситуаций в коде, равное 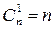, с учетом отсутствия ошибок:

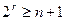. (10)

Учитывая, что n = k + r = 24 + r, преобразуем неравенство:

.

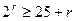Наименьшее натуральное r, удовлетворяющее данному неравенству:

.

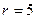Проверим, удовлетворяет ли это значение неравенству (7):

→ → → .

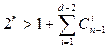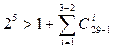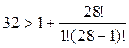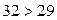Составим порождающую матрицу G, которая будет состоять из двух подматриц: информационной |E₂₄| (единичная матрица, 24 – количество информационных разрядов) и проверочной |C_5,24| (5 – количество проверочных разрядов). Проверочная матрица |C_5,24| будет состоять из 24 строчек 5-разрядных кодовых комбинаций, которые выбираются из всех 32 возможных 5-разрядных комбинаций по следующим критериям:

1) вес кодовых комбинаций должен удовлетворять следующему неравенству:

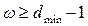, (11)

поскольку d_min = 3, то, следовательно, ;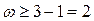

2) кодовое расстояние между комбинациями должно удовлетворять условию:

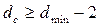, (12)

поскольку d_min = 3, то, следовательно, .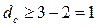

Выписываем все 32 возможные 5-разрядные двоичные кодовые комбинации и подчеркиваем те, которые удовлетворяют обоим условиям:

00000 01000 10000 11000

00001 010011000111001

00010 010101001011010

00011010111001111011

00100 011001010011100

00101011011010111101

00110011101011011110

00111011111011111111

Строим проверочную матрицу из 24 удовлетворяющих условия кодовых комбинаций и составляем порождающую матрицу G из единичной матрицы |E₂₄| и проверочной матрицы |C_5,24|:

Закодированную кодовую комбинацию получаем путем последовательного сложения по модулю 2 соответствующих строк порождающей матрицы G. Строки, участвующие в сложении, выбираются следующим образом: если в кодовой комбинации в разряде, порядок которого соответствует номеру определенной строки порождающей матрицы, стоит 1, то эта строка участвует в сложении. Кодовые комбинации, которые необходимо сложить для получения нашего закодированного сообщения, подчеркнуты. Проделав эту операцию, получим следующую закодированную кодовую комбинацию:

1110 11111110 1001 11110111 10101.

Декодирование

Пускай при передаче закодированного сообщения произошла ошибка в 22-ом разряде, и декодер получил следующую искаженную кодовую комбинацию:

=

1110 11111110 1001 1111 0011 10101.

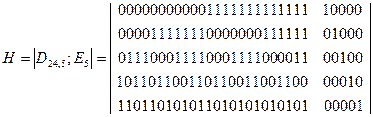
Для того чтобы обнаружить в каком разряде была допущена ошибка, строим проверочную матрицу Н, которая будет состоять из двух подматриц: |D_24,5|, каждая строка которой соответствует столбцу проверочных разрядов подматрицы |C_5,24| образующей матрицы G, и единичной матрицы |E₅|:

По формуле

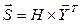(13)

вычисляем синдром ошибки:

.

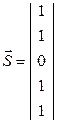Найденный синдром соответствует 22-му столбцу проверочной матрицы Н, следовательно, ошибка произошла в 22-ом разряде полученной кодовой комбинации, то есть этот разряд необходимо инвертировать. В полученной комбинации меняем в 22-ом разряде 0 на 1, отбрасываем проверочные разряды и получаем декодированное сообщение с исправленной ошибкой:

1110 11111110 1001 11110111.

Код Хэмминга