Краткие теоретические сведения. Код Хэмминга – один из наиболее распространенных систематических кодов

Код Хэмминга – один из наиболее распространенных систематических кодов. К кодам Хэмминга относятся коды с минимальным кодовым расстоянием d_min = 3, исправляющие все одиночные ошибки.

Формирование r проверочных элементов в комбинации этого кода осуществляется по k информационным элементам. Таким образом, длина кодовой комбинации n = r + k. Проверочные элементы представляют собой линейные комбинации информационных элементов, т.е. взвешенные суммы информационных элементов с весовыми коэффициентами 1 и 0. Для двоичных кодов в качестве линейной операции используют сложение по модулю 2. Операция вычитания совпадает с операцией сложения.

Последовательность 0 и 1 в кодовой комбинации иначе называют кодовым вектором. Коду Хэмминга присущи свойства линейных кодов:

1) сумма или разность кодовых комбинаций кода дает вектор, принадлежащий данному коду;

2) линейные коды образуют алгебраическую группу по отношению к операции сложения по модулю 2;

3) минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.

При передаче кодового вектора может быть искажен любой элемент, число таких ситуаций равно 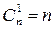. К этому следует добавить еще одну ситуацию, когда ошибка не произошла. Таким образом, общее число комбинаций проверочных элементов 2^r должно превышать число возможных ошибочных ситуаций в коде с учетом отсутствия ошибок для правильного их различия и определения мест ошибок (формула 10):

.

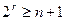Поскольку

,

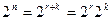то, учитывая формулу (10), можно записать:

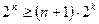(14)

где 2ⁿ – полное число комбинаций кода.

Минимальное соотношение корректирующих и информационных разрядов, ниже которого код не может сохранять свои корректирующие способности, определяется из формулы (10):

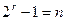. (15)

Для вычисления основных параметров кода Хэмминга можно задать число проверочных элементов r, когда из последнего выражения определяют n и k = n - r. Соотношения между r, n и k для кода Хэмминга приведены в таблице 7:

Таблица 7

Соотношения между r, n и k для кода Хэмминга

r

n

k

Характерной особенностью проверочной матрицы кода с d_min = 3 является то, что ее столбцы представляют собой различные ненулевые комбинации длиной r. Например, при r = 4 и n = 15, код (15, 11), проверочная матрица имеет вид:

H15,11 =

u1

u2

u3

u4

u5

u6

u7

u8

u9

u10

u11

u12

u13

u14

u15

Итак, если взять комбинации простого четырехэлементного кода и отбросить нулевую комбинацию, то можно легко получить проверочную матрицу, записав все кодовые комбинации последовательно в столбцы матрицы H.

Перестановкой столбцов, содержащих одну единицу, вправо матрицу приводим к виду:

H15,11 =

a1

a2

a3

a4

a5

a6

a7

a8

a9

a10

a11

a12

a13

a14

a15

В соответствии с этой матрицей, получаем систему проверочных уравнений, с помощью которой вычисляем проверочные разряды:

b1 =	a5 (+)	a6 (+)	a7 (+)	a8 (+)	a9 (+)	a10 (+)	a11
b2 =	a2 (+)	a3 (+)	a4 (+)	a8 (+)	a9 (+)	a10 (+)	a11
b3 =	a1 (+)	a3 (+)	a4 (+)	a6 (+)	a7 (+)	a10 (+)	a11
b4 =	a1 (+)	a2 (+)	a4 (+)	a5 (+)	a7 (+)	a9 (+)	a11

При появлении ошибки в кодовой комбинации окажутся невыполненными те проверочные отношения, в которые входит значение ошибочного разряда. Так, если ошибка возникла в 7-м информационном разряде, то окажутся невыполненными 1, 3 и 4 уравнения, т.е. синдром равен 1011 (совпадает с 7-м столбцом матрицы H). Таким образом, местоположение столбца матрицы H, совпадающего с вычисленным синдромом, указывает место ошибки. Вычисленное значение синдрома обязательно совпадает с одним из столбцов матрицы H, т.к. в качестве столбцов выбраны все возможные двоичные r-разрядные числа.

Хэмминг предложил расположить столбцы проверочной матрицы так, чтобы номер i-го столбца матрицы H и номер ошибочного разряда кодовой комбинации соответствовали двоичному представлению числа i. Тогда синдром, полученный из проверочных уравнений, будет двоичным представлением номера разряда кодовой комбинации, в котором произошла ошибка. Для этого проверочные разряды должны находиться не в конце кодовой комбинации, а на номерах позиций, которые выражаются степенью двойки (2⁰, 2¹, 2², ... 2^r-1), как это имеет место в непреобразованной матрице H, потому что каждый из них входит только в одно из проверочных уравнений.

В последнем случае проверочные разряды размещаются между информационными. Синдром, согласно непреобразованной проверочной матрице H_15,11, определяется из уравнений:

S1 =	u1	(+) u3	(+) u5	(+) u7	(+) u9	(+) u11	(+) u13	(+) u15
S2 =	u2	(+) u3	(+) u6	(+) u7	(+) u10	(+) u11	(+) u14	(+) u15
S3 =	u4	(+) u5	(+) u6	(+) u7	(+) u12	(+) u13	(+) u14	(+) u15
S4 =	u8	(+) u9	(+) u10	(+) u11	(+) u12	(+) u13	(+) u14	(+) u15

В качестве проверочных выбирают разряды u₁, u₂, u₄ и u₈, которые встречаются в этой системе уравнений по одному разу.

Кодирование

Кодовая комбинация, которую необходимо закодировать (две первых буквы ФИО – МК):

11101111 11101001.

Воспользовавшись неравенством (10):

,

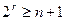найдем количество проверочных разрядов r. Учитывая, что n = k + r = 16 + r, преобразуем неравенство:

.

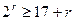Наименьшее натуральное r, удовлетворяющее данному неравенству: r = 5. Следовательно, n = k + r = 16 + 5 = 21.

Зная параметры нашего кода (k = 16, r = 5, n = 21), составляем для него матрицу кода Хэмминга:

H21,16 =

b1

b2

a1

b3

a2

a3

a4

b4

a5

a6

a7

a8

a9

a10

a11

b5

a12

a13

a14

a15

a16

u1

u2

u3

u4

u5

u6

u7

u8

u9

u10

u11

u12

u13

u14

u15

u16

u17

u18

u19

u20

u21

Проверочные столбцы и соответствующие им проверочные символы выделены полужирным шрифтом.

Нужно определить проверочные разряды в комбинации:

u₁ u₂ 1 u₄ 110 u₈ 1111111 u₁₆ 01001.

Из проверочной матрицы получаем:

u1 =	u3	(+) u5	(+) u7	(+) u9	(+) u11	(+) u13	(+) u15	(+) u17	(+) u19	(+) u21
u2 =	u3	(+) u6	(+) u7	(+) u10	(+) u11	(+) u14	(+) u15	(+) u18	(+) u19
u4 =	u5	(+) u6	(+) u7	(+) u12	(+) u13	(+) u14	(+) u15	(+) u20	(+) u21
u8 =	u9	(+) u10	(+) u11	(+) u12	(+) u13	(+) u14	(+) u15
u16 =	u17	(+) u18	(+) u19	(+) u20	(+) u21

Вычисляя проверочные разряды согласно этой системе, для нашей кодовой комбинации получим:

u1 =		(+) 1	(+) 0	(+) 1	(+) 1	(+) 1	(+) 1	(+) 0	(+) 0	(+) 1	= 1
u2 =		(+) 1	(+) 0	(+) 1	(+) 1	(+) 1	(+) 1	(+) 1	(+) 0		= 1
u4 =		(+) 1	(+) 0	(+) 1	(+) 1	(+) 1	(+) 1	(+) 0	(+) 1		= 1
u8 =		(+) 1	(+) 1	(+) 1	(+) 1	(+) 1	(+) 1				= 1
u16 =		(+) 1	(+) 0	(+) 0	(+) 1						= 0

Подставим полученные значения проверочных разрядов и получим закодированное сообщение

111111011111111001001.

Декодирование

Пускай при передаче закодированного сообщения произошла ошибка в 11-ом разряде, и декодер получил следующую искаженную кодовую комбинацию:

111111011101111001001.

Вычислим синдром ошибки. Согласно непреобразованной проверочной матрице H_21,16, синдром определяется из уравнений:

s1 =	u1	(+) u3	(+) u5	(+) u7	(+) u9	(+) u11	(+) u13	(+) u15	(+) u17	(+) u19	(+) u21
s2 =	u2	(+) u3	(+) u6	(+) u7	(+) u10	(+) u11	(+) u14	(+) u15	(+) u18	(+) u19
s3 =	u4	(+) u5	(+) u6	(+) u7	(+) u12	(+) u13	(+) u14	(+) u15	(+) u20	(+) u21
s4 =	u8	(+) u9	(+) u10	(+) u11	(+) u12	(+) u13	(+) u14	(+) u15
s5 =	u16	(+) u17	(+) u18	(+) u19	(+) u20	(+) u21

Вычисляя синдром согласно этой системе, для принятой кодовой комбинации получим:

s1 =

(+) 1

(+) 1

(+) 0

(+) 1

(+) 0

(+) 1

(+) 1

(+) 0

(+) 0

(+) 1

= 1

s2 =

(+) 1

(+) 1

(+) 0

(+) 1

(+) 0

(+) 1

(+) 1

(+) 1

(+) 0

= 1

s3 =

(+) 1

(+) 1

(+) 0

(+) 1

(+) 1

(+) 1

(+) 1

(+) 0

(+) 1

= 0

s4 =

(+) 1

(+) 1

(+) 0

(+) 1

(+) 1

(+) 1

(+) 1

= 1

s5 =

(+) 0

(+) 1

(+) 0

(+) 0

(+) 1

= 0

Очевидно, что для получения правильного результата биты синдрома необходимо записать, начиная со старшего, т.е. s₅s₄s₃s₂s₁. Следовательно, синдром имеет вид:

01011₂ = 11₁₀.

Полученный результат свидетельствует о том, что ошибка допущена в 11-м разряде принятой кодовой комбинации.

Инвертируем искаженный 11-й разряд принятой комбинации, отбрасываем проверочные 1-й, 2-й, 4-й, 8-й и 16-й разряды и получаем декодированное сообщение с исправленной ошибкой:

11101111 11101001.