Краткие теоретические сведения. Коды Бергера относятся к разряду несистематических кодов
Коды Бергера относятся к разряду несистематических кодов. Существует несколько вариантов построения кодов Бергера. В наиболее простом варианте кодирование происходит следующим образом: в информационной части кода подсчитывается число единиц, после чего формируются проверочные разряды, представляющие инвертированную запись этого числа в двоичной форме. Таким образом, число проверочных разрядов R равно наименьшему целому числу, превышающему log2(k), то есть R >= log2(k).
Коды Бергера предназначены для использования в ассиметричных каналах связи, где возможно только либо преобразование нулей в единицы, либо наоборот.
Преимущество кодов Бергера по сравнению с кодами с постоянным весом заключается в том, что они являются разделимыми кодами с очень простым алгоритмом построения проверочной части. В симметричных каналах такие коды обнаруживают все одиночные ошибки и некоторую часть многократных.
Кодирование
Кодовая комбинация, которую необходимо закодировать:
111011111110100111110111.
Количество единиц в слове – 19, в двоичном представлении – 10011. Инвертируем это число – 01100 – и добавляем его к исходному слову. Получаем закодированную кодовую комбинацию:
111011111110100111110111 01100.
Поскольку количество избыточных символов – 5, а длина закодированной кодовой комбинации – 29, то избыточность будет равняться (см. формулу (1)):
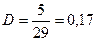 .
.
Декодирование
Декодируем полученную кодовую комбинацию:
111011111110100111110111 01100.
Зная, что количество информационных символов – 24, подсчитываем количество единиц в информационном блоке – их 19. Берем 5 избыточных символов – 01100 – и инвертируем избыточный блок – 10011. Переводим полученное число в десятичный вид – 19. Оно совпадает с количеством единиц в информационном блоке. Это означает, что ошибок, которые мы можем обнаружить, нет. Значит, отбрасываем проверочные символы и получаем декодированное сообщение:
111011111110100111110111.
Код на одно сочетание
Краткие теоретические сведения
Коды на одно сочетание (коды с постоянным весом) характеризуются тем, что их кодовые комбинации содержат одинаковое число единиц, или же, иначе говоря, постоянное отношение количества символов “0” и “1”.
Коды с постоянным весом позволяют обнаружить все ошибки кратности q = 1, ..., n за исключением случаев, когда число единиц, перешедших в нули, равно числу нулей, перешедших в единицы. В полностью асимметричных каналах, в которых имеет место только один вид ошибок (преобразование нулей в единицы или единиц в нули), такой код дозволяет обнаружить все ошибки. В симметричных каналах вероятность необнаруженной ошибки можно определить как вероятность одновременного искажения одной единицы и одного нуля.
Кодирование
Кодовая комбинация, которую необходимо закодировать:
111011111110100111110111.
Закодируем данное сообщение, разделив его на 3 кодовых слова и кодируя каждое отдельно кодом с постоянным весом 8. Следовательно, длина каждого закодированного слова будет составлять 16 символов – 8 информационных и 8 избыточных.
Кодируем каждое слово отдельно, добавляя в конце избыточный блок длиной в 8 символов с таким числом единиц, которое дополняет количество информационных единиц до 8.
1) 1110111110000000, 2) 1110100111100000, 3) 1111011110000000.
Собираем эти три закодированных слова в одно сообщение, и получаем следующую закодированную кодовую комбинацию:
111011111000000011101001111000001111011110000000.
Поскольку количество избыточных символов в каждом закодированном слове – 8, а длина закодированного слова – 16, то избыточность будет равняться (см. формулу (1)):
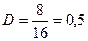 .
.
Декодирование
Декодируем полученную кодовую комбинацию:
111011111000000011101001111000001111011110000000.
Зная, что полученное сообщение состоит из трех отдельно закодированных кодом с постоянным весом 8 слов, декодируем отдельно каждое слово длиной в 16 символов. Поскольку вес всех закодированных кодовых слов равен 8, то ошибок, которые мы можем обнаружить, нет. Зная, что 8 избыточных символов находятся в конце закодированного слова, отбрасываем их и получаем три декодированных слова:
1) 11101111, 2) 11101001, 3) 11110111.
Собираем эти три декодированных слова в одно сообщение, и получаем следующую декодированную кодовую комбинацию:
111011111110100111110111.
