Высшие гармоники напряжения и тока в схемах выпрямителей

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ МАШИНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ АВТОМАТИЗАЦИИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

КАФЕДРА АВТОМАТИКИ И ПРОЦЕССОВ УПРАВЛЕНИЯ

Курсовая работа

по дисциплине «Информационные технологии в электронике»

на тему: «Аппроксимация экспериментально

полученных зависимостей»

Выполнил: Плюшкин Д.И.

студент 4-ого курса

специальность: 2 10105

шифр: 610324

Проверила: Конева Н.Е.

Москва, 2014 г.

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

МАШИНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ АВТОМАТИЗАЦИИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

КАФЕДРА АВТОМАТИКИ И ПРОЦЕССОВ УПРАВЛЕНИЯ

Задание на курсовую работу:

Получить аналитическое описание графиче ски заданных зависимостей в варианте №5 для кривых n=3 и n=6 методом Лагранжа, Ньютона, Форсайта и сравнить точности каждого из методов при решении данной задачи.

Выполнила: Плюшкин Д.В.

студент 4-ого курса

специальность: 210105

шифр: 610324

Проверила: Конева Н.Е.

Москва, 2014 г.

Содерж ание

1. Высшие гармоники напряжения и тока в схемах выпрямителей…………………………………………………….
2. Методы анализа…………………………………………………………..
	2.1 Алгебраический полном Лагранжа………………………………..
		2.1.1. Аппроксимация функций с помощью алгебраических интерполяционных полиномов…………………………………….
		2.1.2 Интерполяционная формула Лагранжа……………………
	2.2 Интерполяционный полином Ньютона…………………………
	2.3 Методы наименьших квадратов Форсайта…………………….
3. Анализ кривых…………………………………………………………….
	3.1 Кривая n=3…………………………………………………………...
		3.1.1 Алгебраический полином Лагранжа для n=3……………….
		3.1.2 Метод наименьших квадратов Форсайта для n=3………
		3.1.3 Интерполяционный полином Ньютона для n=3…………
	3.2 Кривая n=6…………………………………………………………...
		3.2.1 Алгебраический полином Лагранжа для n=6……………….
		3.2.2 Метод наименьших квадратов Форсайта для n=6………
		3.2.3 Интерполяционный полином Ньютона для n=6…………
4. Нахождение погрешностей……………………………………………..
	4.1 Для кривой n=3………………………………………………………
	4.2 Для кривой n=6………………………………………………………
Вывод………………………………………………………………………….
Список литературы………………………………………………………...

Высшие гармоники напряжения и тока в схемах выпрямителей

Кривая выпрямленного напряжения любой схемы выпрям­ления всегда содержит две составляющие: постоянную, равную среднему значению выпрямленного напряжения, и перемен­ную, которая состоит из определенного спектра гармоник. Если рассмотреть наиболее важный для практики режим — рабо ту выпрямителя с большой сглаживающей индуктивностью, то можно заметить, что в этом случае все схемы имеют одинако­вую регулировочную характеристику 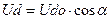и один и тот же предельный угол регулирования 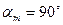. Это позволяет объединить рассмотрение схем и получить формулу, одинаково пригодную для нахождения амплитуд высших гармоник вы­прямленного напряжения для всех рассмотренных ранее схем.

Кривые выпрямленного напряжения рис.1.1 представляют собой периодические функции. Очевидно, подобные функции удовлетворяют условию Дирихле и могут быть разложены в ряд Фурье. Ряд будет содержать постоянную составляющую, первую гармонику, период которой будет равен периоду ис­ходной функции, а также спектр высших гармоник, частоты которых кратны частоте первой гармоники.

В общем виде выпрямленное напряжение 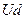может быть записано следующим образом:

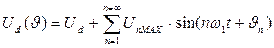, (1.1)

где

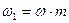- угловая частота первой гармоники;

т - кратность пульсаций в кривой выпрямленного напря­жения;

n - порядок высшей гармоники;

U птах - амплитуда высшей гармоники порядка п;

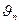- начальная фаза высшей гармоники n-го порядка.

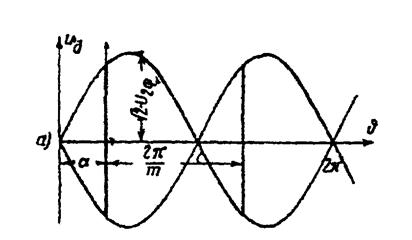
Рис. 1.1 Кривые 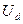для однофазной схемы со средней точкой

Для величин 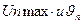могут быть даны следующие вы­ражения:

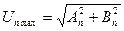, (1.2)

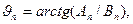(1.3)

где А_n и В_n определяются выражениями:

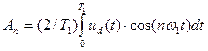, (1.4)

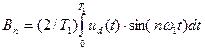, (1.5)

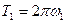- период повторяемости в кривой выпрямленного напряжения.

Кривую 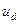в интервале повторяемос ти 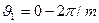для всех схем можно описать следующим уравнением:

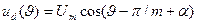, (1.6)

Это соотношение справедливо для любой схемы выпрям­ления, так как момент отпирания очередного вентиля всегда отстоит от нуля синусоиды соответствующего фазного напря­жения на угол .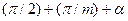

Подставив (1.6) в (1.4) и (1.5) и сделав подстановку 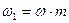, получим:

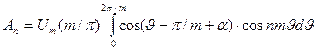, (1.7)

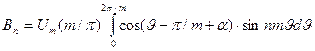, (1.8)

В конечном результате для величины 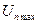может быть получено следующее выражение:

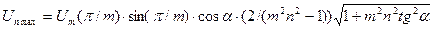, (1.9)

Величина 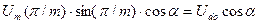, входящая в выражение (1.9), является средним значением выпрямленного напряжения регулируемого выпрямителя .

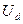Следовательно,

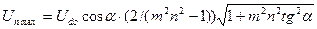, (1.10)

Часто в расчетах используется относительная величина:

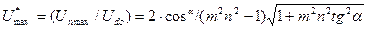, (1.11)

Графики зависимости 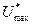для трехфазной схемы со сред­ней точкой (т=3) приведены на рис.1.2.

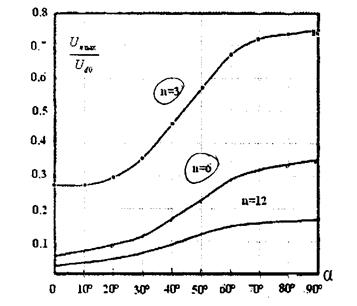
Рис.1.2 Зависимость высших гармоник выпрямленного напряжения от угла регулирования

Методы анализа

Из приведённого выше рисунка для анализа берутся кривые n=3 и n=6. Анализироваться эти кривые будут тремя методами:

1. Алгебраическими полиномами Лагранжа;
2. Интерполяционными полиномами Ньютона;
3. Наименьших квадрато в Форсайта.