Лекция 3. Метрические методы распознавания

Метрические методы связаны с измерением расстояний в пространстве признаков.

Будем характеризовать состояние системы (изделия) вектором параметров

.

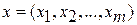Компоненты вектора 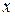могут быть непрерывными или дискретными вели­чинами. В последнем случае 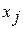представляет собой (многоразрядный) диагностический признак.

Каждое состояние изделия, в соответствии с данным равенством, может быть представлено точкой в пространстве признаков, а вектор 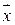соединяет эту точку с началом координат. Предполагается, что точки с одним и тем же состоянием (диагнозом) группируются в компактной области пространства признаков («гипотеза компактности»).

Вопрос 1. Метод эталонов

Допустим, что имеется 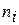образцов с диагнозом 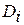(рис.5). Они образуют обучающую последовательность. Точки, входящие в области диагнозов, обычно располагаются более плотно в центральной части области.

Примем в качестве «типичного» изделия с данным диагнозом «среднюю точку», которую назовем эталоном.

Координаты эталона 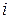-го диагноза

( ),

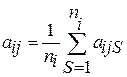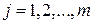где 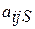– значение параметра 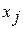для образца 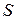, принадлежащего диагнозу .

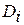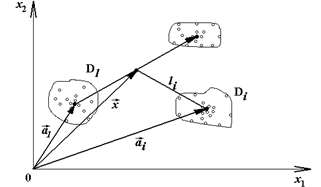
Рис. 5. Область диагнозов (состояний) в пространстве признаков

Пусть предъявлено для распознавания изделие, характеризующееся вектором 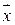в пространстве признаков. Решение вопроса об отнесении изделия к диагнозу 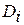связано с измерением расстояния до эталонов.

Решающее правило принимается по минимальному расстоянию до эталона:

, ,

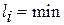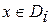т, е. если точка 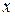ближе всего к эталону диагноза 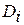, то вывод делается в пользу диагноза .

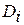Расстояния до i-го эталона

.

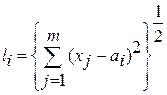Предыдущие равенства определяют обычное евклидово расстояние.

В задачах диагностики часто оказывается целесообразным использовать обобщенные расстояния порядка .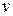

.

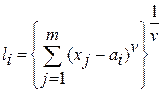При v=1 получается расстояние по Хемингу, при v = 2 – обычное расстояние. При возрастании v увеличивается роль наибольшего отклонения по какой-либо координате.

Расстояние можно использовать для однородного, изотропного прост­ранства признаков. Таким пространством будет пространство простых (двухразрядных) признаков, кодируемых двоичными числами (0,1).

Однако в задачах технической диагностики часто приходится использовать признаки различной физической природы (например, уровень вибрационных перегрузок и повышение температуры), имеющие различную размерность.

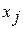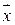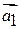Для учета указанного обстоятельства целесообразно ввести безразмерные расстояния. Например, по координате (направлению) для точек и безразмерное расстояние можно принять в виде

,

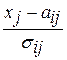где 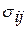– среднее квадратическое отклонение признака 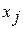для диагноза .

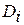Условие содержит предположение, что для диагностики отклонение следует относить к «характерному масштабу» – среднему квадратическому отклонению.

Далее следует учесть различную диагностическую ценность признаков.

Для этого введем безразмерные диагностические коэффициенты 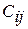и тогда получим

.

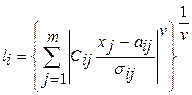Последние соотношения дают формулы для расстоянии в неоднородном, неизотропном пространстве.

Определение коэффициентов 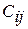вызывает известные трудности. В тех случаях, когда отсутствуют статистические сведения, величины 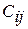можно назначать с помощью экспертных оценок или подбирать по опыту диагностики.

Вопрос 2. Метод минимального расстояния до множества

В этом методе учитывается минимальное расстояние до образцов, входящих в обу­чающую последовательность.

На рис.6 показаны расстояния 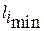и .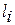

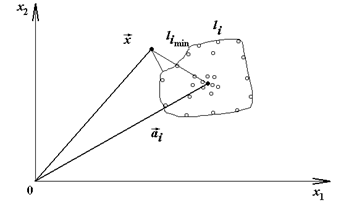
Рис.6. Метод минимального расстояния до множества

Решающее правило имеет вид

, ,

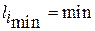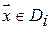т. е. если точка 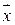ближе всего к одной из точек обучающей последовательности диагноза 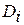, то точка относится к этому диагнозу.

Метод минимального расстояния до множества представляет собой диагностику «по прецеденту», т. е. по образцу (изделию), наиболее близко напоминающему объект, предъявленный для распознавания.

Дополнение к решающему правилу в метрических методах

Метрические методы распознавания, в отличие от вероятностных, основаны на детерминистском подходе. Решающее правило устанавливает диагноз, считая его достоверным.

Обучающая последовательность, как уже указывалось ранее, составляется из образцов (изделий), для которых достоверно известен диагноз.

По смыслу задачи распознавания, если минимальное расстояние до эталона диагноза 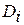мало отличается от других расстоянии, достоверность диагноза 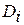вызывает сомнения.

Вводятся условные «вероятности» диагнозов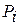

,

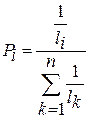где 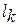– расстояние до эталона диагноза .

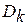Решение в пользу диагноза 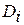принимается в случае, если

,

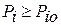где 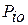– уровень принятия решения для i-го диагноза (обычно ).

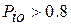Такой способ сближает вероятностные и детерминистские методы распознавания. Применение метрических методов возможно и в том случае, когда области диагнозов пересекаются.

ЛИТЕРАТУРА

1. И.А.Биргер. Техническая диагностика. – М.: Машиностроение, 1978.

2. В.А. Пивоваров. Повреждаемость и диагностирование авиационных конструкций. – М.: Транспорт, 1994

******************************************************************