Способы измерения информации

Ответ на этот вопрос зависит от того, что понимать под информацией

Существуют различные подходы к измерению информации

1. Содержательный подход (вероятностный).

Пусть информация — это знания человека

Т. О. Сообщение информативно (содержит ненулевую информацию), если оно пополняет знания человека

Пример: прогноз погоды на завтра — информативное сообщение

вчерашний прогноз — неинформативное

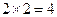— информативно для первоклассника

#define — неинформативно

Единица измерения информации — 1 бит (от англ. Binary digit — двоичная цифра)

Сообщение, уменьшающее неопределённость знаний в 2 раза, несёт в себе 1 бит информации

Неопределённость знаний в некотором событии — это количество возможных результатов события

! Варианты (результаты) должны быть равновероятны — не иметь преимуществ друг перед другом

Пример: бросание монетки (орёл, решка) — неопределённость =2

бросание кубика — неопределённость =6

вытаскивание жребия

Т. О. Сообщение, что произошло одно из двух равновероятных событий несёт в себе 1 бит информации

задача Студент на экзамене может получить одну из 4-х оценок: 5,4,3,2. Пусть результат экзамена равновероятный. На вопрос: «Что получил?», студент ответил: «4». Сколько бит информации содержится в его ответе?

Сразу ответить сложно

Будем отгадывать оценку, задавая вопросы, на которые можно ответить только «да» или «нет» (вопросы будем задавать так, чтобы каждый ответ уменьшал количество вариантов в 2 раза 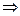1 бит информации)

1. Оценка выше 3? ДА

число вариантов уменьшилось в 2 раза (осталось только 4 или 5) 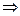1 бит

2. Ты получил 5? НЕТ — 1 бит

Т. О. Сообщение о том, что произошло одно из 4-х равновероятных событий несёт 2 бита информации

задача На книжном стеллаже 8 полок. Книга может быть поставлена на любую из них. Сколько бит информации содержит сообщение о том, где лежит книга?

1. Книга лежит выше 4-ой полки? НЕТ

2. Книга лежит ниже 3-ей полки? ДА 3 бита

3. Книга лежит на 2-ой полке? НЕТ

! Если сразу сказано, что книга лежит на 1-ой полке из 8, то это сообщение тоже несёт 3 бита информации

Получим общую формулу:

Обозначим

i – количество информации, сообщение о том, что произошло одно из N событий (исходов);

N – количество исходов (неопределённость знаний)

задание Определите N и i в примерах

с монетой N=2 i=1

с оценками N=4 i=2

со стеллажами N=8 i=3

Формула Хартли (1928 г.) 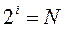— показательное уравнение

Проверим, полученные ранее результаты:

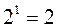
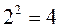
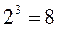
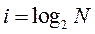Обычно i — неизвестно, N — известно

задание Сколько информации мы получим после того, как бросим кубик?

N=6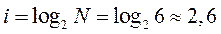

2. Алфавитный подход

Множество, используемых в языке символов, наз. алфавитом

цифры, (, знаки препинания, пробел (промежутки между словами), тоже включаются в алфавит

Полное число символов алфавита наз. мощностью алфавита N

Пример: мощность алфавита из русских букв и дополнительных символов равна 54

Пусть текст поступает последовательно по одному знаку (например, бумажная лента, выползающая из телеграфного аппарата)

Пусть каждый появляющийся символ с одинаковой вероятностью может быть любым символом алфавита

(на самом деле не так)

В алфавите N символов, каждый символ несёт i бит информации:

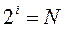
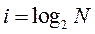
Для N=54 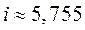бит

Пример: страницы книги содержат 50 строк, в каждой строке 60 символов, т.о. страница несёт в себе 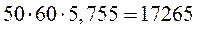бит

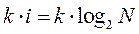
i –информационный вес одного символа алфавита;

k – количество символов

Т.О. количество информации не зависит от содержания нельзя сравнить по объёму книги на разных языках (т.к. разные мощности алфавитов)

Является объективным способом измерения информации

Удобен в использовании технических средств работы с информацией