Лекция 6. Фрактальная графика

Фракталы встречаются везде, где заканчиваются правильные формы евклидовой геометрии. Все, что создано человеком, ограничено плоскостями. Если встречается природный объект, то с первого взгляда видно, что осознать, описать его форму со всеми шероховатостями можно только приблизительно. Здесь на помощь приходят фракталы.

Определение фрактала, данное Мандельбротом, звучит так:

"Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому"

Одним из основных свойств фракталов является самоподобие.

В самом простом случае небольшая часть фрактала содержит информацию обо всем фрактале.

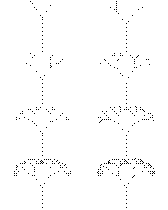Рис. 77

Фрактал — это объект, отдельные элементы которого наследуют свойства родительских структур.

Самыми известными фрактальными объектами являются деревья: от каждой ветки ответвляются меньшие, похожие на нее, от тех — еще меньшие и так далее.

Фрактальными свойствами обладают многие природные объекты: снежинка при увеличении оказывается фракталом; по фрактальным алгоритмам растут кристаллы и растения. Если посмотреть на береговую линию моря на картах все более крупного масштаба, то становятся видны все новые изгибы и изломы, похожие на более крупные.

Появление новых элементов меньшего масштаба происходит по простому алгоритму. Очевидно, что описать такой объект можно всего лишь несколькими математическими уравнениями!

По отдельной ветке математическими методами можно проследить свойства всего дерева.

n Отображением называется операция, ставящая в соответствие каждому элементу одного множества элемент другого множества. Например, отображение x → x2 ставит в соответствие числу 2 из множества действительных чисел число 4 из того же множества; числу 3 - число 9 и т. д.

n Мнимая единица (i) — число, квадрат которого равен –1.

n Комплексное число — число вида a + b•i, где a и b — действительные числа.

n Комплексная плоскость — плоскость, на которой введена декартова система координат, в которой по оси абсцисс откладывается параметр a, по оси ординат — параметр b. Каждая точка комплексной плоскости представляет собой определенное комплексное число.

Алгоритм построения фрактала

1. Выбираем точку на комплексной плоскости.
2. Действуем на нее отображением x → x2 + С, в результате чего точка «перемещается» на плоскости.
3. На полученную точку повторно действуем отображением, и так несколько раз (несколько итераций).
4. Если в результате этого точка «убегает» на бесконечность — красим ее в белый цвет, если «прыгает» вокруг своего исходного положения — в черный.
5. Повторяем описанные действия для всех точек плоскости.

Классификация фракталов по виду

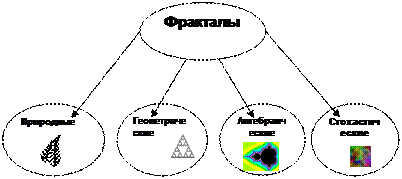Рис. 78

Природные фракталы

Очевидные примеры – дерево, куст, колония кораллов. Еще более наглядным примером может служить соцветие «сложный зонтик» – «зонтик», состоящий, в свою очередь, из маленьких зонтиков.

Одним из известнейших природных фракталов является «Папоротник» (рис. 75). Приведем алгоритм создания этого фрактала.

Рис. 79. Фрактал «Папоротник»

Строится этот фрактал по следующему алгоритму.

program fern;

usescrt,graph;

Var

gd,gm:integer;

proceduredraw;

Const

iterations=50000;

Var

t ,x,y,p:real;

к:longint;

mid_x,mid_y,radius:integer;

Begin

mid_x:=getmaxX div2;

mid_y:=getmaxY;

radius:=trunc(0.l*mid_y);

randomize;

x:=l.0;

y:=0.0;

fork:=l toiterations do begin

p:=random;

t:=x;

ifp<=0.85 then begin

x:=0.85 * x + 0.04 * y;

y:=-0.04 * t + 0.85 * у + 1.6

end elseif p<=0.92 then begin

x:=0.2 * x - 0.26 * y;

y:=0.23 * t + 0.22 * у + 1.6

end elseif p<=0.99 then begin

x:=-0.15 * x + 0.28 * у;

y:=0.26 * t + 0.24 * у + 0.44

End else begin

x:=0.0;

y: =0. 16 * у

end;

putpixel(midx+round(radius*x),mid_y-round(radius*y), light green)

End

end;

Begin

gd:=detect;

initgraph(gd,gm,'c:\bp\bgi');

draw;

readkey;

closegraph

End.

Одним из приложений теории фракталов является генерация фрактальных деревьев. Следующая программа генерирует фрактальное дерево весьма похожее на реальное. Программа написана на языке Pascal.

Строится ствол дерева случайной длины, от него строятся несколько ветвей тоже случайной длины, при этом толщина уменьшается, далее от каждой ветки строится еще несколько веток, и цикл повторяется. При этом на каждом шаге проверяется длина ветки, если она меньше некоторой заранее определенной величины, то вместо веток рисуется лист, и для этой ветки процесс прекращается. При этом можно изменять самые разные параметры, от ветвистости, толщины ствола и веток, до угла наклона веток и цвета листьев (рис. 76).

Рис. 80. Фрактальные деревья

programFracTree;

uses Graph, CRT;

procedureTree(x, y: Integer; a: Real; 1: Integer);

Var

xl, yl : Integer;

p, s : Integer;

i : Integer;

al : Real;

Begin

if 1<8 thenexit;

xl := Round(x + l*cos(a));

yl := Round(y + l*sin(a));

if1 > 100 thenp:=100 else p:=l;

if p < 40 then begin

{Генерация листьев}

ifRandom > 0.5 thenSetColor(lO) elseSetColor(2); {4, 14}

fori:=0 To3 doLine(x+i, y, xl, yl)

End

Else begin

{Генерация веток}

SetColor (6) ;

fori:=0 to(p div6) doLine(x+i-(p div12), y, xl, yl);

end;

{Следующие ветки}

fori:=0 to9-Random(9) do begin

s := Random(l-l div 6) + (1 div 6);

al:= a + 1.6*(0.5-Random); {Угол наклона веток}

xl:= Round(x + s*cos(a));

yl:= Round(y + s*sin(a));

Tree(xl, yl, al, p-5-Random(30)); {Чем меньше вычитаем,

тем пышнее дерево}

end;

end;