Геометрические фракталы. Именно с них началась история фракталов

Именно с них началась история фракталов. Это и есть те функции-монстры, которых так называли за не дифференцируемость в каждой точке. Геометрические фракталы являются также самыми наглядными, т.к. сразу видна самоподобность. Вообще все геометрические фракталы обладают т.н. жесткой самоподобностью, не изменяющейся при изменении масштаба. Для построения геометрических фракталов характерно задание "основы" и "фрагмента", повторяющегося при каждом уменьшении масштаба. Поэтому эти фракталы иногда называют конструктивными или автомодельными.

Примерами таких фракталов являются Треугольник Серпинского, Снежинка Коха, Кривая Коха, Кривые Леви и Минковского и многие другие. В графике геометрические фракталы применяются для получения изображений деревьев, кустов, береговых линий и т.д.

Построение триадной кривой Коха

1. Построение кривой начинается с единичного отрезка, который называется инициатором и является предфракталом 0-го порядка.

2. Далее инициатор заменяется на образующий элемент - кривую из четырех прямолинейных звеньев, каждое из которых имеет длину 1/3. Так образуется предфрактал 1-го порядка. Его длина равна 4/3.

3. Для построения предфрактала следующего порядка каждое звено заменяется на уменьшенный образующий элемент.

4. В результате получаем кривую, состоящую из 4 x 4 = 16 звеньев, каждое из которых имеет длину (1/3) / 3 = 1/9, общая длина равна 16/9. Длина предфрактала n-го порядка равна (4/3) в степени n.

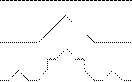Рис.81. Кривая Коха

Очевидно, что предел длины кривой при n, стремящийся к бесконечности, равен бесконечности. В итоге получили кривую бесконечной длины, заполняющую ограниченное множество на плоскости, что само по себе очень любопытно.

Следующая программа реализует данный метод.

programKoh;

uses CRT, Graph;

Var

gd,gm : Integer;

Const

iter = 50000;

proceduredraw;

Var

t, x, у, р : Real;

к : Longlnt;

mx, my, rad : Integer;

Begin

mx := 10;

my := 250;

rad :=600;

Randomize;

x := 0.0;

у := 0.0;

forк := 1 To iter do begin

p := Random;

t := x;

ifp <= 1/2 then begin

x := 1/2 * x + 1/(2*sqrt(3)) * y;

у := 1/(2*sqrt(3)) * t - 1/2 * y;

End

Else

Begin

x := 1/2 * x - l/(2*sqrt(3)) * у +1/2;

у := -l/(2*sqrt(3)) * t - 1/2 * у + 1/(2*sqrt(3))

end;

PutPixeKmx + Round(rad * x) , my - Round(rad * y) , 2);

end;

end;

Begin

gd := Detect;

InitGraph(gd,gm,'');

draw; ReadKey;

CloseGraph;

End.

Если построение кривой начинать не с отрезка, а с треугольника, и применить вышеперечисленные построения к каждой его стороне, то получим «снежинку» Коха.

Рис. 82. Снежинка Коха

Существуют два основных способа построения геометрических фракталов.

Первый способ - использование L-систем (от имени Lindenmayer), второй способ - применение системы IFS (iterated function systems).

L-система - это грамматика некоторого языка, которая описывает инициатор и преобразование, выполняемое над ним, при помощи средств, аналогичных средствам языка Лого (аксиоматическое описание простейших геометрических фигур и допустимых преобразований на плоскости и в пространстве).

L – системы (рис.77)

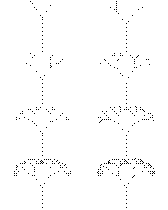Рис. 83

Подобные L-системы применяются в пакете Autodesk 3D Studio для описания цветов и других растений.

Системы итерирующих функций (IFS)

Система итерирующих функций - это совокупность сжимающих аффинных преобразований.

Рис. 84

Рассмотрим подробнее построение кривой Кох с использованием аффинных преобразований. Каждый новый элемент кривой содержит четыре звена, полученных из образующего элемента использованием масштабирования, поворота и переноса.

1. Для получения первого звена достаточно сжать исходный отрезок в три раза. Следует отметить, что то же масштабирование применяется для всех звеньев.
2. Следующее звено строится с использованием всех возможных преобразований, а именно: сжатие в три раза, поворот на - 60^о и параллельный перенос на 1/3 по оси X.
3. Третье звено строится аналогично второму: сжатие в три раза, поворот на 60^о, параллельный перенос на 2/3 по оси X.
4. Последнее звено: сжатие в три раза, параллельный перенос на 2/3 по оси X.

Теперь мы можем найти систему итерирующих функций для описания кривой Коха. Осталось только произвести суперпозицию аффинных преобразований - масштабирования, поворота и параллельного переноса.

Из курса линейной алгебры известна формула вычисления новых координат x',y' при аффинных преобразованиях:

x` = x * а - y * b + e

y` = x * c + y * d + f

Здесь

a = cos (alpha) * scale_x,

b = sin (alpha) * scale_x,

c = sin (alpha) * scale_y,

d = cos (alpha) * scale_y,

e = move_x,

f = move_y,

где

scale_x - масштабирование по оси X;

scale_y - масштабирование по оси Y;

alpha - угол поворота;

move_x - параллельный перенос по оси X;

move_y - параллельный перенос по оси Y.

Полученные коэффициенты a, b, c, d, e, f для каждого звена и составят требуемую систему итерирующих функций.

Вычислим коэффициенты аффинного преобразования IFS для кривой Коха.

1. 1. Для первого звена коэффициенты аффинного преобразования будут следующими: a = 0.3333, b = 0.0000, c = 0.0000, d = 0.3333, e = 0.0000, f = 0.0000.

Полученное аффинное преобразование является масштабированием на коэффициент 1/3=0,3333.

2. Вычислим коэффициенты преобразования для второго звена: a = 0.1667, b = -0.2887, c = 0.2887, d = 0.1667, e = 0.3333, f = 0.0000.

3. Коэффициенты для третьего звена будут такими:
a = -0.1667, b = 0.2887, c = 0.2887, d = 0.1667, e = 0.6666, f = 0.

4. 4. И наконец, коэффициенты преобразования для последнего звена: a = 0.3333, b = 0.0000, c = 0.0000, d = 0.3333, e = 0.6666, f = 0.0000.

Коэффициенты для первого и последнего звеньев кривой Коха практически идентичны и отличаются только параллельным переносом по оси X (коэффициент e).

Второе и третье преобразования включают в себя не только масштабирование и перенос, но и поворот на 60о и -60о.

Здесь коэффициенты вычисляются так:

0.1667 = cos (60) * 1/3,

-0.2887 = -sin (60) * 1/3

Значение последнего (седьмого) параметра каждого преобразования пропорционально площади, занимаемой звеном.

Сумма последних параметров для всех преобразований равна единице.

В нашем примере размеры звеньев равны, поэтому седьмой параметр равен 1/4=0.25 для всех звеньев

В том случае, если оценить приблизительно размеры не удается, можно использовать формулу вычисления площади p = abs (a * d - b * c). Следует учитывать то, что эта формула дает не нормализованный результат. Поэтому нам придется еще приводить сумму к единице.

Проверить формулу можно на нашем примере, используя коэффициенты, задающие кривую Кох в формате IFS для программы FRACTINT:

1: 0.3333 * 0.3333 - 0.0000 * 0.0000 = 0.111

2: 0.3333 * 0.3333 - 0.0000 * 0.0000 = 0.111

3: 0.1667 * 0.1667 + 0.2887 * 0.2887 = 0.111

4: -0.1667 * 0.1667 - 0.2887 * 0.2887 = 0.111

Теперь подбором нормирующего множителя можно нормализовать значение седьмого параметра до значения 0.25. Седьмой параметр применяется при построении фрактала с использованием IFS. Если для построения фрактала используем систему итерирующих функций, получаем изображение, деталировка которого ограничена только разрешением устройства отображения, в отличие от построения, основанного на L-системе, где точность зависит от заданного порядка предфрактала.

Чтобы получить высокое разрешение с использованием L-систем, необходимо задавать большой порядок предфрактала. Но так как построение основано на рекурсивном алгоритме, соответственно получается большая глубина рекурсии и, как следствие, замедление построения.