Экспертные оценки и способы измерений

Оценки экспертов — это количественные или качественные измерения соот­ветствующих показателей.

В зависимости от целей экспертизы эксперты могут оценивать стоимость недвижимости, ожидаемый уровень инфляции, изменения валютного курса, надежность эми­тента ценной бумаги, рейтинг банка и т.д. Объекты оценки и оцениваемые показатели весьма разнообразны. Если при этом эксперт должен измерить значение коли­чественного показателя (дать количественную оценку), он может указать конкретное числовое значение или ин­тервал, в котором оно лежит.

Методы получения количественных экспертных оценок

· Непосредственная количественная оценка. Эксперт непосредственно указывает числовое значение по­казателя для оцениваемого объекта (альтерна­тивы), например, стоимость квартиры или зе­мельного участка, предполагаемую емкость рынка и т.п. Если конкретное значение показателя ука­зать трудно, эксперт может определить диапазон, в котором находится это значение.

· Метод средней точки. Этот метод используется, когда альтернативных вариантов, требующих оценки, достаточно много. В начале эксперт ко­личественно оценивает наиболее предпочтитель­ную альтернативу — f(a1) и наименее предпочти­тельную – f(a2). Далее он должен подобрать тре­тий альтернативный вариант a3, оценка которого f(a3) расположена в середине между значениями f(a1) и f(a2) и равна половине их суммы. Затем экспертом определяется оценка альтернативы a4, значение которой — f(a4) — расположено посере­дине между значениями f(a1) и f(a3) и альтерна­тивы a5 — f(a5). значение которой является сред­ним значением между f(a3) и f(a2), и так далеедотех пор, пока не будет дана оценка всех сравни­ваемых альтернатив.

Методы получения качественных экспертных оценок

Основные понятия о структурировании множества альтернатив

Рассмотрим основные типы структур. Первый из них называется КЛАССИФИКАЦИЯ.

Рассмотрим рис.5.

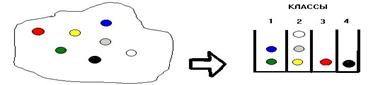
Рис.5. Пример классификации

Слева изображено неструктурированное множество альтернатив. Справа показано разбиение исходного множества на 4 класса. Можно считать, что каждый класс есть подмножество исходного множества альтернатив. Здесь важно отметить, что классы НЕУПОРЯДОЧЕНЫ друг относительно друга. Т.е. нельзя сказать, что какой-то класс "важнее (лучше, старше, дороже и п.т.)" другого. Например, людей можно классифицировать по полу или национальности. Правильная постановка диагноза - также пример классификации. Компьютерные системы, помогающие врачу ставить диагноз, существуют. И решают они именно задачу классификации, т.е. отнесения больного к нужному классу, который эквивалентен названию болезни. (А как же быть с легкими и тяжелыми заболеваниями? Ведь по определению классы НЕ упорядочены. Действительно, заболевания можно упорядочивать по тяжести, но здесь мы договоримся не принимать это в расчет.)

Второй способ структурирования называется СТРАТИФИКАЦИЯ. Это название произошло от английского термина "страта", (strata) что означает "слой", "пласт". Иными словами, стратификация есть разбиение множества на ряд уровней или слоев. В отличие от классов, страты упорядочены. Рассмотрим рисунок

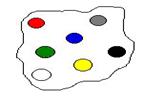
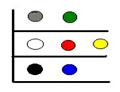
Рис.6. Пример стратификации

Серая и зеленая альтернативы помещены на верхнюю страту. Это означает, что они одинаковы по значимости (для ЛПР) и, одновременно, важнее (лучше) остальных альтернатив. В примере с обменом квартиры, если удалось стратифицировать варианты, то окончательный выбор, естественно, будет сделан среди вариантов, занимающих верхнюю страту. Удобно считать, что страты выражают некоторые уровни "качества". Несколько примеров классических стратификаций:

· оценки уровня знаний ("отлично", "хорошо" и т.д.)

· звезды отелей

· спортивные разряды

Связь страт с неким абстрактным "качеством" крайне важна для понимания идеи стратификации. Пятизвездный отель не просто лучше двухзвездного, а можно говорить на сколько он лучше.

Следующий способ структурирования называется РАНЖИРОВАНИЕ. Внешне он напоминает стратификацию (см. предыдущий рисунок), но в отличие от нее уровни НЕ выражают "качества", а трактуются просто как "номер в списке". Это различие настолько важно, что на нем стоит остановиться подробнее. Упорядочение называется ранжировкой, если указан только номер места объекта в упорядочении (и больше ничего). Если нам сообщают только места, полученные спортсменами по результатам соревнований (но не сообщают результаты), то это - типичная ранжировка. Например, объявляют, что первые 3 места распределились следующим образом:

1. Иванов

2. Петров

3. Сидоров

Если указанные спортсмены - прыгуны в высоту, то, зная результаты каждого, можно было бы говорить на сколько, к примеру, Иванов прыгнул выше Петрова или Сидорова. Знание только мест (без результатов) дает нам право говорить, что Иванов лучше Петрова, но не дает нам возможности говорить "на сколько лучше". Места в ранжировке естественно называются "рангами". Ранг 1 принято присваивать наилучшему объекту. (Вспомним морское "капитан 1-го ранга"). Итак, в отличие от стратификации, здесь играет роль только номер "полочки", на которую кладут альтернативы. Один и тот же ранг может быть присвоен нескольким объектам. Тогда ранжировка называется нестрогой. Тогда как в строгой ранжировке каждому объекту присваивается уникальный номер ранга. В терминах спортивного примера, нестрогая ранжировка - это когда Петров и Сидоров делят второе место.

Мы рассмотрели в общих чертах основные понятия структуризации множества альтернатив. Вспомним теперь, что структура была нам нужна не сама по себе, а с целью выполнить ВЫБОР. Классификация здесь стоит особняком, поскольку для нее выбор сводится по сути к выбору определенного класса, к которому следует отнести альтернативу. Стратификация и ранжировка предоставляют нам более широкие возможности выбора.

Но как выполнить структуризацию? Как найти структуру в изначально аморфном множестве альтернатив? Этим мы теперь и займемся. Методы структуризации - это по существу и есть сердцевина поддержки принятия решений.