Избыточность информации

Если бы сообщения передавались с помощью равновероятных букв алфавита и между собой статистически независимых, то энтропия таких сообщений была бы максимальной. На самом деле реальные сообщения строятся из не равновероятных букв алфавита с наличием статистических связей между буквами. Поэтому энтропия реальных сообщений -H_р, оказывается много меньше оптимальных сообщений - H_о. Допустим, нужно передать сообщение, содержащее количество информации, равное I. Источнику, обладающему энтропией на букву, равной H_р, придется затратить некоторое число n_р, то есть

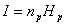
Если энтропия источника была бы Н₀, то пришлось бы затратить меньше букв на передачу этого же количества информации

I= n₀H₀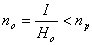

Таким образом, часть букв n_р-n_о являются как бы лишними, избыточными. Мера удлинения реальных сообщений по сравнению с оптимально закодированными и представляет собой избыточность D.

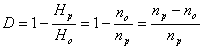(3)

Но наличие избыточности нельзя рассматривать как признак несовершенства источника сообщений. Наличие избыточности способствует повышению помехоустойчивости сообщений. Высокая избыточность естественных языков обеспечивает надежное общение между людьми.

Частотные характеристики текстовых сообщений

Важными характеристиками текста являются повторяемость букв, пар букв (биграмм) и вообще m-ок (m-грамм), сочетаемость букв друг с другом, чередование гласных и согласных и некоторые другие. Замечательно, что эти характеристики являются достаточно устойчивыми.

Идея состоит в подсчете чисел вхождений каждой n^m возможных m-грамм в достаточно длинных открытых текстах T=t₁t₂…t_l, составленных из букв алфавита {a₁, a₂, ..., a_n}. При этом просматриваются подряд идущие m-граммы текста

t₁t₂...t_m, t₂t₃... t_m+1, ..., t_i-m+1t_l-m+2...t_l.

Если 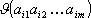– число появлений m-граммы a_i1a_i2...a_im в тексте T, а L общее число подсчитанных m-грамм, то опыт показывает, что при достаточно больших L частоты

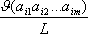для данной m-граммы мало отличаются друг от друга.

В силу этого, относительную частоту считают приближением вероятности P (a_i1a_i2...a_im) появления данной m-граммы в случайно выбранном месте текста (такой подход принят при статистическом определении вероятности).

Для русского языка частоты (в порядке убывания) знаков алфавита, в котором отождествлены E c Ё, Ь с Ъ, а также имеется знак пробела (-) между словами, приведены в таблице 1.

Таблица 1

- 0.175	О 0.090	Е, Ё 0.072	А 0.062
И 0.062	Т 0.053	Н 0.053	С 0.045
Р 0.040	В 0.038	Л 0.035	К 0.028
М 0.026	Д 0.025	П 0.023	У 0.021
Я 0.018	Ы 0.016	З 0.016	Ь, Ъ 0.014
Б 0.014	Г 0.013	Ч 0.012	Й 0.010
Х 0.009	Ж 0.007	Ю 0.006	Ш 0.006
Ц 0.004	Щ 0.003	Э 0.003	Ф 0.002

Некоторая разница значений частот в приводимых в различных источниках таблицах объясняется тем, что частоты существенно зависят не только от длины текста, но и от его характера.

Устойчивыми являются также частотные характеристики биграмм, триграмм и четырехграмм осмысленных текстов.