Действия над множествами
Объединением множеств A и B называется множество элементов, принадлежащих по крайней мере одному из данных множеств (т. е. либо A, либо B, либо одновременно и A и B). Обозначают 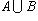 и читают "объединение A и B".
и читают "объединение A и B".
Пересечением множеств A и B называется множество элементов, принадлежащих одновременно и A и B. Обозначают 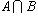 и читают "пересечение A и B".
и читают "пересечение A и B".
Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A\B и читают "разность A и B".
Операции объединения и пересечения множеств обладают многими свойствами сложения и умножения чисел, например переместительным, сочетательным и распределительным свойствами.
Понятия объединения и пересечения множеств дословно переносятся на случай более двух множеств и даже на случай любого конечного или бесконечного множества множеств.
Для удобства будем называть системами такие множества, элементами которых служат другие множества. Тогда объединением множеств некоторой системы называется множество, состоящее из элементов, принадлежащих по крайней мере одному множеству данной системы. Пересечением множеств некоторой системы называется множество, состоящее из элементов, входящих во все множества данной системы.
Применяются следующие обозначения. В случае конечной системы множеств A1, A2, ..., An объединение S и пересечение D обозначаются:
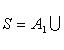
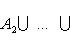
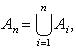
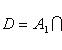
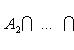
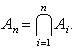
Основные свойства операций над множествами.
Операции объединения и пересечения над множествами обладают рядом свойств. Мы рассмотрим основные, наиболее важные свойства этих операций.
ТЕОРЕМА 1.3. Для любых множеств А, В и С имеем:
1. идемпотентность объединения;
2. идемпотентность пересечения;
3. коммутативность объединения;
4. коммутативность пересечения,
5. ассоциативность объединения,
6. ассоциативность пересечения,
7. дистрибутивность объединения относительно пересечения,
8. дистрибутивность пересечения относительно объединения.
Графы
Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными.
Если ребра ориентированы, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.
Если ребра не имеют ориентации, граф называется неориентированным.
На рис. 17.5. 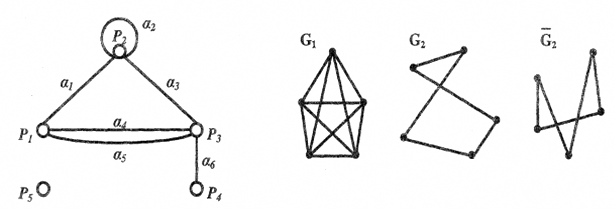 слева изображен граф, имеющий пять вершин и шесть ребер. Если рассматривается множество упорядоченных пар точек, т.е. на каждом ребре задается направление, то граф G называется ориентированным
слева изображен граф, имеющий пять вершин и шесть ребер. Если рассматривается множество упорядоченных пар точек, т.е. на каждом ребре задается направление, то граф G называется ориентированным  . В противном случае G называется неориентированным графом
. В противном случае G называется неориентированным графом  .
.
Степенью вершины называется число ребер, которым принадлежит вершина.
Методы теории графов позволяют найти кратчайший путь между двумя вершинами, способы обхода вершин без возврата и т.п.
Закономерность 1. Число нечетных вершин любого графа четно.
Закономерность 2. Невозможно начертить граф с нечетным числом нечетных вершин.
Закономерность 3. Если все вершины графа четные, то можно начертить этот граф, не отрывая карандаш от бумаги, («одним росчерком»), проводя по каждому ребру только один раз. Движение можно начать с любой вершины и закончить его в той же вершине.
Закономерность 4. Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.
Закономерность 5. Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
С помощью графов часто упрощается решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло- и электросети, маршрутизация в сети. Помогают графы в решении математических и экономических задач.
Рассмотрим пример. Для расследования преступления нужно провести ряд экспертиз. Причем для некоторых экспертиз необходимы результаты других. В какой последовательности следует выполнять работу для наиболее быстрого достижения результата? Для решения этой задачи применяется ориентированный граф, вершинами которого будут экспертизы, а ребра — зависимости одних от результатов других.
