Определение точности оценок показателей надежности

Министерство сельского хозяйства РФ

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Ярославская государственная сельскохозяйственная академия

Кафедра «Технический сервис»

Методические указания

для выполнения контрольной работы по дисциплинам «Надежность технических систем» и «Надежность и ремонт машин» для студентов заочной формы обучения специальностей

110304.65 «Технология обслуживания и ремонта машин в АПК» и

110301.65 «Механизация сельского хозяйства»

Определение точности оценок показателей надежности

Ярославль

Рукописный вариант

Содержание

	Общие сведения
1.1	Требования к опытной информации о надежности машин
	Рекомендации для самостоятельной работы
2.1	Вопросы для самостоятельного изучения
2.2	Литература
	Методические указания по выполнению контрольной работы
3.1	Задание контрольной работы
3.2	Последовательность решения задачи
3.2.1	Составление сводной таблицы исходной информации в порядке возрастания показателей надежности
3.2.2	Статический ряд информации
3.2.3	Определение среднего значения и среднеквадратического отклонения показателей надежности
3.2.4	Проверка информации на выпадающие точки
3.2.5	Графическое изображения опытного распределения
3.2.6	Определение коэффициента вариации
3.2.7	Выбор теоретического закона распределения
3.2.8	Критерии согласия опытных и теоретических распределений показателей надежности
3.2.9	Определение доверительных границ рассеивания одиночного и среднего значений показателя надежности. Абсолютная и относительная предельные ошибки
	Правила оформления контрольной работы
Приложение А ­
Приложение Б
Приложение В
Приложение Г
Приложение Д
Приложение Е
Приложение Ж
Приложение И
Приложение К
Приложение Л – Образец оформления титульного листа

1 Общие сведения

1.1 Требования к опытной информации о надежности машин

Сбор и обработку информации о надежности объектов выполняют с целью усовершенствования конструкции, технологии изготовления, сборки и испытаний объектов, обеспечивающих повышение надежности; разработки мероприятий по совершенствованию диагностирования, технического обслуживания и текущих ремонтов; повышения качества капитальных ремонтов и снижения затрат на их проведение; оптимизации норм расхода запасных частей.

Основные задачи сбора и обработки информации о надежности машин:

- определение показателей надежности объектов;

- выявление конструктивных и технологических недостатков объектов, приводящих к снижению их надежности;

- выявление деталей и сборочных единиц, лимитирующих надежность машины в целом;

- изучение закономерностей возникновения неисправностей и отказов;

- установление влияния условий и режимов эксплуатации на надежность объекта;

- корректировка нормируемых показателей надежности,

- определение эффективности мероприятий по повышению надежности объектов.

В ходе разработки конструкции информация о надежности объектов поступает из лабораторий, проводящих стендовые испытания опытных образцов, а также с заводов, полигонов, машиноиспытательных станций, хозяйств, где машины проходят опытную эксплуатацию.

Информация о надежности объекта должна быть:

- достоверной (истинной, правильной, отражающей объективные факторы без домыслов и догадок);

- полной (исчерпывающей, содержащей все существенные сведения, которые учитывают во время принятия решений);

- однородной (относящейся к одинаковым объектам, эксплуатирующимся примерно в одинаковых условиях);

- дискретной (разделенной по отдельным признакам);,

- своевременной (чтобы могла использоваться для изменения конструкций, корректировки технологического процесса изготовления, ремонта машины и технического обслуживания).

Сбор, обработка и анализ информации о надежности объектов связаны с необходимостью исследования случайных событий и величин. Все показатели надежности сельскохозяйственной техники относят к категории случайных величин, которые рассчитывают методами теории вероятностей и математической статистики.

Статистическую оценку показателей надежности дают совокупности объектов, объединенных единым признаком или свойством. Например, детали можно группировать в совокупности по различным признакам: размерам, отклонениям формы, износам; машины — по долговечности и т. д. Различают статистическую, генеральную и выборочную совокупности.

Статистическая совокупность — это совокупность, состоящая из однородных объектов, обладающих качественной общностью.

Генеральная совокупность - это совокупность всех объектов, подлежащих исследованию. Однако исследовать все объекты генеральной совокупности обычно не представляется возможным. Поэтому для исследования из генеральной совокупности выбирают определенное число объектов, которое называют выборочной совокупностью или выборкой.

Выборочная совокупность (выборка) — определенное число объектов, отобранных из генеральной совокупности для получения объективных сведений о генеральной совокупности.

Для объективной оценки генеральной совокупности очень важен объем выборки, т. е. число объектов наблюдений, составляющих выборку.

Выборка должна быть подобна генеральной совокупности, чтобы на основании ее можно было достаточно уверенно судить об интересующем признаке генеральной совокупности.

Выборка должна быть представительной, каждый объект — отобран случайно и все объекты — иметь одинаковую вероятность попасть в выборку.

Если во время испытаний у каждого объекта выборочной совокупности будет зафиксирован интересующий исследователя показатель надежности, то полученную таким образом информацию называют полной.

Если же испытания ограничивают по времени или наработке объектов и за это время или наработку не у всех объектов выборочной совокупности зафиксирован показатель надежности, то такую информацию называют усеченной.

При этом возможны также случаи преждевременного снятия с испытаний объектов, у которых не зафиксирован показатель надежности и время или наработка которых не достигли заранее оговоренных условиями испытаний значений. Досрочное снятие машин с испытаний возможно при хозяйственной необходимости, авариях, пожарах и других непредвиденных обстоятельствах. Полученную по такой методике испытаний информацию называют многократно усеченной, а преждевременно снятые с испытаний машины - приостановленными.

2 Рекомендации для самостоятельной работы

2.1 Вопросы для самостоятельного изучения

Для освоения материала для решения задачи необходимо дополнительно изучить следующие вопросы по учебникам:

- понятия точечных и интервальных оценок показателей надёжности;

- понятие доверительной границы и доверительной вероятности;

- нижние и верхние доверительные границы;

- влияние вида закона распределения на величины доверительных границ;

- порядок определения доверительных границ;

- абсолютная и относительная ошибка показателей надёжности.

2.2 Литература

1. Технология ремонта машин [Текст] / Под ред. Е.А. Пучина. – М.: КолосС, 2007. - 488с.

2. Практикум по ремонту сельскохозяйственных машин [Текст] / Под ред. В.Е. Рогова. – М.: КолосС, 2007. - 336с.

3. Бодров, В.А. Послеэксплуатационная дефектация деталей. Исследование технического состояния ремонтного фонда МТП [Текст]: Методические указания к лабораторным работам для студентов специальности «Механизация сельского хозяйства» / В.А. Бодров, В.П. Цаплин, В.Ф. Ершова. - Ярославль: ЯГСХА, 2006. - 36 с.

4. Техническое обслуживание и ремонт машин в сельском хозяйстве [Текст] / Под ред. В.И. Черноиванова. - 2-е изд. – М.: Челябинск.: ГОСНИТИ, ЧГАУ, 2003. - 992с.

5. Черноиванов, В.И. Организация и технология восстановления деталей машин [Текст] / В.И. Черноиванов, В.П. Лялякин. - М.: ГОСНИТИ, 2003, - 488c.

6. Методические указания к лаб. работам по курсу: «Основы организации производственного процесса и проектирование ремонтно-обслуживающих предприятий» [Текст]. – Ярославль.: ЯГСХА, 2002. - 30с.

7. Система критериев качества, надежности, экономической эффективности сельскохозяйственной техники [Текст] / Под ред. А.Т. Табашникова. - М.: ФГНУ «Росинформагротех», 2010, - 188c.

8. Черноиванов, В.И. Восстановление деталей машин (Состояние и перспективы) [Текст] / В.И. Черноиванов, И.Г.Голубев. – М.: ФГНУ «Росинформагротех», 2010. - 376с.

9. Шишмарев, В.Ю. Надежность технических систем [Текст]: Учебник для студентов высших учебных заведений / В.Ю. Шишмарев. - М.: Издательский центр «Академия», 2010. - 304с.

10. Малкин, В.С. Надежность технических систем и техногенный риск [Текст]: Учеб. пособ. для студ. ВУЗов, обучающихся по направ. 280100 «Безопасность жизнедеятельности» / В.С. Малкин. - Ростов-на-Дону: Феникс, 2010. - 432с.: ил.

11. Яхьяев, Н.Я. Основы теории надежности и диагностика: Учебник для студентов вузов, обучающихся по специальности «Автомобили и автомобильное хозяйство» направления подготовки «Эксплуатация наземного транспорта и транспортного оборудования» [Текст] / Н.Я. Яхьяев, А.В. Кораблин. - М.: Издательский центр «Академия», 2009. - 256с.

12. Практикум по ремонту машин [Текст]: Учеб. пособие. / Е.А. Пучин, В.С. Новиков, Н.А. Очковский; Под ред. Е.А. Пучина. - М.: КолосС, 2009. - 327с.

13. Нуйкин, А.А. Эксплуатация и ремонт двигателей внутреннего сгорания. Технический справочник [Текст] / А.А. Нуйкин, П.А. Власов, А.М. Галкин. – Пенза: ПензаАГРОТЕХсервис, 2006. - 200c.

3 Методические указания по выполнению контрольной работы

3.1 Задание контрольной работы

а) Ответы на вопросы

Для подготовки ответа на теоретический вопрос студент обязан прочитать соответствующий материал в литературных источниках. Четко уяснить смысл поставленного вопроса. Ответ должен быть конкретным и вместе с этим полностью раскрывать существо вопроса. Ответ на вопрос должен быть пояснен примерами и иллюстрирован схемами. К контрольной работе приложить презентацию подготовленного материала.

б) Решение задачи

Выполнить обработку первичной информации по индивидуальному заданию.

3.2 Последовательность решения задачи

При решении задачи необходимо:

- составить сводную таблицу исходной информации в порядке возрастания показателей надежности (вариационный ряд);

- составить статистический ряд;

- определить среднее значение ( 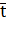) и среднее квадратическое отклонение (σ) показателя надежности;

- проверить информацию на выпадающие точки;

- графически изобразить опытную информацию (построить гистограмму, полигон и кривую накопленных опытных вероятностей показателя надежности);

- определить коэффициент вариации (υ), характеризующий относительное рассеивание показателя надежности;

- выбрать теоретический закон распределения, определить его параметры и графически построить дифференциальную и интегральную кривые;

- оценить совпадения опытного и теоретического распределений по критериям согласия;

- определить доверительные границы одиночных и средних значений показателя надежности и наибольшие возможные ошибки расчета.

3.2.1 Составление сводной таблицы исходной информации в порядке возрастания показателей надежности

Таблица 1.1 – Размеры толщины шлиц первичного вала коробки перемены передач трактора МТЗ-50

№ П/П	Размер, мм	№ П/П	Размер, мм	№ П/П	Размер, мм
	6.01		6.41		6.64
	6.09		6.45		6.67
	6.16		6.46		6.69
	6.22		6.47		6.71
	6.24		6.54		6.73
	6.27		6.56		6.75
	6.28		6.58		6.79
	6.32		6.60		6.81
	6.36		6.61		6.84
	6.39		6.63		6.96

3.2.2 Статический ряд информации

Статистический ряд информации составляется для упрощения дальнейших расчетов в том случае, если повторность исходной информации N не менее 25.

Для построения статистического ряда вся информация разбивается на n интервалов. Ориентировочно количество интервалов определяется по формуле:

где n – число интервалов; N – число исследуемых объектов.

Наиболее рациональное количество интервалов, применяемое на практике n=6…14.

Все интервалы должны быть одинаковыми по величине, прилегать друг к другу и не иметь разрывов.

Для нашего случая:

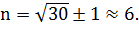
Ширина интервала «А» ориентировочно определяется по формуле:

где t_max – максимальное значение случайной величины;

t_min – минимальное значение случайной величины и округляется до удобной величины.

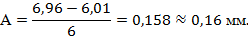
Начало первого интервала принимаем t_1Н=6,0 мм.

Статистический ряд представляет из себя таблицу из четырех строк (таблица 1.2). В первой строке указываются границы интервалов, во второй – количество случаев попадания случайной величины в каждом интервале (частота) m_i , в третьей – опытная вероятность p_i случайной величины, в четвертой – накопленная опытная вероятность .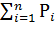

Опытная вероятность определяется как отношение числа случаев m_i к общему объему информации N. Так, например, опытная вероятность в первом и втором интервалах равна:

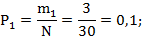
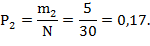
Правильность построения статистического ряда может быть проверена по накопленной вероятности.

Для последнего интервала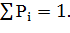

Таблица 1.2 – Статистический ряд информации

Интервал	6,00-6,16	6,16-6,32	6,32-6,48	6,48-6,64	6,64-6,80	6,80-6,96
Частота mi
Опытная вероятность Pi	0,1	0,17	0,2	0,23	0,2	0,1
Накопленная опытная вероятность ∑Pi	0,1	0,27	0,47	0,7	0,9
Середина интервала	6,08	6,24	6,40	6,56	6,72	6,88

3.2.3 Определение среднего значения и среднеквадратического отклонения показателей надежности

Среднее значение является важнейшей характеристикой показателя надежности. На основании средних значений производится планирование работы машины, определение объемов ремонтных работ, составление заявок на запасные части и т.д.

Точность определения среднего значения возрастает по мере увеличения повторности информации, приближаясь к своему пределу – математическому ожиданию.

При наличии статистического ряда среднее значение показателя надежности 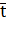определяется по уравнению:

где n – количество интервалов в статистическом ряду;

t_i – значение середины i-го интервала;

Р_i – опытная вероятность i-го интервала.

Средний размер толщины шлиц первичного вала коробки передач, определенный по уравнению 1.3 с использованием статистического ряда будет равен:

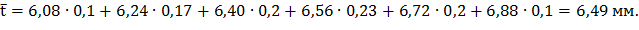
Среднеквадратичное отклонение s является абсолютной характеристикой рассеивания показателя надежности, позволяющей переходить от общей совокупности к показателям надежности отдельных машин. При наличии статистического ряда информации среднее квадратическое отклонение определяется по уравнению:

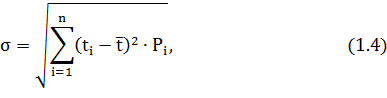
Среднеквадратическое отклонение размера толщины шлиц первичного вала коробки передач, определенного по уравнению 1.4, равно:

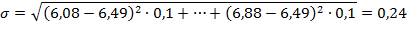
3.2.4 Проверка информации на выпадающие точки

Опытная информация по показателям надежности, полученная в процессе наблюдения за машинами в условиях рядовой эксплуатации, может иметь ошибочные точки, выпадающие из общего закона распределения. Причиной появления выпадающих точек могут быть грубые ошибки в измерениях, ошибочные записи и т.д.

Поэтому, перед окончательной математической обработкой, информация должна быть проверена на выпадающие точки. Проверке обычно подвергаются первые и последние точки.

Первый способ проверки информации на выпадающие точки заключается в проверке по правилу ±3σ. Так как, при законе нормального распределения 99,7% всех точек находятся в интервале 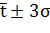, то все точки, входящие в этот интервал, считаются действительными.

Для рассматриваемого примера границы достоверности точек информации будут соответственно равны:

- нижняя граница: 6,49 – 3∙ 0,24 = 5,77;

- верхняя граница: 6,49 + 3∙ 0,24 = 7,21.

Наименьший размер толщины шлиц первичного вала t₁=6,01 мм, что больше 5,77 мм, следовательно, первая точка информации достоверна и должна учитываться при дальнейших расчетах.

Наибольший размер толщины шлиц первичного вала t₃₀=6,96 мм, что меньше 7,21 мм, следовательно, последняя точка информации достоверна и должна учитываться при дальнейших расчетах.

Второй способ проверки достоверности точек производится по критерию l (критерий Ирвина). Этот способ является более точным. При этом определяется опытное значение критерия l_оп по формуле:

где t_i+1, t_i – смежные точки информации, и сравниваются с нормированным значением l.

Если λ_оп < λ точка достоверна; λ_оп > λ точка недостоверна.

Проведя проверку крайних точек информации по доремонтным ресурсам толщины зуба третьей передачи, получим:

для наименьшей точки информации (t = 6,01 мм):

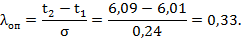
для наибольшей точки информации (t = 6,96):

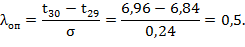
Для объема информации N=30 и доверительной вероятности α=0,95 нормированное значение критерия λ=1,2 (приложение А).

Сравнение опытных значений критерия Ирвина с нормированным его значением показывает, что первая точка информации t = 6,01 мм является достоверной, λ_оп =0,33 < λ=1,2 и её следует учитывать в дальнейших расчетах. Последняя точка информации t₃₀ = 6,96 также является достоверной, λ_оп =0,5 < λ=1,2 и её тоже следует учитывать в дальнейших расчетах.

В случаях, когда исключаются выпадающие точки, нужно перестроить статистический ряд и пересчитать среднее значение и среднее квадратическое отклонение показателя надежности.

3.2.5 Графическое изображения опытного распределения

По данным статистического ряда могут быть построены гистограмма, полигон и кривая накопленных опытных вероятностей (рисунки 1.1, 1.2 и 1.3), которые дают наглядное представление об опытном распределении показателя надежности.

При выборе масштаба при построении графиков желательно придерживаться правила «золотого сечения», т.е.

где y – максимальное значение ординаты;

x – максимальное значение абсциссы.

При построении гистограммы по оси абсцисс откладывают в определенном масштабе показатель надежности t, а по оси ординат - опытную частоту m_i или опытную вероятность P_i.

При построении полигона распределения по оси абсцисс откладывают в определенном масштабе показатель надежности t, а по оси ординат - опытную частоту m_i или опытную вероятность P_i.

Для построения кривой накопленных опытных вероятностей по оси абсцисс откладывают в масштабе значения показателя надежности t, а по оси ординат – накопленную опытную вероятность ∑ P_i.

Точки полигона образуются пересечением ординаты, равной опытной вероятности интервала, и абсциссы, равной середине этого интервала. Точки кривой накопленных опытных вероятностей образуются пересечением ординаты, равной сумме опытных вероятностей и абсциссы - конца данного интервала.

Полигон дает наглядное представление о распределении показателя надежности. Кривая накопленных опытных вероятностей в этом отношении менее наглядна, но с её помощью удобно решать некоторые инженерные задачи.

Гистограмма, полигон и кривая накопленных опытных вероятностей представлены на рисунке 1.1, 1.2 и 1.3.

Pi

ti, мм

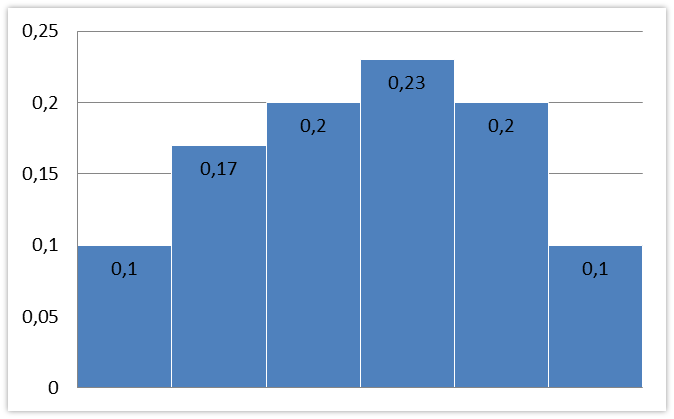
6,00 6,16 6,32 6,48 6,64 6,80 6,96

Рисунок 1.1 – Гистограмма

Pi

ti, мм

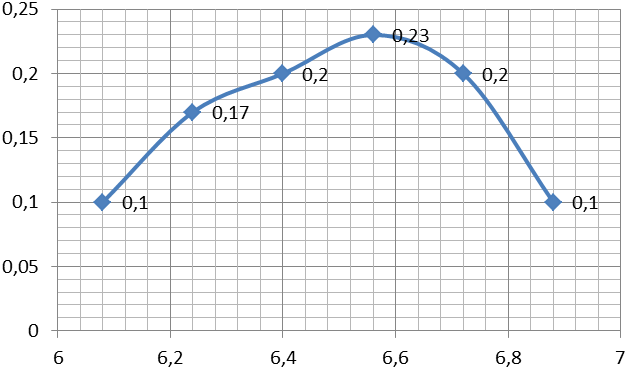
Рисунок 1.2 – Полигон распределения ресурсов

ti, мм

∑Pi

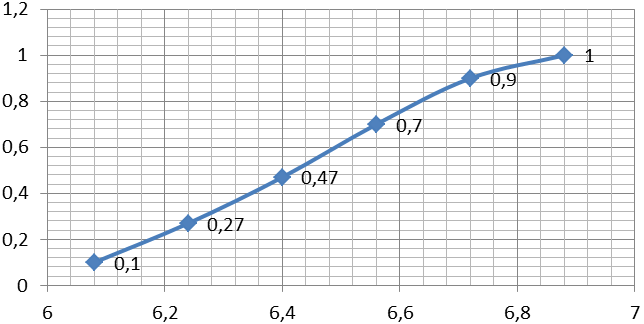
Рисунок 1.3 – Кривая накопленных вероятностей

3.2.6 Определение коэффициента вариации

Коэффициент вариации – это относительная характеристика случайной величины, используется при выборе теоретического закона распределения. Коэффициент вариации V равен отношению σ к среднему значению показателя надежности :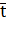

Определение коэффициента вариации по уравнению 1.7 выполняется для тех показателей надежности, зона рассеивания которых начинается от их нулевого значения или близка к нему.

При наличии смещения начала зоны рассеивания t_см величина коэффициента вариации определяется по уравнению:

Учет смешения особенно необходим тогда, когда для выравнивания опытной информации используется теоретический закон распределения Вейбулла, параметры которого непосредственно зависят от величины коэффициента вариации.

Величину смещения t_см, с достаточной для практических расчетов точностью при наличии статистического ряда можно определить:

При отсутствии статистического ряда за смещение принимается величина:

где t₁, t₂, t₃ – значения первого, второго и третьего показателей надежности в порядке возрастания.

Для нашего случая величина смещения равна:

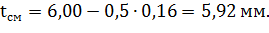
Тогда коэффициент вариации, определенный по формуле 1.8 будет равен:

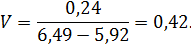
3.2.7 Выбор теоретического закона распределения

Теоретический закон распределения (ТЗР) выражает общий характер изменения показателя надежности и исключает частные отклонения, связанные с недостатком первичной информации, т.е. ТЗР характеризует генеральную совокупность. Опытное распределение имеет частные особенности, которые должны быть исключены при переносе характеристик опытного распределения на генеральную совокупность.

Процесс замены опытных закономерностей теоретическими называется выравнивание опытной информации.

Каждый ТЗР характеризуется двумя функциями:

- f(t) – дифференциальная функция;

- F(t) – интегральная функция.

Применительно к показателям надежности машин, эксплуатируемых в сельском хозяйстве, в подавляющем большинстве случаев используется закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ).

Выбор теоретического закона производится исходя из следующих признаков:

1. По величине коэффициента вариации:

- если V < 0,3 – выбирается ЗНР;

- если 0,3 < V < 0,5 – выбирается ЗНР или ЗРВ;

- если V > 0,5 – выбирается ЗРВ.

2. По области применения.

а) ЗНР применяется, как правило при определении характеристик рассеивания:

- ресурсов и сроков службы машин и агрегатов;

- времени и стоимости восстановления работоспособности машин;

- наработка на ресурсный отказ;

- ошибок измерений размеров деталей.

б) ЗРВ применяется, как правило, при определении:

- ресурсов и сроков службы отдельных деталей и сопряжений;

- доремонтных и межремонтных ресурсов тех элементов машин, отказы которых вызваны выходом из строя одной и той же детали;

- информации по износам деталей.

Здесь применим закон нормального распределения и закон распределения Вейбулла.

Закон нормального распределения (ЗНР)

Отличительной особенностью ЗНР является симметричное рассеивание частных значений относительного среднего.

Дифференциальная функция нормального распределения имеет вид:

где е – основание натурального логарифма, е = 2,718;

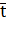–среднее значение показателя надежности;

σ – среднее квадратическое отклонение;

π = 3,14;

t – текущее значение показателя надежности.

Интегральное функция или функция распределения F(t) определяется интегрированием функции плотности вероятностей f(t) и имеет вид:

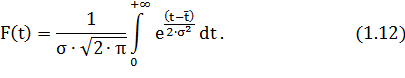
Обе эти функции имеют два параметра: 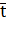– параметр масштаба и σ – параметр формы. Эти параметры определяются на основании опытной информации. Найденные параметры можно подставить в уравнения 1.11 и 1.12 и использовать ими, но это довольно сложная задача.

Если в уравнении 1.11 значение 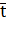приравнять к нулю, σ к единице, то получим центрированную и нормированную дифференциальную функцию:

Из уравнений 1.11 и 1.13 соотношение между f(t) и f₀(t) имеет вид:

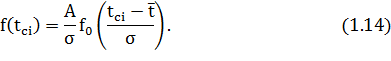
Значение дифференциальной функции 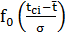находится в приложении Б.

Из уравнения 1.13 также следует, что:

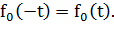
Центрированная и нормированная интегральная функция (t = 0; σ = 1) определяется по уравнению:

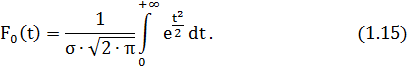
Из уравнений 1.12 и 1.15 получим:

где t_ki – значение конца i-го интервала статистического ряда.

Из уравнения 1.15 следует:

Значение интегральной функции 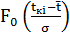находится в приложении В.

При обработке опытной информации установлено:

- средний ресурс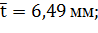

- среднее квадратическое отклонение σ = 0,24 мм;

- коэффициент вариации V = 0,42.

Для построения дифференциальной кривой f(t) определяется теоретическая вероятность попадания случайной величины в каждом интервале статистического ряда (таблица 1.2).

Так, вероятность того, что деталь потребует ремонта в первом и втором интервале наработок будет равна:

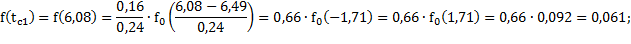
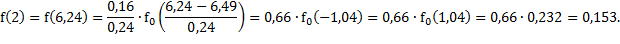
Результаты расчетов представлены в таблице 1.3.

Для построения интегральной кривой определяются значения функции F(t) для концов интервалов статистического ряда.

Для первого интервала получим:

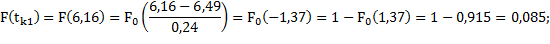
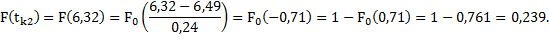
Дальнейшие результаты расчетов представлены в таблице 1.3.

Таблица 1.3 – Значения f(t) и F(t) при ЗНР

Интервалы, мм	6,00-6,16	6,16-6,32	6,32-6,48	6,48-6,64	6,64-6,80	6,80-6,96
f(t)	0,061	0,153	0,245	0,243	0,166	0,071
F(t)	0,085	0,239	0,484	0,732	0,902	0,975

Графики дифференциальной и интегральной функций для закона нормального распределения представлены на рисунке 1.4 и 1.5.

ti, мм

f(t)

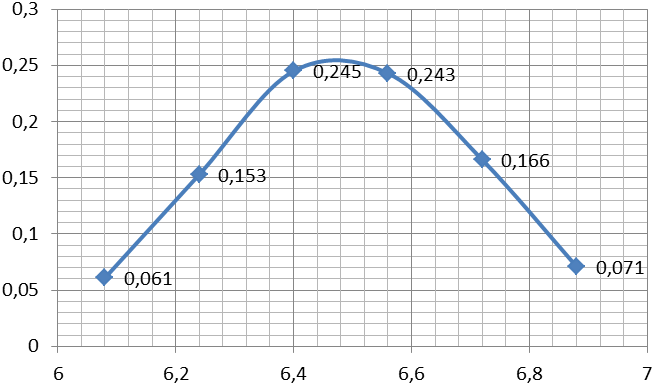
Рисунок 1.4 – График дифференциальной функции

F(t)

ti, мм

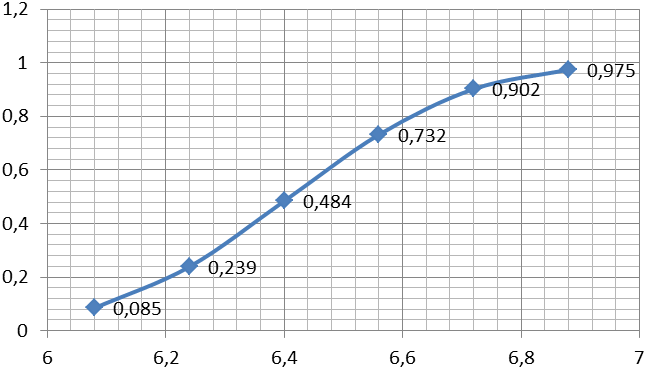
Рисунок 1.4 – График интегральной функции

Закон распределения Вейбулла (ЗРВ)

Отличительной особенностью закона распределения Вейбулла является правосторонняя асимметрия дифференциальной функции.

Дифференциальная f(t) и интегральная F(t) функции определяются уравнениями:

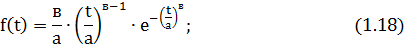
где а и в – параметры распределения Вейбулла.

Определение параметров "а" и "в" аналитическим путем довольно трудоемко, поэтому на практике при их определении пользуются специальными таблицами.

Порядок определения дифференциальной и интегральной функций при ЗРВ следующий:

1. Определение, на основании опытной информации, среднего значения случайной величины 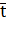, среднего квадратического отклонения σ и коэффициента вариации.

2. По таблицам по известному значению коэффициента вариации V определяются параметр "в" и коэффициенты Вейбулла К_в и С_в .

3. Параметр "а" определяется из выражения:

или

Из приложения Г по известному коэффициенту вариации V получим: в=2,5; К_в=0,887; С_в=0,380.

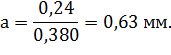
4. Зная параметры "а" и "в" и пользуясь табулированными функциями аf(t) и F(t), можно определить дифференциальную и интегральную функции.

При нахождении функции f(t) для каждого интервала статистического ряда определяется отношение 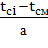, где t_ci – середина i-го интервала. По найденному отношению при определенной величине параметра "в" по приложению Д определяем значение функции аf(t_ci-t_см), нормированной по "а".

Значение функции f(t) для i-го интервала статистического ряда определится из выражения:

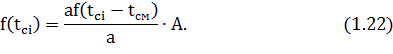
Для нахождения функции F(t) для каждого интервала определяется отношение 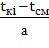, где t_кi – конец i-го интервала. По найденному отношению и параметру "в" по приложению Е определяем значение интегральной функции F(t_кi – t_см).

Для данного задания значение дифференциальной и интегральной функций при ЗРВ будут равны:

для первого интервала:

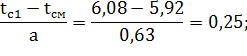
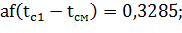
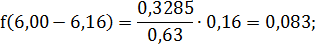
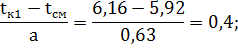
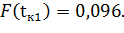
для второго интервала:

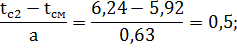
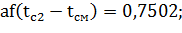
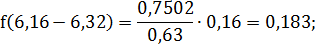
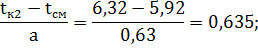
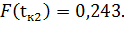
Дальнейшие результаты расчетов представлены в таблице 1.4.

Таблица 1.4 – Значения f(t) и F(t) при ЗРВ

Интервалы, мм	6,00-6,16	6,16-6,32	6,32-6,48	6,48-6,64	6,64-6,80	6,80-6,96
f(t)	0,083	0,183	0,247	0,234	0,15	0,069
F(t)	0,096	0,243	0,536	0,719	0,902	0,969

Графическое изображение дифференциальной функции f(t) и интегральной функции F(t) при выравнивании по ЗРВ представлено на рисунке 1.5 и 1.6.

ti, мм

f(t)

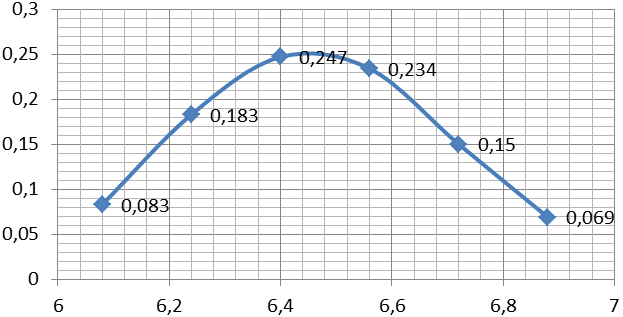
Рисунок 1.5 – График дифференциальной функции

F(t)

ti, мм

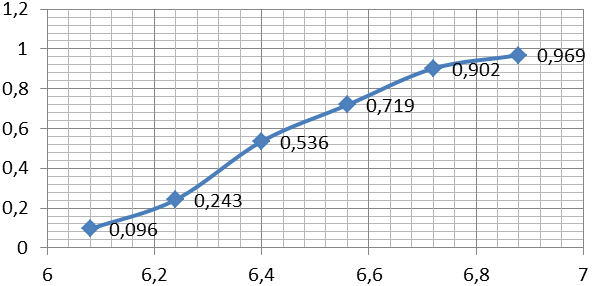
Рисунок 1.6 – График интегральной функции

3.2.8 Критерии согласия опытных и теоретических распределений показателей надежности

Применительно к показателям надежности тракторов и сельскохозяйственных машин, чаще используется критерий согласия Пирсона χ².

Критерий χ² определяется по формуле:

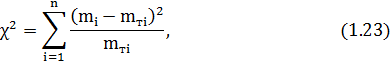
где n – число интервалов в статистическом ряду;

m_i – опытная частота в i-ом интервале;