Метод последовательного преобразования
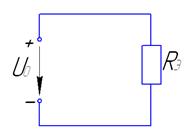
Этот метод заключается в том, что разветвленная электрическая схема сводится к простейшей. Определяется общий неизвестный ток, а затем, возвращаясь последовательно к изначальной схеме, определяются остальные неизвестные токи и падения напряжений.
Последовательное соединение сопротивлений
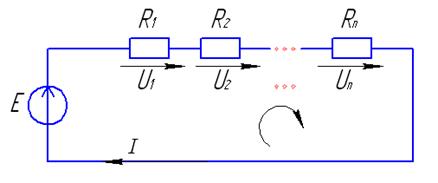
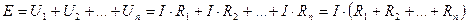
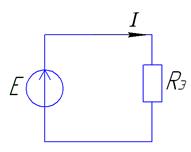
Введем эквивалентное сопротивление
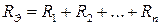
Вывод: при последовательном соединении элементов их сопротивления суммируются ( 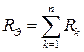 ).
).
Параллельное соединение сопротивлений
Параллельное соединение – это такое соединение, при котором элементы заключены между двумя одними и теми же узлами.
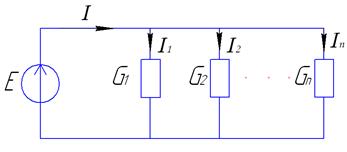
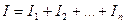
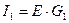 , где
, где 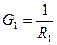
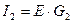 , где
, где 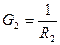
…
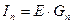 , где
, где 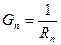
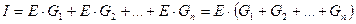
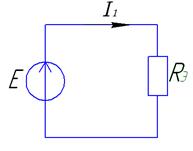
Введем эквивалентную проводимость 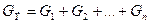 ,
,
тогда 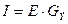
Вывод: при параллельном соединении элементов их проводимости суммируются ( 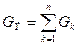 ).
).
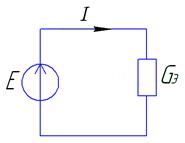
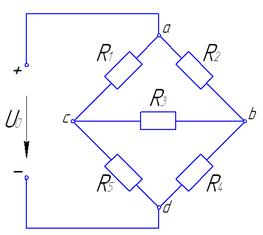
Пример:
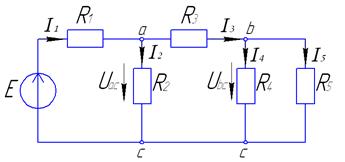
0)
 Известны э.д.с.,
Известны э.д.с., 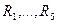 . Определить токи во всех ветвях и падения напряжения на всех элементах методом преобразования.
. Определить токи во всех ветвях и падения напряжения на всех элементах методом преобразования.
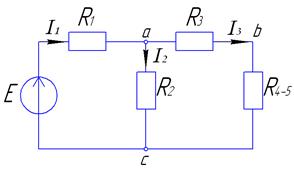
1)
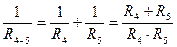
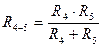
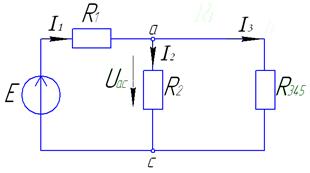 2)
2)
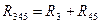
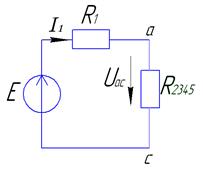
3) 4)
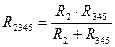
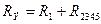
Из схемы 4) можно определить:
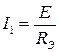
Из схемы 3) можно определить:
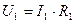 ;
; 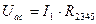
Из схемы 2) можно определить:
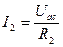 ;
; 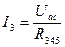
Из схемы 1) можно определить:
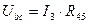 ;
; 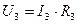
Из схемы 0) можно определить:
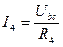 ;
; 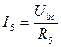
Кроме параллельного и последовательного соединения, существуют соединения «Звезда» и «Треугольник»
Переход от схемы «Звезда» к схеме «Треугольник»
 |
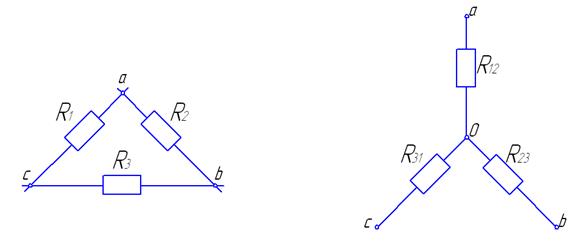
Известны 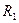 ,
, 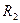 ,
, 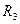 . Определить
. Определить 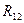 ,
, 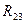 ,
, 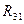 .
.
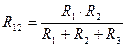
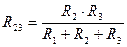
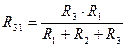
Переход от схемы «Треугольник» к схеме «Звезда»
 |
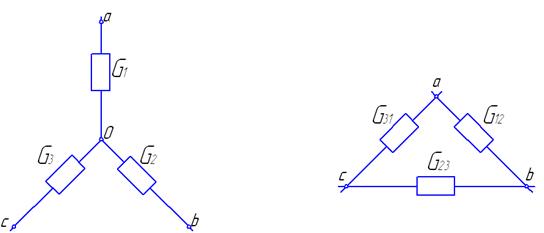
Известны 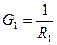 ,
, 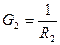 ,
, 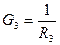 . Определить
. Определить 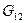 ,
, 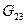 ,
, 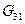 .
.
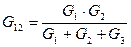
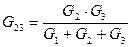
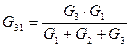
 Пример:
Пример:
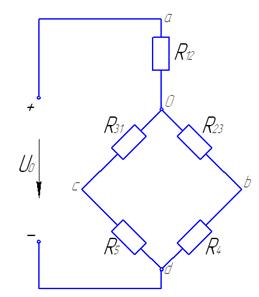
0) 1)
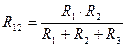 ;
; 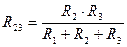 ;
; 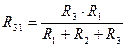
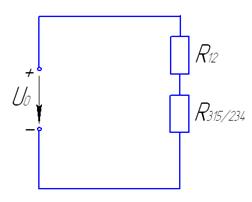
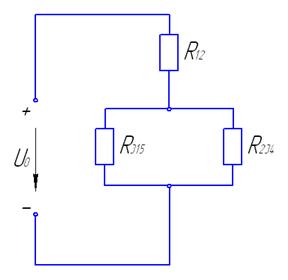 2) 3)
2) 3)
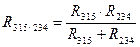
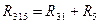
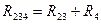
 4)
4)
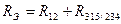
Метод контурных токов
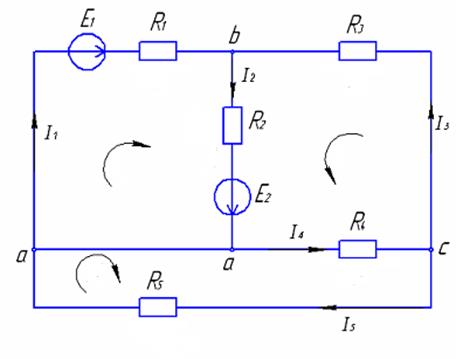 Этот метод заключается в том, что предполагают, что по каждому выделенному независимому контуру протекает свой ток. Будем называть его контурным током. Записываются уравнения по 2 закону Кирхгофа для выделенных контуров, используя контурные токи. Решив эту систему уравнений, находят контурные токи. Реальные токи находятся через контурные. Для этого устанавливается их зависимость от контурных токов.
Этот метод заключается в том, что предполагают, что по каждому выделенному независимому контуру протекает свой ток. Будем называть его контурным током. Записываются уравнения по 2 закону Кирхгофа для выделенных контуров, используя контурные токи. Решив эту систему уравнений, находят контурные токи. Реальные токи находятся через контурные. Для этого устанавливается их зависимость от контурных токов.
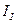
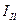
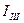
1. Топографический анализ
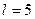 ,
, 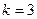 ,
, 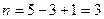
2. Задаемся положительным направлением токов в ветвях
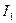 ,
, 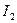 ,
, 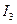 ,
, 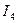 ,
, 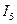 - реальные токи.
- реальные токи.
3. Задаемся положительным направлением контурных токов.
4.  Составляем уравнения по 2 закону Кирхгофа
Составляем уравнения по 2 закону Кирхгофа
I) 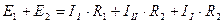
II) 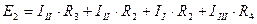
III) 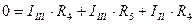
Решая уравнения, находим 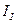 ,
, 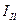 ,
, 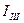 .
.
5. Выражаем реальные токи через контурные
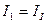 ;
; 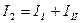 ;
; 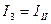 ;
; 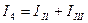 ;
; 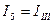 .
.
Вывод: по сравнению с методом непосредственного применения законов Кирхгофа при данном методе система уравнений уменьшается. Она состоит только из уравнений, записанных по 2 закону Кирхгофа. Таким образом, число уравнений будет равно числу независимых контуров.
