Арифметические операции с целыми числами в восьмеричной и шестнадцатеричной системах счисления
Как и в десятичной или двоичной системах счисления все арифметические операции с целыми числами в восьмеричной или шестнадцатеричной системах счисления основаны на таблицах сложения и умножения. Таблицы сложения и умножения в восьмеричной и шестнадцатеричной системах счисления приведены в таблицах 8, 9, 10 и 11.
Таблица 8.
Таблица сложения целых чисел в восьмеричной системе счисления.
Таблица 9.
Таблица умножения целых чисел в восьмеричной системе счисления.
Таблица 10.
Таблица сложения целых чисел в шестнадцатеричной системе счисления.
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | A | B | C | D | E | F | ||||||||||
| B | B | C | D | E | F | 1A | ||||||||||
| C | C | D | E | F | 1A | 1B | ||||||||||
| D | D | E | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1E |
Таблица 11.
Таблица сложения целых чисел в шестнадцатеричной системе счисления.
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | C | E | 1A | 1C | 1E | |||||||||||
| B | F | 1B | 1E | 2A | 2D | |||||||||||
| B | 1C | 2C | 3C | |||||||||||||
| A | F | 1E | 2D | 3C | 4B | |||||||||||
| C | 1E | 2A | 3C | 4E | 5A | |||||||||||
| E | 1C | 2A | 3F | 4D | 5B | |||||||||||
| 1B | 2D | 3F | 5` | 5A | 6C | 7E | ||||||||||
| A | A | 1E | 3C | 5A | 6E | 8C | ||||||||||
| B | B | 2C | 4D | 6E | 8F | 9A | A5 | |||||||||
| C | C | 3C | 6C | 9C | A8 | B4 | ||||||||||
| D | D | 1A | 4E | 5B | 8F | 9C | A9 | B6 | C3 | |||||||
| E | E | 1C | 2A | 7E | 8C | 9A | A8 | B6 | C4 | D2 | ||||||
| F | F | 1E | 2D | 3C | 4B | 5A | A5 | B4 | C3 | D2 | E1 |
Арифметические операции с вещественными числами в двоичной системе счисления.
Арифметические операции с вещественными числами в двоичной системе счисления аналогичны операциям в десятичной системе счисления. Рассмотрим процесс выполнения действий на примерах.
Пример 1.
Дано A(2)=10011,01. B(2)=1,0101 представленные в форме записи с фиксированной запятой. Найти C(2)= A(2)+B(2).
Решение:
Выравниваем количество знаков после запятой: A(2)=10011,0100. B(2)=1,0101
Выполняем операцию сложения
| 10011,0100 +1,0101 |
| 10100,1001 |
Ответ C(2)=10100,1001
Пример 2.
Дано A(2)=0,1001101*10101. B(2)=0,10101*101 представленные в форме записи с плавающей запятой. Найти C(2)= A(2)+B(2).
Решение:
Выравниваем порядки чисел:
A(2)=0,1001101*10101.
B(2)=0,10101*101=0,000010101*10101.
Складываем мантиссы:
Для этого выравниваем количество знаков после запятой: A(2)=0,100110100, B(2)= 0,000010101
Выполняем операцию сложения мантисс чисел представленных в двоичной системе счисления так же как и в случае представления чисел в форме записи с фиксированной запятой
| 0,100110100 +0,000010101 |
| 0,101001001 |
В результате сложения мантисс получили результат: 0,101001001. Дописываем показатель и получаем ответ.
Ответ C(2)=0,101001001*10101.
Операции умножения вычитания и деления производятся по аналогичному алгоритму.
Логические операции.
В информатике под понятием логическим операции понимают результат сравнения по какому либо правилу заданных величин и выдачу ответа имеющего всего два значения истина и лож. Вся работа любой вычислительной техники основана на выполнении логически операций и операций переноса. Правила, определяющие результат выполнения логической операции, то есть результаты, которые получаться в результате выполнения функции с конкретными исходными данными называются таблицами истинности.
Существует три основных закона логического сравнения величин это И(and), ИЛИ(or) и НЕ(not). Схематическое представление элементов выполняющих логические операции и соответствующие им таблицы истинности представлено в таблице 12.
Таблица 12. Описание логических элементов вычислительной техники.
| Операция | Элемент | Таблица истинности | |||
| Логическое произведение (конъюнкция). Операция «И». Результат логической суммы совпадает с результатом арифметического произведения. Результат будет равен истина, только в случае, если оба аргумента равны единице. |  | A | B | A И Б | |
| Логическая сумма (дизъюнкция). Операция «ИЛИ». Результат логической суммы, отличается от результата суммы двух одноразрядных двоичных чисел. Результатом будет истина, если хотя бы один входной аргумент равен единице. |  | A | B | A ИЛИ B | |
| Логическое отрицание(инверсия). Операция «НЕ» Результатом логической операции отрицание будет изменение значения входного аргумента: истина на лож и обратно. |  | A | НЕ A | ||
Этих трех элементов логических функций и операций переноса(сдвига) достаточно, для тог, чтобы организовать любую операцию арифметического вычисления или сравнения чисел в двоичной системе счисления.
Под сдвигом понимается смещение разрядов двоичного числа в право или в лево, в зависимости от указанного направления. Освободившееся после сдвига место заполняется нулями. В любой позиционной системе счисления сдвиг в лево(<<) на один разряд означает умножение на основание системы счисления, а сдвиг в право(>>) на один разряд - деление на основание системы счисление.
Пример 1.
Дано A(10)=123. Умножить число с помощью операции сдвига на 100(10).
Решение:
100=102 следовательно для умножения заданного числа на 100 необходимо выполнить сдвиг на два разряда в лево
A(10)=123*100=123 << 2=12300
Ответ A(10)=12300.
Пример 2.
Дано A(10)=345. Разделить число с помощью операции сдвига на 1000(10).
Решение:
Для выполнения операции деления на 1000 необходимо умножить исходное число на 1/1000
1/1000=0,001=10-3 следовательно для деления заданного числа на 1000 необходимо выполнить сдвиг на три разряда в право
A(10)=345/1000=345 >> 3=0,345
Ответ A(10)=0,345.
Пример 3.
Дано A(2)=11010. Умножить число с помощью операции сдвига на 100(2).
Решение:
100=22 следовательно для умножения заданного числа на 100 необходимо выполнить сдвиг на два разряда в лево
A(10)= 11010*100=11010 << 2=1101000
Ответ A(2)= 1101000.
Пример 4.
Дано A(2)=11010. Разделить число с помощью операции сдвига на 10 (2).
Решение:
Для выполнения операции деления на 10 необходимо умножить исходное число на 1/10
1/10=0,1=10-1 следовательно для деления заданного числа на 10 необходимо выполнить сдвиг на один разряда в право
A(10)=11010/10=11010 >> 1=1101
Ответ A(2)=1101.
Поскольку двоичная система счисления состоит всего из двух чисел {0,1} принято считать, что 0(2) в логических функциях представляет собой лож, а 1(2) истину. Исходя из этого при помощи логических элементов можно организовать любой вычислительный процесс. Рассмотрим процесс сложения двоичных чисел на примере двухразрядного сумматора рисунок 9.
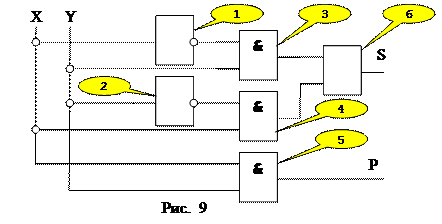
Для понимания принципа использования логических функций построим таблицу истинности получающуюся при выполнении процесса сложения для всех элементов таблица 13.
Таблица 13. Процессы происходящие в двухразрядном сумматоре.
| X | Y | (не X) | (не Y) | (Y и 1) | (X и 2) | (XиY) | (3или4) | S | P |
На схеме приведенной на рисунке 10 на вход сумматора поступает два одноразрядных числа записанных в двоичной системе счисления. На выходу получаем одно двухразрядное число представляющее собой сумму одноразрядных чисел записанных на входе. Преобразуем таблицу 13 в таблицу истинности для сложения одноразрядных чисел, записанных в двоичной системе счислении, таблица 14.
Таблица 14.
Результат работы сумматора, основанного на выполнении логических операций.
| X | Y | PS |
В результате получили таблицу истинности, аналогичную таблице выполнения операции сложения в двоичной системе счисления таблица 6.
Аналогичным образом организованы и другие математические операции в устройствах вычислительной техники.
