Фигура (граф), которую можно начертить, не отрывая карандаш от бумаги, называется уникурсальной

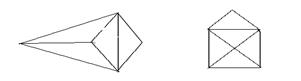
рис.6 (Эйлеровы графы)

Связные графы

Граф называется связным, если любые две его вершины могут быть соединены путем, т. е. последовательностью ребер, каждое следующее из которых начинается в конце предыдущего.

Граф называется несвязным,если это условие не выполняется.

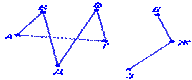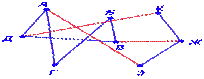рис.7 рис.8

На рисунке 7, очевидно, изображен несвязный граф. Если, например, на рисунке между вершинами Д и Е провести ребро, то граф станет связным. (рис.8) Такое ребро в теории графов (после удаления которого граф из связного превращается в несвязный) называется мостом.Примерами мостов на рисунке 7 могли бы служить ребра ДЕ, A3, ВЖ и др., каждое из которых соединяло бы вершины «изолированных» частей графа. (рис.8)

Несвязный граф состоит из нескольких «кусков». Эти «куски» называются компонентами связности графа. Каждая компонента связности является, конечно, связным графом. Отметим, что связный граф имеет одну компоненту связности.

ТЕОРЕМА. Граф является эйлеровым тогда и только тогда, когда он связен и имеет не более двух нечетных вершин.

Доказательство:

Рисуя граф каждую вершину, за исключением начальной и конечной, мы войдём столько же раз, сколько выйдем из неё. Поэтому степени всех вершин должны быть чётными, кроме двух, а значит, эйлеров граф имеет не более двух нечётных вершин.

Деревья

Деревом называется любой связный граф, не имеющий циклов. Договорились считать «деревом» и всякий граф, состоящий из одной (изолированной) вершины.

Цикломназывается путь, в котором совпадают начало с концом.

Если все вершины цикла разные, то такой цикл называется элементарным(или простым) циклом. Если же цикл включает в себя все ребра графа по одному разу, то такой цикл называется Эйлеровой линией (рис.9а). В графе на рис.9б два цикла: 1-2-3-4-1 и 5-6-7-5.

Путемв графе от одной вершины к другой называется

такая последовательность ребер, по которой можно проложить маршрут между этими вершинами.

При этом никакое ребро маршрута не должно встречаться более одного раза. Вершина, от которой проложен маршрут, называется началом пути, вершина в конце маршрута — конец пути.

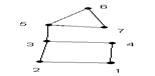
рис.9а;б

Висячей вершиной называется вершина, из которой выходит ровно одно ребро. (рис.10)

рис.10 (кружком обведены висячие вершины)

Свойство 1. Для каждой пары вершин дерева существует единственный путь, их соединяющий.
Этим свойством пользуются при нахождении всех предков в генеалогическом дереве, например, по мужской линии, любого человека, чья родословная представлена в виде генеалогического дерева, которое является «деревом» и в смысле теории графов.

Свойство 2. Всякое ребро в дереве является мостом.

Действительно, после удаления любого ребра дерева, оно «распадается» на два дерева.