Определение скорости передачи полезной информации и оптимальной длины кадра

Проведенный только что простой анализ производительности дает также оценку наиболее предпочтительной длины пакетов (информационного поля в кадре данных), применяемых в сети. В большинстве сетей она выбирается равной около 1000 бит.

Обозначим длину пакета в кадре, выражаемую числом разрядов, через l, а число остальных разрядов, используемых в других полях через l’ (см.
рис. 5.23) [43].

Рис. 5.23. Формат кадра

Пусть передающая станция А находится в состоянии насыщения и передает 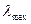кадров/с. Средняя скорость данных в бит/с, поступающих на принимающую станцию В, на основании выведенных в предыдущем пункте формул, равна

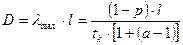(5.7)

Принимая t_k = (l + l’)/C, где С - пропускная способность канала в бит/с, для нормированной скорости поступления данных получим

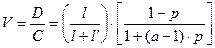(5.8)

Это выражение ясно показывает влияние на скорость передачи данных длины пакета l, длины управляющего поля l’ и вероятности ошибки. Длительность перерыва описывается нормированным параметром а.

Пусть р_в - вероятность искажения бита. Тогда вероятность ошибки в кадре определяется равенством

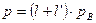при а=1 (5.9)

Подставим полученное выражение в (4.2) и продифференцируем dv/dl. В результате оптимальная длина пакета равна

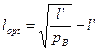(5.10)

и не зависит от а.

Методы случайного доступа к сети

Двумя основными способами доступа к общей среде передачи являются управляемый доступ с применением опроса и случайный доступ. В свою очередь существуют различные типы стратегий случайного доступа.

Методы случайного доступа полностью децентрализованы. Пользователь может передавать когда угодно, лишь с незначительными ограничениями, зависящими от метода доступа.

Из-за случайности моментов времени, в которые пользователи могут решить начать передачу, независимо от метода не исключена возможность того, что два или несколько пользователей могут выйти на связь в пересекающиеся промежутки времени. Это приводит к столкновениям (коллизиям), которые сначала должны быть распознаны, а затем разрешены. При увеличении нагрузки увеличивается и вероятность коллизий, что приводит к возможной неустойчивости работы рассматриваемых механизмов.

В результате производительность ограничивается некоторым максимальным значением, меньшим пропускной способности канала, и это значение в каждом случае зависит от первоначального механизма доступа и алгоритма разрешения коллизий.

Методы Алоха

Сначала методы случайного доступа были предложены для случаев, когда большое число пользователей пытаются довольно редко передать пачки сообщений или, когда друг с другом связываются небольшое число ЭВМ. Но применимо к производственным процессам, которые требуют строгого управления задержкой доступа, более предпочтителен управляемый доступ. Рассмотрим два простейших типа стратегии случайного доступа: чистую Алоху и синхроннуюАлоху [43].

Чистая Алоха

Эта схема сначала была применена для доступа к общему каналу сотрудниками Гавайского университета в начале 1970-х годов. По этой схеме пользователь, желающий передать сообщение, делает это когда угодно. В результате могут наложится во времени два или несколько сообщений, вызвав столкновение (коллизию).

Распознавание коллизий и сообщение о них пострадавшим пользователям в первоначальной системе Алоха направлялись по радио на центральный пункт. Также это могло осуществляться путем применения положительгых подтверждений в сочетании с перерывом. При обнаружении столкновения пострадавшие станции предпринимают попытки повторной передачи потерянного сообщения, но они должны распределять время попыток случайным образом, следуя некоторому алгоритму столкновения нового конфликта.

Стратегия доступа типа Чистой Алохи позволяет добиться производительности самое большее 1/2e » 0,18 пропускной способности канала. Введем сначала некоторые определения. За доступ к каналу состязаются N станций. Станция передает, в среднем, l пакетов в секунду (интенсивность обращений к сети). Величина 1/m представляет собой пропускную способность канала (m) в передаваемых пакетах в секунду. Рассмотрим теперь частный случай, при котором все передаваемые сообщения (пакеты) имеют среднюю длину t, соответствующую m единицам времени передачи. Будем считать, что интенсивность нагрузки S (эквивалентно r -нормированной по mнагрузке) характеризует использование канала вновь поступающими пакетами

S º r = Nlm

Величина 1/t, которая обозначается m, представляет собой пропускную способность канала в передаваемых пакетах в секунду. Таким образом, Nl/m = Nlm - относительное использование канала, или производительность, нормированная относительно каждого компьютера одинакова. Общая интенсивность пакетов, передаваемых в канал, включая вновь генерируемые и передаваемые повторно, имеет некоторое значение l’ > l (из-за коллизий от каждого компьютера будет передаваться больше сообщений из-за необxодимости возобновлять поток). Тогда фактическая интенсивность нагрузки, или использование канала, является параметром G, который равен

G = Nl’t.

Рассмотрим типичное сообщение длительностью t с, показанное на рис. 5.24.

Ошибка! Ошибка связи.

Рис. 5.24. Столкновение двух сообщений

Оно подвергается столкновению с другим сообщением, если эти два сообщения будут наложены одно на другое в любой точке. Легко заметить, передвигая пунктирное сообщение во времени, что столкновение может произойти в промежутке времени продолжительностью 2t с. Вероятность того, что в промежутке 2t с не произойдет столкновения, равна e^-2Nl’m=e^-2G.

Отношение S/G представляет долю сообщений из числа передаваемых в канал, которые проходят успешно. Это число должно быть равно вероятности отсутствия столкновений. Таким образом уравнение производительности для чистой Алохи:

S = Ge^-2G (5.11).

Здесь S - нормированная производительность (средняя скорость поступления пакетов, деленная на максимальную производительность 1/m), а G - нормированная пропущенная нагрузка. Таким образом, S – независимая переменная, а G - ее функция. График зависимости G от S имеет вид двузначной кривой (рис. 5.25).

Ошибка! Ошибка связи.

Рис. 5.25. Характеристика производительности; чистая Алоха

Отметим, что S имеет максимум S = 0,5e^-1» 0,18 при G = 0.5. Судя по формуле (4.11) или кривой при малой поступающей нагрузке S столкновения происходят редко, и G » S. Когда S начинает расти, приближаясь к максимальному значению 0.18, число столкновений быстро увеличивается, что ведет в свою очередь к росту вероятности столкновения. Система теряет устойчивость, S падает, а G увеличивается до больших значений.

Синхронная Алоха

Максимально возможная производительность схемы чистой Алохи может быть удвоена с помощью простого приема пазметки шкалы времени и разрешения пользователям начинать попытки передачи сообщений только в начале каждого временного интервала m (равного длительности сообщения). Эта схема требует, чтобы работа всех пользователей системы была синхронизирована во времени. Пример работы такой системы показан на рис. 5.26, на котором одно сообщение передано успешно, а с другим произошло столкновение.

Ошибка! Ошибка связи.

Рис. 5.26. Передача при синхронной Алохе

Поскольку сообщения могут быть переданы только в размеченные промежутки времени, столкновения происходят лишь когда одна или несколько попыток передачи совершаются в том же промежутке.

Вероятность успешной передачи задается в виде e^-G, а производительность для синхронной Алохи имеет вид

S = Ge^-G.

Нормированная производительность S достигает максимального значения 1/e » 0,368 при G = 1. Зависимость пропущенной нагрузки от производительности для синхронной Алохи показана на рис. 5.27, где она сравнивается с соответствующей зависимостью для чистой Алохи.

Из приведенной характеристики очевидно, что ввиду двух возможных значений G при заданной производительности S, для этой системы доступа также характерна неустойчивость.

Ошибка! Ошибка связи.

Рис. 5.27. Характеристика производительности; синхронная Алоха