Теория Опыта Резерфорда

Выше мы дали общие определения величин, определяемых в опытах по рассеянию.

Теперь мы вернемся к основной нашей проблеме, к рассеянию a-частиц и еще раз опишем исторический опыт Резерфорда.

Итак, пучок a-частиц, вылетающих из радиоактивного источника со скоростью ~ 10⁹см/с направлялся на мишень, представляющую собой тонкую золотую фольгу толщиной в 1 мкм, что составляет примерно 10⁴ атомных слоев. Флуоресцирующий экран, поставленный за мишенью, вспышками отсчитывал число a-частиц, прошедших через мишень и рассеившихся на угол q. Как уже раньше отмечалось, подавляющее число a-частиц отклонялось на малые углы, в среднем 2^о-3^о.

Однако, примерно одна a-частица на 10⁴ падающих на мишень, отклонялась на большой угол, в том числе были и такие, которые рассеивались назад, почти на 180^о. Было также замечено, что рассеяние на малые углы происходит в соответствии с законом нормального распределения случайных величин.

Теперь, следуя рассуждениям Резерфорда, объясним полученные закономерности и, в частности, ответим на вопрос о том, какая модель соответствует действительности, Томсона или Резерфорда.

Ясно, что если бы мишень состояла из твердых шариков, то ни одна из a-частиц не могла бы пройти через 10⁴ слоев такого вещества.

Рассмотрим два случая: а) мишень построена из атомов Томсона, б) мишень построена из атомов Резерфорда.

Модель Томсона. Атом Томсона - это положительно заряженная "капелька" в которую вкраплены электроны, поэтому эта система уже на небольшом расстоянии от нее нейтральна, как и положено атому, a-частицы могут проникнуть в такую каплю. Они могут рассеяться как на положительном заряде капли, с максимумом электрической напряженности на ее поверхности, так и на электронах внутри этой "капли". Каждая "капля" имеет радиус R~10^-8см.

Расчеты показывают, что средний угол рассеяния a-частицы с энергией 5 МэВ на атоме Томсона составит очень малую величину ~ (0,02 - 0,03)^о.

Если в мишень из 10⁴ слоев атомов Томсона пустить a-частицу, то в результате многократных столкновений (в каждом слое она будет испытывать столкновения, равновероятно отклоняющие ее вправо и влево, вверх и вниз), по вылете из мишени a-частица "наберет" средний угол >> угла рассеяния в одном столкновении. Большая часть пучка a-частиц будет вылетать под углами (2-3)^о.

Резерфорд вычислил вероятность рассеяния a-частицы в такой среде на угол 180^о (т.е. учел столь невероятный случай, когда почти при каждом столкновении a-частица отклоняется все время в одну сторону). Вероятность такого случая составляет величину ~ 10^-3000 . Т.о. ожидать хотя бы и редких, но больших углов в мишени Томсона бессмысленно.

Модель Резерфорда. Атом Резерфорда представляет собой малый тяжелый керн (ядро), окруженный облаком электронов. Следует подчеркнуть, что на момент постановки эксперимента постулаты Бора еще не были сформулированы, поэтому такая модель вызывала определенные сомнения.

Если рассмотреть рассеяние a-частицы на атоме Резерфорда, то следует учесть возможность рассеяния как на внешних электронах, так и на ядре. Рассеяние на электронах столь же мало, что и на атоме Томсона, т.е. составляет (0,02-0,03)^о на отдельном атоме. Рассеяние на ядре (если масса ядра >> массы a-частицы) может привести к большим углам, в том числе и 180^о.

Проследим движение a-частицы в мишени из атомов Резерфорда. Поскольку размеры атома составляют величину ~ 10^{-8 см, то мишень из 104}слоев должна быть полностью перекрыта атомами. Однако, поскольку a-частица движется с большой скоростью, то она испытывает лишь еле заметные отклонения в электронной оболочке атома. Таким образом, если a-частица случайно не натолкнулась на ядро, то она движется также, как и в мишени Томсона, многократно рассеиваясь и набирая средний по вылету из мишени угол рассеяния (2-3)^о. Однако, в отличие от мишени Томсона, a-частица может столкнуться с тяжелым ядром. Такое столкновение значительно менее вероятно, чем столкновение с атомом в целом, потому что ядро (как выяснилось) на 4-5 порядков меньше атома. В то же самое время вероятность столкновения с ядром и отклонение на большой угол значительно больше, чем вероятность отклонения на большой угол в мишени Томсона. Таким образом, все экспериментальные результаты полностью объяснились с позиций модели Резерфорда.

Мы рассмотрели качественно свойства модели Резерфорда, и уже из этого описания видно, что доказательства правильности этой модели не столь просты, как кажется на первый взгляд. Ниже мы весьма кратко обсудим математическую модель рассеяния быстрой a-частицы, поскольку эти задачи подробно описываются в ряде книг [1, 2, 3].

Рассеяние на одном центре. Формула Резерфорда. Важным условием проведения эксперимента является требование на толщину L мишени. Мишень должна быть "тонкой". Это означает, что средняя длина свободного пробега l при рассеянии на ядрах должна удовлетворять требованиям:

l >>L (6).

Это условие обеспечивает однократность столкновения a-частицы с ядрами мишени (хотя в мишени имеется 10⁴ атомных слоев).

Следует подчеркнуть, что величина дифференциального сечения I(q), как подчеркивалось ранее, не зависит от числа рассеивающих центров, поэтому эту величину мы будем рассматривать в случае рассеяния a-частицы на одном рассеивающем центре. Важнейшим элементом в теории рассеяния является выбор потенциала рассеяния U(r). Эта величина является характеристикой свойств вещества мишени и не зависит от условий эксперимента. Резерфорд выбрал кулоновский потенциал, положив U(r)=Ze/r. Для простоты в качестве рассеивающего центра мы примем ядро золота, масса которого много больше массы a-частицы, поэтому отдачей ядра можно будет пренебречь.

На рис.2 изображены две близкие траектории a-частицы в поле ядра (заряд +Ze), находящегося в начале координат. Траектории отличаются значениями прицельного параметра b - расстояния до оси слева на рисунке, соответствующего положению a-частицы, когда она находится вдали от ядра. q - угол рассеяния. Задача имеет цилиндрическую симметрию с азимутальным углом j.

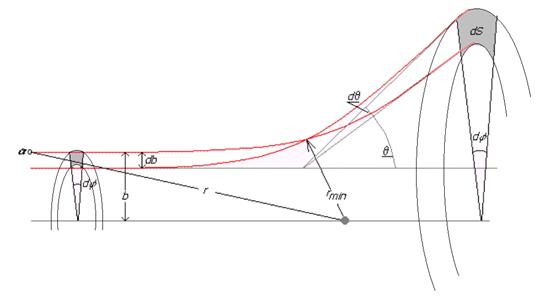
Рис.2 Схема рассеяния a-частицы на ядре.

Расчет траектории движения a-частицы в кулоновском поле показывает, что ее траектория - гипербола, при этом прицельный параметр b связан с углом рассеяния q формулой:

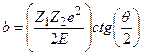(7)

где Z₂e - заряд частицы-мишени (неподвижный рассеивающий центр), Z₁e - заряд a-частицы (Z₁=2), Е - энергия a-частицы.

Минимальное расстояние при сближении a-частицы с рассеивающей частицей (рис.2):

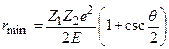(8)

Теперь вернемся к определению дифференциального сечения (3) и преобразуем его к виду рассеяния на одном центре:

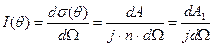, (9)

где 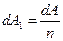, т.е. число рассеянных a-частиц в единицу времени на одном центре. Такое представление нам удобно для того, чтобы связать измеренный макроскопический параметр - угол рассеяния q с микроскопическим (неизмеряемым) параметром - прицельным параметром b.

Нетрудно видеть, что частицы, попавшие в площадку dS, обязательно пройдут через элемент площади bdb кольца, расположенного на расстоянии b от оси, на которой находится рассеивающий центр. Число частиц, прошедших через этот элемент площади в единицу времени, равно

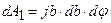(10)

Отсюда

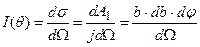(11)

Если проинтегрировать по j от 0 до 2p, то ds будет представлять собой площадь пояса, изображенного слева на рис.2. Поскольку b - микроскопический, неизмеряемый параметр, воспользуемся формулой (7) и выразим ds через измеряемую величину - угол рассеяния q. В результате будем иметь:

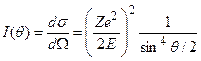(12)

где dW=dS/R²=sinq dq dj, а R - расстояние до площадки dS. Здесь учтено, что Z₁=2, Z₂=Z – атомный номер ядра мишени. Соотношение (12) есть известная формула Резерфорда.

Полученная формула определяет зависимость дифференциального сечения от угла рассеяния. Качественные рассуждения о роли многократных столкновений дают возможность восстановить картину движения a-частицы в веществе мишени. a-частица всегда испытывает многократные столкновения, приводящие к разбросу в среднем в 2^о-3^о. В этой области углов рассеяние по Резерфорду практически не дает вклада. Начиная с углов рассеяния в 5^о-6^о, наоборот, резерфордовское рассеяние становится превалирующим. Таким образом, до столкновения с ядром и после столкновения a-частица двигается практически прямолинейно. Поскольку ядра очень малы, то мишень почти прозрачна для a-частиц, которые лишь изредка (и в силу условия l>>L однократно) сталкиваются с ядрами.

Опыт Резерфорда

Учебный лабораторный комплекс представляет собой действующую модель, функционально не отличающуюся от своего базового прототипа. Конструктивно УЛК ОР предоставляет возможность пользователю работать с использованием и без использования компьютера.

Базовая установка.

Базовая установка представляет собой вакуумированную камеру (камера рассеяния), в которой находится в соответствии со схемой (рис.1) источник a-частиц (Pu²³⁸), энергетический спектр которого состоит из двух тесно расположенных линий 5491 кэВ и 5450 кэВ. Первая по интенсивности составляет ~ 65%, а вторая - 35 % . Средневзвешенное значение Е_a» 5,48 МэВ (рис.3).

Поскольку при столкновении a-частиц с молекулами воздуха a-частицы заметно теряют свою энергию, то камера рассеяния должна быть откачана до давления ~ 1 мм ртутного столба.

Мишенью служит золотая пленка толщиной » 1 мкм.

Подвижный полупроводниковый детектор регистрирует попадающие в него a-частицы. Сигналы с детектора через зарядо-чувствительный усилитель попадают либо на пересчетную схему, либо на специальную спектрометрическую плату, вмонтированную в системный блок компьютера. На экран компьютера выводится спектр рассеянных частиц.

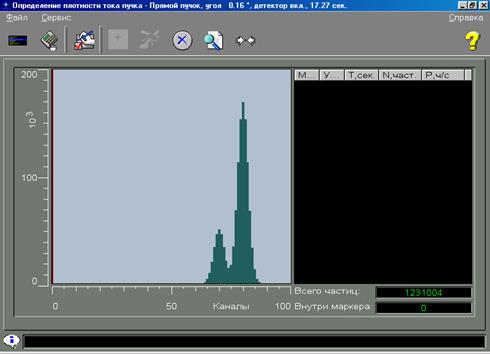
Рис. 3. Спектр альфа-линий Pu²³⁸.