Практическая работа 20. Решение алгоритмических задач

Задачи:

1. Вася действует по следующему алгоритму:
Шаг 1. Пройти 10 м прямо.
Шаг 2. Повернуть направо.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 50 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой Вася начал свое движение, составит … Обоснуйте свой ответ.

2. Нарисуйте блок-схему к алгоритму, представленному в задаче 1. Какую структуру имеет алгоритм? Почему?

3. Дан алгоритм:

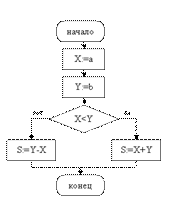
Подсчитать S для следующих значений a и b:

№ варианта
a=
b=

Практическая работа 21. Конечные автоматы

Задание 1. Конечный автомат задан диаграммой. Определить входной алфавит 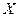, выходной алфавит 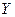, внутренний алфавит , систему команд автомата:

Задание 2. Для автомата 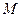найти минимальный :

	,	,	,	,	,	,	,
	,	,	,	,	,	,	,
	,	,	,	,	,	,	,

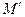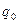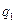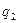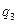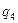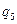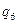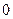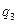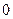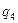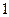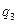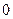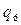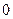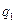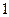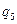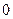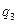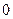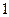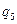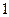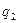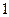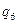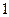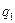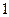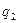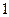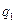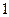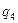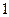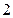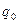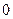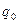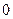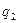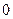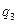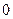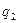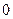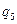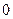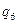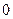Задание 3. Определить последовательность 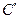, в которую преобразуется заданная последовательность 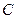, в результате работы автомата:

1) автомат из упражнения II, при , ;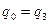

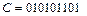Практическая работа 22. Разработка программ для машины Тьюринга

Вариант 1

На информационной ленте машины Тьюринга содержится массив символов +. Необходимо разработать функциональную схему машины Тьюринга, которая каждый второй символ + заменит на –. Каретка в состоянии q₀ находится где-то над указанным массивом.

Вариант 2

Дано число n в восьмиричной системе счисления. Разработать машину Тьюринга, которая увеличивала бы заданное число n на 1.

Вариант 3

Дана десятичная запись натурального числа n>1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1. При этом запись числа n–1 не должна содержать левый нуль, например, 100–1=99, а не 099. Начальное положение головки — правое.

Вариант 4

Дан массив из открывающихся и закрывающихся скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок. Например, дано : « ) ( ( ) ( ( ) », надо получить : « ) . . . ( ( . ».

Вариант 5

Дана строка из букв « a » и « b » . Разработать машину Тьюринга , которая переместит все буквы « a » в левую, а буквы « b » — в правую части строки. Каретка находится над крайним левым символом строки.

Вариант 6

Даны два целых положительных числа в десятичной системе счисления. Сконструировать машину Тьюринга, которая будет находить разность этих чисел, если известно, что первое число больше второго, а между ними стоит знак –. Каретка находится над левой крайней цифрой левого числа.

Вариант 7

Даны два целых положительных числа в различных системах счисления, одно — в троичной системе , другое — в десятичной. Разработать машину Тьюринга, которая будет находить сумму этих чисел в десятичной системе счисления.

Вариант 8

Сконструировать машину Тьюринга, которая выступит в качестве двоично-восьмиричного дешифратора.

Вариант 9

Дана конечная последовательность меток, записанных в клетки ленты подряд, без пропусков. Необходимо разработать машину Тьюринга, которая будет записывать в десятичной системе счисления число этих меток.

Вариант 10

На информационной ленте машины Тьюринга в трех секциях в произвольном порядке записаны 3 различные буквы: A, B и C. Каретка в состоянии q₀ обозревает букву, расположенную справа. Необходимо составить функциональную схему машины Тьюринга, которая сумеет поменять местами крайние буквы.

Вариант 11

Даны два натуральных числа m и n, представленных в унарной системе счисления. Соответствующие наборы символов « | » разделены « – » , вслед за последним символом набора n стоит знак «=». Разработать машину Тьюринга, которая будет находить разность чисел m и n .При этом результат должен быть записан следующим образом : если m>n , то справа от «=» должны стоять знак «+» и набор символов « | » в количестве m–n; если m=n, то справа от знака «=» должна стоять пустая клетка; если m<n, то справа от «=» должны стоять знак «–» и набор символов « | » в количестве n–m.

Вариант 12

Даны два натуральных числа n и m, заданных в унарной системе счисления. Числа n и m представлены наборами символов « | » , разделенных « \ ». В конце набора стоит «=». Разработать машину Тьюринга, которая будет производить деление нацело двух натуральных чисел n и m и находить остаток от деления. При этом результат должен быть записан следующим образом: после «=» должен находиться набор символов « | » частного (он может быть и пустым), после чего ставится знак «(», за которым следует набор символов « | » остатка от деления n на m.

Вариант 13

На ленте машины Тьюринга находится число, записанное в десятичной системе счисления. Умножить это число на 2, если каретка находится над крайней левой цифрой числа.

Вариант 14

На ленте машины Тьюринга находится целое положительное число, записанное в десятичной системе счисления. Найти произведение этого числа на число 11. Каретка обозревает крайнюю правую цифру числа.

Вариант 15

На ленте машины Тьюринга находится десятичное число. Определить делится это число на 5 без остатка. Если делится, то записать справа от числа слово «да», если нет — «нет». Каретка находится где-то над числом.

Вариант 16

На ленте машины Тьюринга записано число в десятичной системе счисления. Каретка находится над крайней правой цифрой. Записать цифры этого числа в обратном порядке.

Вариант 17

На информационной ленте машины Тьюринга находится десятичное число. Найти результат целочисленного деления этого числа на 2.