Вращающиеся системы координат

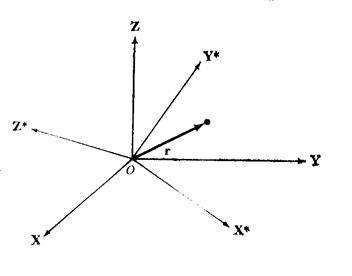
Рисунок 11.1. Вращающаяся система координат

Рассмотрим две системы координат (рис. 11.1): 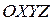- неподвижная инерционная система координат, 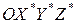- вращающаяся система координат. Начала этих координат совпадают и расположены в точке О, а оси 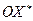, , 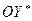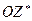вращаются относительно осей , , .

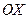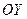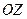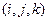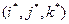Пусть и - тройки единичных векторов, направленных вдоль основных осей систем 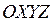и 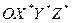соответственно. Положение точки r, неподвижной относительно системы координат 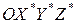, можно описать следующими двумя способами:

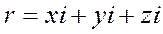, (11-1)

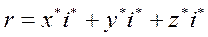. (11-2)

Найдём скорость точки r. Поскольку обе системы координат взаимно вращаются, скорость точки r(t) будут различны в этих системах. Примем, что 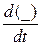- скорость в неподвижной системе координат 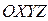; (11-3)

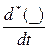- скорость в подвижной вращающейся системе

координат 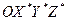. (11-4)

Тогда из выражения (11-1) получаем скорость точки r(t) в системе координат :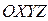

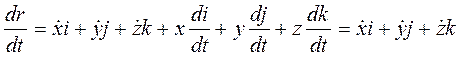. (11-5)

Дифференцируя равенство (11-2), получаем скорость точкиr(t) в системе координат :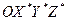

.

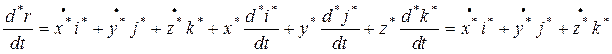(11-6)

С учетом равенств (11-2) и (11-6) получим следующее выражение для скорости точки r(t) в системе координат :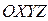

.

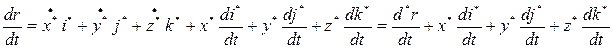(11-7)

Здесь трудно вычислить производные 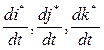, в связи с тем что векторы 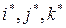вращаются относительно векторов .

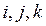Чтобы найти соотношения между скоростями точки r в неподвижной и вращающейся системах координат, предположим, что система 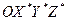вращается вокруг некоторой оси OQ, проходящей через точку О с угловой скоростью 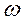(рис. 11.2).

Угловая скорость вращения системы 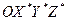представляет собой по определению вектор длины , направленный вдоль оси OQ в соответствии с правилом правой руки.

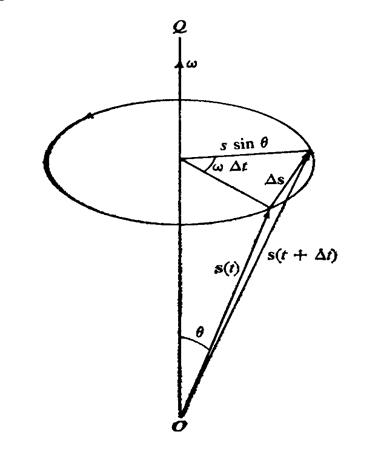
Рисунок 11.2. Скорость во вращающейся системе координат

Скорость точки, положение которой задаётся вектором s в системе координат равна:

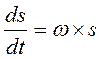. (11-8)

Поскольку производная вектора определяется равенством:

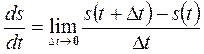, (11-9)

справедливость выражения (7-8) можно доказать, убедившись, что:

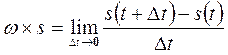. (11-10)

Поскольку равенство векторов обеспечивается совпадением их длин и направлений, векторы в левой и правой частях равенства (11-10) одинаковы по величине и их направления совпадают. Длина вектора 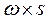равна:

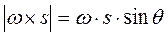. (11-11)

Если величина 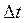достаточно мала, то из рис. 11.2 очевидно, что:

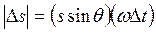. (11-12)

Следовательно, длина векторов в левой и правой частях равенства (11-10) равны. В соответствии с определением векторного произведения вектор 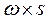перпендикулярен вектору s и лежит в плоскости окружности (рис. 11.2).

Применив формулу (11-8) к единичным векторам 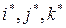из равенства (11-7), получаем:

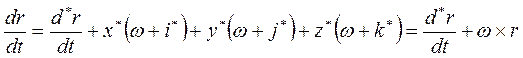. (11-13)

Это основное соотношение, определяющие связь между скоростями одной и той же точки во вращающейся и неподвижной системах координат. Продифференцировав левую и правую части равенства (11-13), получим:

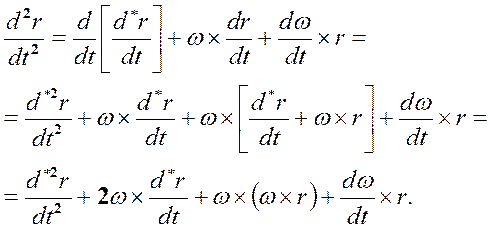(11-14)

Равенство (11-14) представляет собой теорему Кориолиса. Первое слагаемое в правой части – ускорение точки в системе 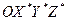. Второе слагаемое описывает кориолисово ускорение. Третье слагаемое – центростремительное ускорение, направленное к оси вращения и перпендикулярное ей. Четвёртое слагаемое исчезает при постоянной угловой скорости.

Лекция 12