Перевод правильной десятичной дроби в любую другую позиционную систему счисления

Основные понятия

Система счисления – это совокупность правил наименования и изображения чисел с помощью набора символов, называемых цифрами.

Используются три типа систем счисления:

· позиционная – представление числа зависит от порядка записи цифр.

· непозиционная – представление числа не зависит от порядка записи цифр

· смешанная – нет понятия «основание»: либо оснований несколько, либо оно вычисляемое

В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позициив записи числа.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7∙10² + 5∙10¹ + 7∙10⁰ + 7∙10^-1 = 757,7.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

a_n-1 q^n-1 + a_n-2 q^n-2+ ... + a₁ q¹ + a₀ q⁰ + a_-1 q^-1 + ... + a_-m q^-m,

где a_i – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.

Таблица 1. Эквиваленты чисел в различных системах счислений

Системы счисления
Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
			A
			B
			C
			D
			E
			F

Преобразование чисел из одной системы счисления в другую

Перевод целого числа из десятичной системы в другую позиционную систему счисления

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

a. в двоичную:

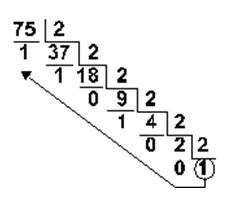
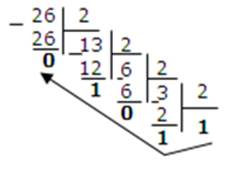
75₁₀ = 1 001 011₂ 26₁₀=11010₂

b. в восьмеричную:

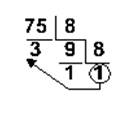
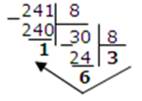
75₁₀= 113₈ 241₁₀=361₈

c. в шестнадцатеричную:

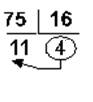
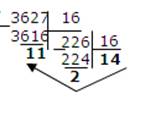
75₁₀= 4B₁₆ 3627₁₀=Е2В₁₆

Перевод правильной десятичной дроби в любую другую позиционную систему счисления

При переводе правильной десятичной дроби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения.

Умножение производится до тех пор, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности.

a. в двоичную:

0,35₁₀ = 0,01011₂ 0,5625₁₀=0,1001₂

или

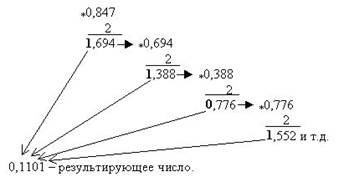
0,847₁₀=0,1101₂

b. в восьмеричную:

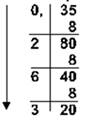
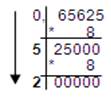
0,35₁₀ = 0,263₈ 0,65625₁₀=0,52₈

c. в шестнадцатеричную:

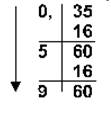
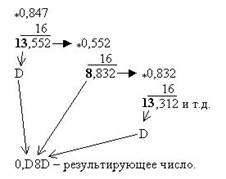
0,35₁₀= 0,59₁₆ 0,847₁₀=0,D8D₁₆