Методы стратификации (расслаивания) данных
Автор статьи: Губарев Андрей Викторович, кандидат технических наук.
При изучении причин, влияющих на исследуемые процесс, показатель, проблему и т.д. часто применяется метод стратификации или расслаивания.
Все получаемые во время исследования данные можно поделить на несколько групп, в зависимости от обстоятельств, во время которых происходил сбор информации. Вот эти группы мы и будем называть стратами или слоями.
Таким образом, процесс стратификации (расслаивания) заключается в разделении информации на страты или слои, которыми могут быть дни недели, часы, оборудование, операторы и т.д.
Так как все регистрируемые данные подвержены изменчивости, то их расслаивание по соответствующим факторам может пролить свет на причину разброса исследуемой характеристики или параметра, ведь один из них как раз и может быть той самой причиной.
Не всегда причина бывает единственной, на самом деле правильнее будет сказать, что она никогда не бывает единственной. Используя метод расслаивания можно оценить степень влияния разных факторов на исследуемую проблему.
Для упрощения работы разработано несколько методик расслаивания, которые можно применить практически ко всем сферам деятельности.
В сфере производства применяются методы расслаивания 5М, 6М, 7М, 8М и 9М. В сфере оказания услуг нашла применение методика 5Р.
В методе с обозначением «М» стратификация происходит по факторам, названия которых начинаются с английской буквы «М».
В методе 5М расслоение проводят по следующим факторам:
1) Человек (man) (человек);
2) Машины, оборудование (machines);
3) Материалы, сырье, комплектующие (materials);
4) Измерения (measure);
5) Метод, технология (method).
В методе расслаивания 6М в дополнение к 5М вводится производственная среда (Media). Метод 7М получается добавлением к 6М такого фактора как техническое обслуживание или поддержка (maintenance). Далее метод расслаивания развивается до 8М путем добавления фактора «деньги» (Money) и в завершении для получения метода 9М добавляется фактор «понедельник» (Monday). Нельзя не согласиться, что последний фактор в силу своей специфики и явно слабого отношения к производству на деле действительно может иметь определенное значение в происходящих проблемах.
В методе 5Р расслаивание происходит по следующим факторам:
1) Люди (Peoples);
2) Процедуры (Procedures);
3) Потребители или покровители (Patrons);
4) Среда (Place);
5) Ресурсы (Provisions).
Все рассмотренные методы можно с успехом применять при построении гистограмм, диаграмм Парето и Исикавы, при разработке контрольных листков. При этом необязательно строго использовать конкретный метод, ведь цель всех приведенных методов состоит в том, чтобы помочь выделить основные факторы и исследователь может использовать методы частично, добавляя собственноручно установленные или известные факторы к рекомендуемым стандартным.
Следует заметить, что методика 9М ввиду своей громоздкости крайне редко используется в чистом виде. Наиболее оптимальным является подход, состоящий в выборе необходимых факторов из предлагаемого методом многообразия.
Анализ производственных процессов. Оценка стабильности и качества
В предыдущих разделах мы рассматривали инструменты, позволяющие:
- выявить главные направления работ по улучшению качества;
- установить причины и факторы, влияющие на неудовлетворительные значения показателей, характеристик;
- проследить связь между причиной результатом.
Но все это возможно только тогда, когда мы располагаем фактами о том, что у исследуемого нами процесса есть проблемы. Доктор Ллойд Нильсон, - руководитель отдела статистических методов в "Nasyua Corporation" писал: «К сожалению, наиболее важные факторы, необходимые для управления любой организацией, как правило, неизвестны и количественно не определены».
Все рассмотренные нами методы в основном работают уже с данными о браке. Обнаружение брака и его анализ, конечно же, важные направления деятельности любой организации. Разрабатываемые в дальнейшем корректирующие действия устраняют причины несоответствий, что, безусловно, положительным образом сказывается на качестве процессов и продукции. Однако, бороться с проблемами лишь по мере их возникновения не самый лучший вариант если речь идет о продукции, услугах, производственных процессах, ведь все это приводит к значительным затратам и по сути от будущего брака, вызванного иными причинами не спасает.
Наиболее эффективной является стратегия предупреждения брака. Для ее реализации необходимо периодически собирать данные о функционировании процесса и применять различные статистические методы, такие, например как гистограммы, контрольные карты, анализ пригодности и воспроизводимости.
Перечисленные методы позволяют предсказывать поведение процесса и своевременно вносить требуемые корректировки с целью недопущения брака и непрерывного совершенствования.
Гистограммы
Одним из самых простых применений для статистических данных собранных о процессе может быть построение гистограммы.
Гистограмма представляет собой столбиковую диаграмму, посредством которой можно изучать распределение исследуемого параметра или процесса в целом.
Алгоритм построения гистограммы приведен на рисунке 3.1. В соответствии с данным алгоритмом можно выделить восемь этапов построения гистограммы:
1) Сбор статистических данных.
На данном этапе следует собрать необходимое количество статистических данных об объекте исследования. Для удобства дальнейшей обработки информации при сборе данных весьма удобно использование предварительно разработанного контрольного листка.
Следует заметить, что чем большее количество данных будет собрано, тем более достоверной будет построенная гистограмма, и тем больше информации мы получим об изучаемом процессе. Конечно же большой объем данных более сложен в обработке, однако применение соответствующих программных средств полностью решает эту проблему.
Стоит также сказать о минимальном объеме данных. Строгих требований к нему не установлено, однако руководствуясь здравым смыслом можно утверждать, что построение гистограммы по 10 или 20 значениям не даст представления о распределении исследуемого параметра процесса и является нецелесообразным. Гистограмма же построенная по 50 значениям будет вполне информативной.
2) Определение минимального и максимального значений.
Если для сбора данных применялся контрольный листок, то информацию о минимальном (xmin) и максимальном (xmax) значении выборки можно извлечь непосредственно из него.
3) Вычисление размаха.
Выборочный размах (R) вычисляется как разность между максимальным и минимальным значением выборки, определенными на предыдущем этапе, т.е.:
R= xmax –xmin.

Рис. 3.1.Алгоритм построения гистограммы
4) Определение количества и ширины классов (интервалов).
Число интервалов (k) можно определить несколькими способами:
а) по формуле Старджесса:
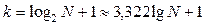 ,
,
где N – объем выборки.
б) по формуле Брукса и Каррузера:
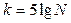 .
.
в) из соотношения:
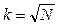 .
.
Все приведенные формулы в подавляющем большинстве случаев в результате дают дробное число. При этом часто возникает неопределенность, выбрать большее или меньшее число интервалов. Можно придерживаться следующей рекомендации: при числе значений от 100 и выше следует выбирать более узкий интервал (т.е. число интервалов следует округлять в большую сторону), а при числе значений менее 100 выбирают более широкий интервал (т.е. число интервалов следует округлять в меньшую сторону).
Ширина интервала (h) при этом определяется по формуле:
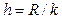 .
.
При вычислениях по данной формуле ширина интервала обычно является дробным числом с большим или бесконечным числом знаков после запятой и требует округления. Округление следует проводить в большую сторону, так как в противном случае последний интервал не охватит максимальное значение выборки.
Существует еще один подход к определению числа классов и ширины интервала, являющийся по сути обратным к вышеописанному. Суть подхода состоит в том, что сначала выбирается ширина класса из ряда чисел (1; 2; 2,5; 4; 5)∙10n, где n – целое положительное или отрицательное число. Подобная величина ширины интервала упрощает построение гистограммы и делает граничные значения классов более удобными для восприятия.
Далее определяется количество классов (интервалов) из соотношения:
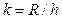 .
.
Полученное значение обычно округляется в большую сторону, с тем, чтобы оба граничных значения выборки попали диапазон построения гистограммы.
При использовании данного подхода число интервалов будет различным, в зависимости от того какой шаг был выбран изначально. Для одной и той же выборке при разном шаге число интервалов может быть равно и 4 и 20. Оптимальную величину шага следует выбирать исходя из числа получаемых классов с учетом следующих рекомендаций: при количестве наблюдений 25…40 – 5…6 классов, при количестве наблюдений 40…60 – 6…8 классов, 60…100 – 7…10, 100…200 наблюдений – 10…12, более 200 наблюдений – 12…15 классов.
5) Определение границ классов (интервалов).
Границы интервалов следует определять так, чтобы они включали наименьшее и наибольшее значение выборки. Т.е. нижняя граница первого интервала, должна быть немного меньше минимального значения, а граница последнего немного больше максимального значения выборки.
Определив нижнюю границу первого интервала, прибавляем к ней ширину класса и получаем границу между первым и вторым классом. Продолжая далее прибавлять к граничным значениям величину ширины интервала можно рассчитать границы всех классов. При этом следует убедиться, что максимальное значение выборки попало в последний интервал.
6) Вычисление частот.
На данном этапе требуется подсчитать число значений, попадающих в каждый интервал (fi).
При использовании контрольного листка для решения данной задачи следует суммировать частоты для соответствующих значений, попадающих в интервал.
Если сбор данных осуществлялся без использования контрольного листка, то для упрощения вычисления частот выборку стоит преобразовать в вариационный ряд (ряд значений, расположенных по возрастанию).
Также следует вычислить относительные частоты (pi) по формуле:
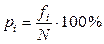 ,
,
где fi – абсолютная частота для i-го класса;
N – объем выборки.
Достаточно часто может произойти ситуация, когда какие-либо значения выборки попадают на границы интервалов. В этом случае правую границу класса следует считать началом следующего интервала и соответствующие значения относить к последующему интервалу. Исключение составляет последний класс, в котором правое граничное значение следует относить к этому же интервалу.
7) Построение столбиковой диаграммы.
Для ее построения на лист наносятся две вертикальные оси и одна горизонтальная. На левой вертикальной оси откладываются значения частот, а на правую – значения относительных частот. Горизонтальная ось характеризует величину контролируемого параметра.
Далее следует определиться с масштабом и разметить соответствующие оси. После чего на горизонтальную ось наносятся границы классов, при этом не рекомендуется отмечать классы непосредственно от вертикальной оси. Для наглядности следует отступить от нее на величину одного-двух интервалов. Аналогичной рекомендации следует придерживаться и к расположению последнего класса относительно правой вертикальной оси.
На отрезках, соответствующих классам, строим прямоугольники, высоты которых равны частоте, вычисленной для каждого интервала.
В итоге получаем столбиковую диаграмму, именуемую гистограммой.
8) Нанесение линий номинала, границ допуска и среднего арифметического.
Для расширения возможностей анализа гистограммы на нее наносят имеющуюся информацию о процессе, в частности линии номинального значения, границ допуска, среднего арифметического. Также можно нанести линии, соответствующие трем стандартным отклонениям.
Для большей информативности гистограмму можно дополнить текстовыми данными о наименовании процесса или продукции, периоде сбора статистических данных, дате построения, объеме выборки, среднем и номинальном значении, границах допуска.
После того как гистограмма построена можно приступать к ее анализу. Здесь многое о процессе можно узнать уже по форме гистограммы. Выделяют следующие основные типа гистограмм (рисунок 3.2):
1) Колоколообразное распределение.
Данное распределение характеризуется симметричной формой и максимумом обычно на центральном интервале. Визуально форма гистограммы напоминает закон нормального распределения. Подобная форма графика встречается наиболее часто, соответствует большинству производственных процессов и свидетельствует об их нормальном течении. Отклонения от колоколообразной формы могут свидетельствовать о наличии каких-либо воздействующих факторов.
2) Распределение гребенчатого типа.
Распределениям подобного типа характерно чередование высоких и низких столбиков. Подобная ситуация указывает на возможные повторяющиеся ошибки измерений или применение определенных правил округления данных. Также подобная картина могла получиться при неверной группировке данных по классам. В этом случае следует проверить данные или выбрать другое число классов.
3) Положительно (отрицательно) скошенное распределение.
Пик распределения смещен от центра либо в левую, либо в правую сторону. Со стороны, к которой смещен пик распределение более обрывисто чем с противоположной.
Распределение в котором пик смещен влево, а правая сторона плавно снижается в направлении увеличения параметра называется положительно скошенным. Распределение в котором пик смещен вправо, а левая сторона плавно снижается в направлении уменьшения параметра называется отрицательно скошенным.
Несмотря на некоторое сходство с нормальным, скошенное распределение таковым не является, и получение подобных гистограмм указывает на следующие ситуации:
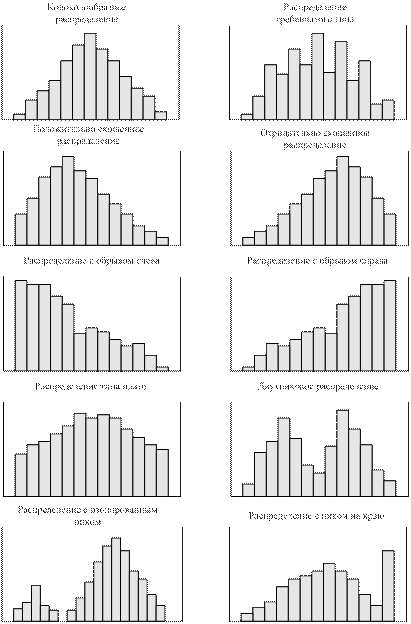
Рис. 3.2.Основные типы гистограмм
а) Производственный процесс не позволяет получить значения больше или меньше определенной величины, либо в случае отсутствия такой необходимости. Подобная ситуация часто возникает при одностороннем задании требований к параметрам, в частности, например, величина допустимой шероховатости задается лишь максимальным значением. Если рассматривать образовательный процесс, то при написании теста студент не может получить оценку выше 100% и в подобной ситуации, при хорошем уровне подготовки обучаемых, скорее всего будет иметь место отрицательно скошенное распределение.
б) На процесс оказывает влияние фактор, вызывающий смещение среднего значения процесса или увеличивающего размах параметра. Одной из причин может быть износ инструмента или оснастки.
4) Распределение с обрывом слева (справа).
Распределению данного типа свойственно расположение пика либо в левом или правом краю, либо в непосредственной близости от низ, т.е. распределение имеет ассиметричную форму. При этом на стороне, к которой смещен пик, имеется обрыв данных, в то время как другая сторона имеет плавный спад столбцов как у гистограммы колоколообразного типа.
Гистограмма подобного типа может получиться после процедуры сплошного контроля, в случае наличия большого числа бракованных изделий, т.е. столбцы, соответствующие браку, с той или другой стороны были отсечены.
5) Распределение типа плато.
При данном распределении наблюдается относительно равномерное распределение частот в классах. Частоты столбцов центральных классов не намного отличаются от крайних. Данный вид распределения также называют равномерным или прямоугольным.
Подобную картину можно наблюдать когда итоговая выборка была по сути составлена из нескольких, которые имеют отличающиеся в пределах поля допуска средние значения. Например, это могут выборки, взятые с разных станков, или детали, изготовленные разными рабочими. Для получения более достоверной информации о процессе в подобных ситуациях необходимо прибегнуть к стратификации данных.
6) Двухпиковое распределение.
Исходя из названия в данном распределении присутствую два расположенные на удалении друг от друга пика, между которыми наблюдаются классы с более низкими частотами.
Данная ситуация получается при объединении двух выборок с различными средними значениями. Как и в предыдущем случае для дальнейшего анализа процесса необходимо прибегнуть к стратификации данных.
7) Распределение с изолированным пиком.
Данное распределение имеет сходство с предыдущим. Однако если в предыдущем случае оба распределения имели примерно одинаковый объем данных, то в данном случае второе распределение весьма незначительно.
Причиной получения подобной гистограммы могут быть включение в выборку небольшого количества данных из другого распределения, либо изредка происходящие сбои производственного процесса, требующие выявления и изучения. Также малое распределение может быть следствием периодических одинаковых ошибок измерений или попросту опечаток.
8) Распределение с пиком на краю.
Данное распределение имеет значительный пик, расположенный слева или справа от основного распределения. Подобная ситуация могла возникнуть в случае объединения всех значений, лежащих ниже или выше определенного числа в один класс.
Все описанные выше ситуации предполагают изучение процесса только на основе визуального представления распределения данных, однако более детально можно изучить процесс, нанеся на гистограмму в частности границы поля допуска, среднее арифметическое и т.д. Подробно эти моменты будут рассмотрены в разделе 3.3.
Пример. Необходимо проанализировать с помощью гистограммы процесс изготовления валика, на основе контрольного листка, приведенного на рис. 1.1.
Первый этап алгоритма построения гистограммы (сбор статистических данных) в нашем случае уже выполнен, так имеется заполненный контрольный листок.
Далее исходя из него определяем минимальное и максимальное значения:
xmin=10,292 мм; xmax=10,311 мм.
Теперь можно переходить к следующему этапу – вычислению размаха:
R= xmax –xmin.=10,311-10,292=0,019 мм.
Для определения количества и ширины классов воспользуемся вторым подходом, т.е. сначала зададимся шагом. Выбирать будем из следующих вариантов: 0,002 мм; 0,0025 мм; 0,004 мм. Варианты шага 0,001 мм и 0,005 мм не рассматриваем, так как в первом случая уже изначально очевидно, что мы получим слишком большое число классов, а втором наоборот, их будет явно недостаточно.
Итак, вычислим ширины классов:
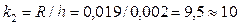 ;
;
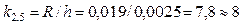 ;
;
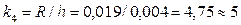 .
.
Учитывая объем выборки N=158, принимаем решение, что для данного случая оптимально число классов k=10 и шаг h=0,002 мм.
Так как для построения гистограммы рекомендовано границы крайних интервалов устанавливать за пределы граничных значений, то левую границу первого класса установим равной 10,2915 мм. От данного значения и будем откладывать интервалы.
Для удобства построения гистограммы воспользуемся таблицей, в которую будем вносить всю необходимую информацию, такую как границы классов, абсолютные и относительные частоты (табл. 3.1).
Так как в качестве начального значения было выбрано 10,2915 мм, то для получения верхней границы первого класса к нему прибавляем величину шага, т.е.:
10,2915+0,002=10,2935 мм.
Итак, нижняя граница первого класса 10,2915 мм, а верхняя 10,2935 мм. Верхняя граница первого класса будет являться нижней границей для второго класса, при этом его верхнюю границу можно определить также, как и для первого класса. Аналогично вычисляем границы всех классов и заносим их в табл. 3.1.
Для определения абсолютных частот, воспользуемся контрольным листком (рис. 1.1). В первый класс попадают два значения 10,292 мм и 10,293 мм. Общее количество изделий, соответствующих данным результатам измерений равно 4. Аналогично, во второй класс попадают результаты измерений 10,294 и 10,295 мм, к ним относятся 12 измерений. Аналогично определяем частоты для всех классов и заносим их в табл. 3.1.
Относительные частоты определяем как отношение абсолютной частоты в каждом классе к числу проконтролированных изделий N=158 умноженное на 100%. Для первого класса относительная частота будет равна:
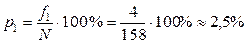 .
.
Аналогично вычисляем относительные частоты для остальных классов и заносим их в табл. 3.1.
Т а б л и ц а 3.1. Таблица для построения гистограммы
| № класса | Границы класса, мм | Абсолютная частота, шт. | Относительная частота, % |
| 10,2915…10,2935 | 2,5 | ||
| 10,2935…10,2955 | 7,6 | ||
| 10,2955…10,2975 | 13,3 | ||
| 10,2975…10,2995 | 18,3 | ||
| 10,2995…10,3015 | 20,3 | ||
| 10,3015…10,3035 | 15,8 | ||
| 10,3035…10,3055 | 11,4 | ||
| 10,3055…10,3075 | 5,7 | ||
| 10,3075…10,3095 | 3,2 | ||
| 10,3095…10,3115 | 1,9 | ||
| Итого |
После заполнения табл. 3.1 можно приступать к построению гистограммы. Шаг по левой вертикальной оси, соответствующей абсолютным частотам выбираем равным 5, а по правой, соответствующей относительным частотам равным 3. На горизонтальной оси откладываем значения, соответствующие границам интервалов, крайние значения при этом отмечаем на некотором расстоянии от вертикальных осей. Далее строим столбиковую гистограмму. Высота столбца на каждом интервале соответствует частоте попадания диаметра валика в соответствующий класс (табл. 3.1). В итоге выполнения описанных мероприятий получаем гистограмму, представленную на рис. 3.3.
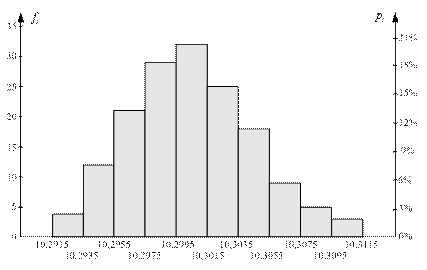
Рис. 3.3.Гистограмма
Прежде чем перейти к последнему этапу построения, проанализируем полученный результат. Визуально распределение данных на гистограмме соответствует колоколообразному (нормальному распределению), однако имеет незначительную асимметрию, несмотря на это можно сделать предварительный вывод о нормальном течении процесса производства валиков. Тем не менее, руководствуясь исключительно визуальным сходством, нельзя утверждать о соответствии наблюдаемого распределения нормальному, т.е. необходимо подтверждение с помощью статистических гипотез, которое будет рассмотрено в разделе….
Теперь нанесем на гистограмму линии номинального значения, среднего арифметического и пределов допусков. В итоге получим гистограмму, представленную на рис. 3.4.
Внесенная на график информация дает более полное представление о процессе. В частности мы видим тот факт, что имеет место бракованная продукция. Об этом свидетельствуют столбцы, превышающие верхнюю границу допуска. При этом, как уже было отмечено выше, гистограмма асимметрична и вытянута вправо. Решение данной проблемы позволит сократить размах в диаметрах изготавливаемых валиков и тем самым снизить уровень брака.
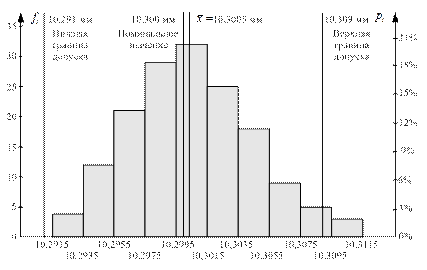
Рис. 3.4.Гистограмма с дополнительной информацией
С левой стороны мы наблюдаем небольшой запас по допуску, что с одной стороны является хорошим признаком. С другой стороны следует принять во внимание смещение среднего значения процесс вправо, которое необходимо минимизировать или устранить. В свою очередь устранение этого смещения сдвинет гистограмму влево и практически вплотную приблизит ее к границе допуска, а учитывая тот факт, что любой процесс в той ли иной степени подвержен изменчивости, то велика вероятность появления изделий, параметр которых выйдет за нижнюю границу допуска.
Таким образом, можно сделать вывод о неудовлетворительном состоянии процесса, он нуждается в мерах по снижению изменчивости, настройке на номинал и устранению причин асимметрии.
Контрольные карты
Как мы уже выяснили в предыдущем разделе, гистограммы позволяют выявлять явные отклонения в производственном процессе и своевременно предпринимать корректирующие действия. Тем не менее, даже если у нас получилась гистограмма с колоколообразным (нормальным) распределением и даже если размещается внутри поля допуска, это далеко не всегда означает, что у исследуемого процесса нет проблем и что завтра, взяв выборку, мы сможем получить аналогичный результат.
Гистограммы не позволяют оценивать стабильность и управляемость процесса. Конечно, можно попробовать предложить строить гистограммы периодически и наблюдая за динамикой ее изменения пытаться делать вывод о стабильности, однако подобные выводы будут основаны исключительно на глазомерной информации и к тому же окажутся весьма субъективными.
Для принятия более обоснованного решения о стабильности процесса необходим объективный инструмент статистического контроля. Таким инструментом являются контрольные карты.
Они были разработаны в 20-х годах прошлого века доктором Уолтером Шухартом, работавшим в то время в Bell Telephone Laboratories. Целью разработки было создание инструмента, способного выявлять особые, неслучайные изменчивости в процессе. Контрольные карты являются простым, но в тоже время очень мощным средством контроля процесса и однозначно указывают на особые причины изменчивости.
По сути, контрольная карта является разновидностью графика (рис. 3.5), который отражает динамику изменчивости процесса, т.е. изменение показателей качества во времени. На контрольной карте имеется три линии:
1) UCL (Upper control limit) – верхняя контрольная граница;
2) CL (Center line) – центральная линия;
3) LCL (Lower control limit) – нижняя контрольная граница;
Выход какой-либо точки за контрольные границы является одним из основных признаков выхода процесса из стабильного, управляемого состояния.
Построение контрольных карт преследует следующие основные цели:
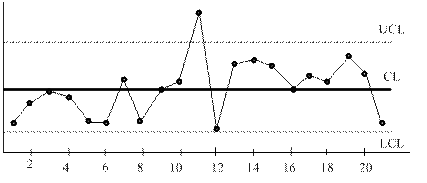
Рис. 3.5.Контрольная карта Шухарта
1) Наглядно представить динамику поведения процесса;
2) Контролировать значение определенной характеристики;
3) Проверять стабильность и управляемость процессов;
4) Принимать корректирующие меры;
5) Проверять эффективность принятых мер.
Как достичь перечисленных целей будет рассмотрено позже.
Все контрольные карты делят на две большие группы:
1) Контрольные карты по количественному признаку;
2) Контрольные карты по альтернативному признаку.
Контрольные карты по количественному признаку применяются для процессов, в которых можно измерить тот или иной параметр. В качестве параметров могут выступать габаритные размеры, масса, сопротивление, усилие, время и т.д. Они являются наиболее часто применяемыми, ведь практически у каждого процесса можно измерить ту или иную характеристику. К тому же количественные измерения дают большой объем информации об исследуемом процессе.
Выделяют следующие разновидности контрольных карт по количественному признаку:
1) 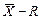 – контрольная карта (карта средних значений и размахов);
– контрольная карта (карта средних значений и размахов);
2) 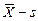 – контрольная карта (карта средних значений и стандартных отклонений);
– контрольная карта (карта средних значений и стандартных отклонений);
3) 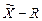 – контрольная карта (карта медиан и размахов);
– контрольная карта (карта медиан и размахов);
4) 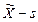 – контрольная карта (карта медиан и стандартных отклонений);
– контрольная карта (карта медиан и стандартных отклонений);
5) 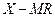 – контрольная карта (карта индивидуальных значений и скользящих размахов);
– контрольная карта (карта индивидуальных значений и скользящих размахов);
6) CuSum – контрольная карта (карта кумулятивных сумм).
Контрольные карты по альтернативному признаку применяются в случае, когда в распоряжении исследователя имеются данные не о значениях характеристик, а, например, о фактах соответствия или несоответствия требованиям. Примером таких данных могут быть результаты контроля гладкими калибрами, т.е. когда мы не измеряем диаметр отверстия или вала, а лишь проверяем факт годности изделия. Другим примером может служить число дефектов на изделии, число ошибок в документе.
Данные для построения контрольных карт по альтернативному признаку можно получить для большинства процессов, причем порой с меньшими затратами по сравнению с количественной информацией.
Выделяют следующие разновидности контрольных карт по альтернативному признаку:
1) 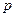 – контрольная карта (карта доли несоответствующих единиц продукции);
– контрольная карта (карта доли несоответствующих единиц продукции);
2) 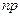 – контрольная карта (карта числа несоответствующих единиц продукции);
– контрольная карта (карта числа несоответствующих единиц продукции);
3) 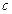 – контрольная карта (карта числа несоответствий);
– контрольная карта (карта числа несоответствий);
4) 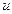 – контрольная карта (карта числа несоответствий на единицу продукции).
– контрольная карта (карта числа несоответствий на единицу продукции).
Следует заметить, что для некоторых процессов бывает целесообразно анализировать одновременно контрольные карты из обоих групп, при наличии соответствующих данных.
Несмотря на большое разнообразие контрольных карт, алгоритм их построения аналогичен и представлен на рис. 3.6.
Рассмотрим этапы построения контрольной карты:
1) Планирование сбора данных.
На данном этапе необходимо определить порядок и периодичность сбора данных, а также их планируемый объем. Общий период сбора данных не должен быть слишком длительным. Ведь если этот период будет равен месяцу, то весьма неприятно будет узнать, что мы весь месяц работали с нестабильным и неуправляемым процессом. К тому же за длительный период на процесс может успеть повлиять несколько негативных факторов и в этом случае задача по их выявлению значительно усложнится.

Рис. 3.6.Алгоритм построения контрольной карты
Периодичность сбора данных зависит от общего периода исследования. Если, например, он составляет одни сутки, то данные можно собирать каждые полчаса или час.
Объем данных во много зависит от типа контрольной карты. Для карт по количественному признаку бывает достаточно проконтролировать порядка 100 единиц продукции. Исключение составляют карты индивидуальных значений и скользящего размаха, где объем выборки гораздо меньший. Для карт по альтернативному признаку объем исследуемых образов требуется гораздо больший, ведь необходимо учитывать продукцию с дефектами, а ее в большинстве случаев не так и много. Следовательно, объем контролируемой продукции может составлять сотни, а иногда и тысячи единиц.
Для построения любых контрольных карт, за исключением карт индивидуальных значений и скользящего размаха, необходима группировка данных. Она по большей части связана с периодичностью сбора информации. В каждый период контролируется группа продукции определенного объема. При этом объем такой группы желательно должен быть одинаковым и зависит он от типа контрольной карты. Для карт по количественному признаку объем группы в большинстве случаев составляет 4-5 единиц, но допускаются и другие объемы. Для карт по альтернативному признаку объем подгрупп может составлять от десятков до сотен единиц продукции.
2) Сбор статистических данных.
После того как мы определились с объемом и периодичностью сбора данных непосредственно приступают к данному процессу. Особое внимание следует уделить записи данных. Если, например, для построения гистограммы порядок записи результатов контроля абсолютно не важен, то для контрольных карт он имеет первостепенное значение, так как одна из целей их построения – отслеживание динамики изменения процесса во времени.
3) Вычисление точек контрольной карты.
На каждую контрольную карту наносятся точки, получаемые расчетным путем из сгруппированных исходных данных. Формулы для расчета точек будут приведены в последующих разделах.
4) Определение центральной линии.
В большинстве случаев значение центральной линии определяется как среднее арифметическое всех точек. Конкретные формулы будут приведены в последующих разделах.
5) Определение контрольных границ.
Контрольные границы определяются расчетным путем с использованием значения центральной линии. Для каждой контрольной карты расчетные формулы индивидуальны и будут приведены в последующих разделах.
6) Нанесение полученной информации на бланк контрольной карты.
При неавтоматизированном способе построения контрольной карты удобно использовать заранее подготовленные бланки (рис. 3.7 и рис. 3.8).
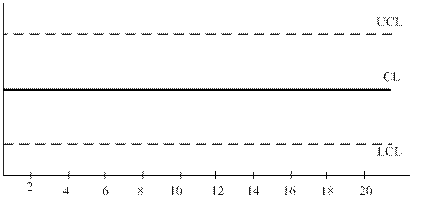
Рис. 3.7.Бланк для построения контрольной карты с симметричными контрольными границами
Рис. 3.8.Бланк для построения контрольной карты с несимметричными контрольными границами
На бланки необходимо заранее нанести центральную линию, линии контрольных границ и по горизонтальной оси сделать разметку для подгрупп. На бланки для контрольных карт с несимметричными контрольными границами (например, R-карта) нижняя граница не наносится, так как заранее неизвестно ее относительное расположение.
Итак, для построения контрольной карты с использованием бланка сначала необходимо произвести разметку вертикальной оси и указать значения центральной линии и контрольных границ. Для контрольной карты с несимметричными границами, нижняя контрольная граница наносится после разметки вертикальной оси.
Далее над соответствующими отметками на горизонтальной оси наносятся точки, которые в дальнейшем соединяются линией. Полученный график и будет называться контрольной картой.
Дальнейшая работа с контрольной картой состоит в ее анализе.
Явным признаком того, что процесс перестал быть стабильным (управляемым) является выход хотя бы одной точки за контрольные границы. Это означает, что на процесс влияют не только обычные (случайные) факторы, но и в определенный момент он стал подвержен влиянию некого определенного фактора. Влияние подобных факторов может быть различной длительности. Оно может выражаться в разовом проявлении, а может продолжаться и в дальнейшем. Вне зависимости от длительности влияния фактора, необходимо его выявить и предпринять действия по его устранению и исключению дальнейшего появления.
Сигналом о выходе процесса из стабильного состояния, могут также являться серии точек, особым образом расположенные на контрольных картах. Для проведения подобного анализа контрольная карта делится на зоны – A, B и C (рис. 3.9).
Как правило зона А определяется как область, расположенная на расстоянии от 2 до 3 стандартных отклонений по обе стороны от центральной линии. Зона В определяется как область, отстоящая от центральной линии на расстояние от 1 до 2 стандартных отклонений, а зона С - как область, расположенная между центральной линией по обе ее стороны и ограниче
