Системы счисления, используемые в ЭВМ
Для изображения чисел используются определенные приемы и правила, называемые системами счисления. Все известные системы счисления делятся на две группы: позиционные системы счисления и непозиционные системы счисления.
Непозиционной системой счисления называется такая система, в которой значение символа, цифры, знака или иероглифа не зависит от позиции этого символа в изображаемом числе. В позиционных системах наоборот, значение символа зависит от позиции этого символа в изображаемом числе. Непозиционные системы, как более простые, появились исторически гораздо более раньше позиционных систем. Ими пользовались древние славяне, китайцы и другие народы.
До наших дней дошла одна из разновидностей непозиционных систем - римская система счисления. В ней используются так называемые римские цифры: I- 1, V- 5, X- 10, L- 50, C- 100, D- 500, M- 1000. Значение числа вычисляется суммированием всех чисел с учетом правила, что если цифра меньшего веса стоит слева от следующей за ней цифрой большего веса, то она имеет знак минус, а если справа - то знак плюс. Например, число MCCXXXIV определяется следующим образом:
1000 + 100 + 100 + 10 + 10 + 10 - 1 + 5 = 1234
Непозиционные системы счисления обладают двумя существенными недостатками. Во-первых, при увеличении диапазона представленных чисел увеличивается число различных символов в изображаемых числах. Во-вторых, очень сложны правила выполнения даже самых простых арифметических действий.
Позиционные системы счисления обладают тем чрезвычайно важным свойством, что все числа, и малые, и большие, могут быть записаны с помощью конечного набора различных символов. Кроме того, правила действия с числами могут быть резюмированы в виде таблиц сложения и умножения. Изобретение позиционных систем счисления имело неоценимые последствия для дальнейшего развития человеческой цивилизации. Впервые такие системы счисления стали использовать древние шумерийцы и индусы.
В позиционных системах счисления любое число X изображается в виде полинома
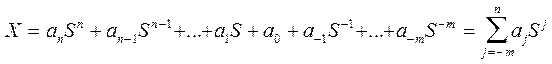. (4.1)
B этом выражении ajназываются коэффициентами, а S - основанием системы счисления. Значение любого коэффициента в изображаемом числе может лежать в диапазоне 0...(S-1). В настоящее время во всех странах мира используется десятичная система счисления, представляющая собой позиционную систему счисления с основанием S=10. Коэффициенты при изображении чисел в десятичной системе счисления могут принимать значения в диапазоне от 0....9. Для краткости вместо записи числа в виде полинома записывают только последовательность коэффициентов этого полинома. Когда мы пишем десятичное число X=94,46 , то подразумеваем величину
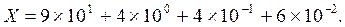
Значение первой цифры слева от запятой, отделяющей целую часть числа от его дробной части, соответствует значению изображенной цифры (говорят, что ее “вес” равен единице); значение следующей цифры слева равно десятикратному значению изображаемой цифры (“вес” цифры - 10) и т.д. Значение цифры справа от запятой равняется десятой части написанной цифры, (ее “вес” равен 0,1) следующей - сотой части и т. д.
В принципе, роль основания способно играть любое целое число, большее единицы. Возьмем, например, десятичное число 437. Вполне возможно записать это число и как
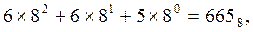
где индекс 8 у числа 665 указывает, что мы имеем дело с числом, при записи которого вместо обычного основания S=10 используется основание S=8. Числа, записанные в системе счисления с основанием 8, называются восьмеричными.
То же самое десятичное число 437 можно записать в виде
.
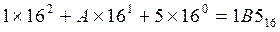Числа, записанные в системе счисления с основанием 16, называются шестнадцатеричными (А соответствует цифре 10 в десятичной системе).
Простейшей позиционной системой счисления является система с основанием S=2. В этой системе число
.
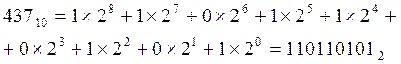Преимущество использования двойки в качестве основания системы счисления состоит в том, что требуются только две различные цифры для записи любого числа - 0 и 1. Недостаток двоичной системы в том, что для изображения числа в двоичной форме требуется примерно в 3,3 раза больше цифр, чем в десятичной.
Подобно тому, как для записи десятичных чисел используют десять различных цифр (09), для написания двоичных чисел применяют две различные цифры (0 и 1), восьмеричных - восемь (07) и шестнадцатеричных - 16. Так как только десять цифр из шестнадцати имеют общепринятые обозначения арабскими цифрами 09, то для записи остальных цифр 1015 шестнадцатеричных чисел используют символы латинского алфавита AF (A соответствует цифре 10, В- 11, C- 12, D- 13, E- 14, F- 15). Так, например, шестнадцатеричное число 2Е соответствует десятичному числу 46, так как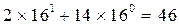 
.
С дробными числами при любом основании обращаются так же, как и в десятичной системе. Необходимо лишь учитывать то обстоятельство что конечная дробь в одной системе счисления может стать периодической в другой. Так, например,
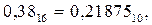но 
.
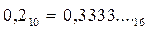В ЭВМ используются позиционные системы счисления с основаниями 2, 8, 16, 10. Основной системой счисления является двоичная. Во-первых, в этой системе счисления, как уже говорилось, для изображения чисел необходимы только комбинации двух цифр: 0 и 1. Эти две цифры можно изображать элементами, имеющими два различных состояния. Одному состоянию, причем любому, можно поставить в соответствие цифру 0, а другому - 1. Такие элементы называются двухпозиционными (две позиции - два состояния) и они исключительно легко изготавливаются технически.
Для сравнения укажем, что для изображения одной десятичной цифры необходимо иметь элемент, имеющий 10 четко выраженных различных состояний. В принципе, логика выполнения арифметических операций в двоичной системе счисления наиболее проста. Это наглядно на примере сравнения таблиц умножения десятичных цифр с одной единственной таблицей умножения двоичных цифр имеющей вид:
00=0; 01=0; 10=0; 11=1.
Из приведенных примеров видно, что десятичная система счисления крайне неудобна для использования в ЭВМ, но она общепринята, и поэтому, не смотря на свои недостатки, так же нашла применение в вычислительной технике. Для того чтобы ввести в ЭВМ десятичные числа, отобразить их состояниями двухпозиционных элементов, используется так называемая двоично-десятичная форма представления десятичных чисел. В этой форме каждая цифра десятичной записи числа изображается в виде четырехразрядного двоичного числа (двоичной тетрады). Например, десятичное число X10=481,75 в двоично-десятичной форме будет иметь вид:
4 8 1, 7 5
X2-10=0100 1000 0001, 0111 0101.
Нельзя путать двоично-десятичную форму записи числа с двоичной записью того же числа! В первом случае основание системы счисления остается равным десяти - только коэффициенты при основании выражены в двоичной форме.
Восьмеричная и шестнадцатеричная форма записи в основном используются при программировании задач для ЭВМ и введения компактных записей во время отладки программ. Достоинства этих форм записи числа - легкость перевода из двоичной формы в восьмеричную (шестнадцатеричную) и наоборот, с одной стороны, и компактность изображения чисел, с другой стороны. Например, чтобы перевести шестнадцатеричное число X16=1FA,0F в двоичную форму, необходимо каждую шестнадцатиричную цифру представить эквивалентным четырехразрядным двоичным числом. В итоге получим:
7 F В, 0 Е
0111 1111 1011, 0000 1110.
Аналогично для восьмеричного 34:
5 6
101 110.
В таблице 4.1 приведены различные формы записи двадцати чисел натурального ряда.
Таблица 4.1. Различные формы записи двадцати чисел натурального ряда
| Десятичное число | Двоичное число | Восьмеричное число | Шестнадцати-ричное число | Двоично-десятичное число |
| A | 0001 0000 | |||
| B | 0001 0001 | |||
| C | 0001 0010 | |||
| D | 0001 0011 | |||
| E | 0001 0100 | |||
| F | 0001 0101 | |||
| 0001 0110 | ||||
| 0001 0111 | ||||
| 0001 1000 | ||||
| 0001 1001 | ||||
| 0010 0000 |
Необходимо особо подчеркнуть:
1. Количество, которое отражает цифровая запись числа остается неизменным, независимо от системы счисления;
2. Правила выполнения арифметических операций над многоразрядными числами представленными в позиционных системах счисления с различными основаниями, одни и те же.
3. Правила сложения и умножения одноразрядных чисел для каждой системы счисления определяются своими таблицами умножения и сложения.
Рассмотрим пример. Пусть нам необходимо найти произведение двух восьмеричных чисел: X8=35´12 (эти числа соответствует десятичным 29 и 10 соответственно).
Будем умножать “столбиком”:
 |
Ответ: X8=4314=644=6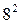 
+4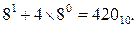 
Умножая 4 на 3 в восьмеричной системе, получаем результат 148 (это соответствует 12 в десятичной системе). Следовательно, согласно правилам, в данном разряде записывается число 4, а единица переноса запоминается. Умножая далее 4 на 4 получаем 20 в восьмеричной ситсеме, а с учетом единицы переноса - цифру 21. Таким образом, результатом умножения восьмеричного числа 43 на цифру 4 будет восьмеричное число 214. Аналогично умножается множимое 43 на следующую цифру множителя 431=43. При сложении полученных таким образам частичных сумм необходимо пользоваться соответствующими таблицами сложения. Окончательный ответ в восьмеричной форме 644 соответствует десятичному числу 420.
Порядок вычислений на ЭВМ обычно таков. Исходные числовые данные вводятся в ЭВМ в обычной для человека десятичной форме (например, с помощью клавиатуры - устройства ввода). ЭВМ имеют в своем составе специальные устройства, называемые шифраторами, которые осуществляют автоматический перевод вводимой десятичной информации в двоично-десятичную форму. По специальной подпрограмме или схеме (разработаны специальные большие интегральные схемы, осуществляющие автоматический перевод чисел из двоично-десятичной записи в двоичную запись и наоборот) числовая информация из двоично-десятичной формы переводится в двоичную запись. Затем производятся необходимые вычисления в двоичной системе счисления. Если необходимо выдавать какие-то результаты вычислений в десятичной форме, то эти данные, программно или с помощью специальных микросхем, переводятся сначала в двоично-десятичную форму, а затем с помощью устройств вывода выдаются непосредственно в десятичной форме (например, печатаются на бланке или высвечиваются на экране дисплея).
Такой порядок вычислений используется при решении научно-технических задач. В таких задачах количество исходных числовых данных и результатов вычислений сравнительно невелико по сравнению с количеством операций, необходимых для решения задач.
В то же время имеется достаточно большой класс задач, отличающийся обилием входных и выходных данных и требующих для своего решения небольшого числа вычислительных операций (например начисление зарплаты рабочим и служащим, расчет квартплаты). Для таких задач описанный выше порядок вычислений не является оптимальным из-за низкой производительности ЭВМ - слишком много времени она будет тратить на переводы числовой информации из двоично-десятичной формы в двоичную и наоборот. Для решения указанных задач разработаны оптимальные методы вычислений непосредственно в двоично-десятичной форме. В современных ЭВМ в системе команд обязательно присутствуют как группа команд, выполняющих операции в двоичной системе счисления (команды двоичной арифметики), так и группа команд, выполняющих операции в двоично-десятичной системе счисления (команды десятичной арифметики).