Перевод числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную

При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

a. из двоичной

101101₂=1∙2⁵+0∙2⁴+1∙2³+1∙2²+0∙2¹+1∙2⁰=32+0+8+4+0+1=44₁₀

11011101₂=1∙2⁷+1∙2⁶+0∙2⁵+1∙2⁴+1∙2³+1∙2²+0∙2¹+1∙2⁰=128+64+0+16+8+4+0+1=221₁₀

0,1101₂=1∙2^-1+1∙2^-2+0∙2^-3+1∙2^-4=0,5+0,25+0+0,0625=0,8125₁₀

b. из восьмеричной

13₈=1∙8¹+3∙8⁰=11₁₀

7145₈=7∙8³+1∙8²+4∙8¹+5∙8⁰=7∙512+64+32+5=3685₁₀

c. из шестнадцатеричной

13₁₆=1∙16¹+3∙16⁰=16+3=19₁₀

DAEF₁₆=13∙16³+10∙16²+14∙16¹+15∙16⁰=13∙4096+10∙256+14∙16+15=56047₁₀

0,D8D₁₆=13∙16^-1+8∙16^-2+13∙16^-3=13∙0,062500+8∙0,003906+13∙0,000244=0,8469200₁₀=0,84692₁₀

Перевод из двоичной системы счисления в шестнадцатеричную и обратно.

а) исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4;

б) каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с таблицей.

1. Выполнить перевод числа 10011₂ в шестнадцатеричную систему счисления

Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Имеем:

0011₂=(11₂)=3₁₆

10011₂=13₁₆

0001₂=(1₂)=1₁₆

1. Выполнить перевод числа 10110010₂ в шестнадцатеричную систему счисления

1011|0010₂

1011₂=B₁₆

10110010₂=B2₁₆

0010₂=2₁₆

1. Выполнить перевод числа 0,0010101₂ в шестнадцатеричную систему счисления

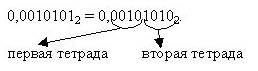
0010₂=10₂=2₁₆

0,0010101₂=0,2A₁₆

1010₂=A₁₆

Перевод из шестнадцатеричной системы счисления в двоичную:

а) каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с таблицей. Если в таблице двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады;

б) незначащие нули в результирующем числе отбрасываются.

1. Выполнить перевод числа 13₁₆ в двоичную систему счисления

1₁₆ = 1₂ = 0001₂;

3₁₆ = 11₂ = 0011₂.

13₁₆ = 0001|0011₂.

После удаления незначащих нулей имеем 13₁₆ = 10011₂

1. Выполнить перевод числа AC₁₆ в двоичную систему счисления

A₁₆=1010₂

C₁₆=1100₂

1010|1100₂

AC₁₆=10101100₂

1. Выполнить перевод числа 0,2A₁₆ в двоичную систему счисления

2₁₆=0010₂

0,2А₁₆=0,00101010₂

А₁₆=1010₂.

Отбросим в результате незначащий ноль и получим окончательный ответ: 0,2А₁₆ = 0,0010101₂

Перевод из двоичной системы счисления в восьмеричную и обратно.

Аналогично переводу из двоичной системы счисления в шестнадцатеричную. Главным отличием является то, что основанием будет 8, а не 16, и деление числа производится не тетрадами, а группами по три числа.

1. Выполнить перевод числа 10011₂ в восьмеричную систему счисления

10|011₂=010|011₂

010₂=2₈

010011₂=23₈

011₂=3₈

1. Выполнить перевод числа 10110010₂ в восьмеричную систему счисления

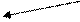10|110|010₂=010|110|010₂

010₂=2₈

110₂=6₈

010₂=2₈

10110010₂=262₈

1. Выполнить перевод числа 0,0010101₂ в восьмеричную систему счисления

0|010|101₂=000|010|101₂

000₂=0₈

010₂=2₈

101₂=5₈

0,0010101₂=0,025₈

Перевод из восьмеричную системы счисления в двоичную:

1. Выполнить перевод числа 13₈ в двоичную систему счисления

1₈=1₂=001₂;

3₈=11₂=011₂.

13₈ = 001|011₂.

После удаления незначащих нулей имеем 13₈=1011₂

1. Выполнить перевод числа 137₈ в двоичную систему счисления

1₈=001₂

3₈=011₂

7₈=111₂

001|011|111₂=1|011|111₂

13₈=1011111₂

1. Выполнить перевод числа 0,74₈ в двоичную систему счисления

7₈=111₂

0,74₈=0,111100₂

4₈=100₂.

Таблица 2. Основные методы

10→2		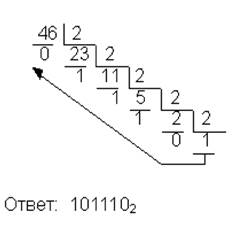2→10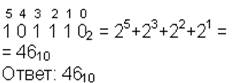
2→16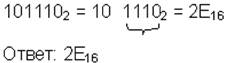
2→8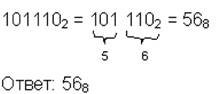
10→8		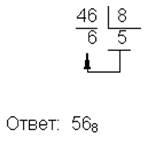8→2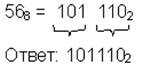
8→10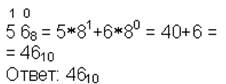
8→16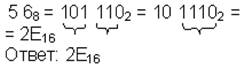
10→16		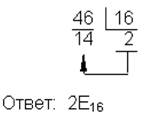16→2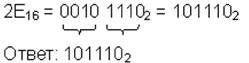
16→8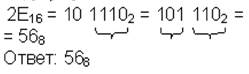
16→10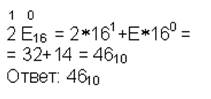

Арифметические операции в позиционных системах счисления

Сложение

Правила сложения в любой позиционной системе счисления аналогичны правилам сложения в десятичной системе счисления. При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

1. Сложим числа 15 и 6 в различных системах счисления.

Десятичная 15₁₀+6₁₀ Двоичная 1111₂+110₂ Восьмеричная 17₈+6₈

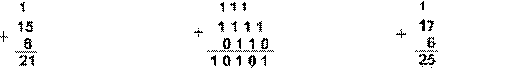
Шестнадцатеричная: F₁₆+6₁₆

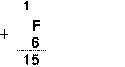
Проверка. Преобразуем полученные суммы к десятичному виду:
10101₂ = 2⁴ + 2² + 2⁰ = 16+4+1=21,
25₈ = 2∙8¹ + 5∙8⁰ = 16 + 5 = 21,
15₁₆ = 1∙16₁ + 5∙16₀ = 16+5 = 21.

Ответ: 15+6 = 21₁₀ = 10101₂ = 25₈ = 15₁₆

2. Сложим числа 15, 7 и 3.

Десятичная 15₁₀+7₁₀ +3₁₀ Двоичная 1111₂+111₂+11₂ Восьмеричная 17₈+7₈+3₈

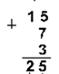
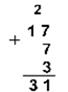
Шестнадцатеричная: F₁₆+7₁₆+3₁₆

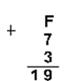
Проверка:
11001₂ = 2⁴ + 2³ + 2⁰ = 16+8+1=25,
31₈ = 3*8¹ + 1*8⁰ = 24 + 1 = 25,
19₁₆ = 1*16¹ + 9*16⁰ = 16+9 = 25.

Ответ: 15+7+3 = 25₁₀ = 11001₂ = 31₈ = 19₁₆.

Вычитание

1. Вычтем единицу из чисел 10₂, 10₈ и 10₁₆

Двоичная 10₂–1₂ Восьмеричная 10₈–1₈ Шестнадцатеричная 10₁₆–1₁₆

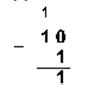
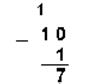
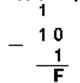
2. Вычтем единицу из чисел 100₂, 100₈ и 100₁₆.

Двоичная 100₂–1₂ Восьмеричная 100₈–1₈ Шестнадцатеричная 100₁₆–1₁₆

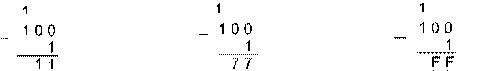
3. Вычтем число 59,75 из числа 201,25 в различных системах счисления

Десятичная 201,25₁₀ – 59,75₁₀ Двоичная 11001001,01₂–111011,11₂

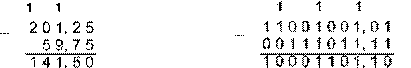
Восьмеричная 311,2₈–73,6₈ Шестнадцатеричная С9,4₁₆–3B,C₁₆

Ответ: 201,25₁₀ – 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆.