Доказательство окончено. Используя данную теорему можно установить полноту произвольной системы B

Используя данную теорему можно установить полноту произвольной системы B, выразив через функции этой системы все функции некоторой уже известной полной системы. Например, это может быть {x₁& x₂, x₁Ú x₂, }.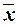

Рассмотрим несколько примеров.

1. B = {x₁& x₂, 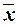}. Поскольку x₁& x₂ и 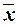содержатся в B, то для доказательства полноты этой системы достаточно выразить функцию 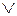через функции & и .

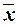Такое представление можно получить с помощью соотношения Де-Моргана 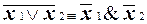. Поэтому 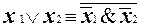, т.е. [B] = P₂.

2. B = {x₁Ú x₂, 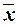}. Аналогично предыдущему случаю можно показать, что 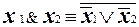. Такое представление, получается из второго соотношения Де-Моргана, т.е. B также является полной системой.

3. Пусть B = 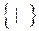. Напомним, что | называется функцией Шеффера и соответствует отрицанию конъюнкции x₁| x₂ º ( 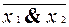). Тогда нетрудно проверить, что x | x º 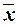, а (x₁| x₂) | (x₁| x₂) º x₁ & x₂.

Поэтому функция Шеффера образует полную систему.

Для доказательства неполноты произвольной системы B в некоторых случаях можно воспользоваться следующим методом, в котором:

1) выделяется специальное свойство, которым обладают все функции системы, но не обладают все булевы функции;

2) доказывается, что функции, представляемые формулами над B, также обладают выделенным свойством.

Тогда система B является неполной, поскольку существуют функции, имеющие свойство, которым не обладает ни одна функция из [B].

Пример. Рассмотрим систему B = {x₁+ 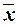₂, x }.

1. Нетрудно проверить, что обе функции из B на единичных наборах значений переменных равны 1 и этим свойством не обладает функция Шеффера.

2. Всякая формула над B представляет б.ф., которая на единичном наборе значений переменных принимает значение 1.

Следовательно, множество B не является полной системой.

ПОЛИНОМЫ ЖЕГАЛКИНА

Рассмотрим систему функций B = {x₁ x₂, x + 1}, где x₁ x₂ - это двоичное умножение.

Данная система является полной, поскольку x₁ x₂ совпадает с конъюнкцией x₁ & x₂, а x + 1 - это .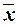

Пусть U - произвольная формула над B. Преобразуем ее по следующим правилам:

1) раскроем скобки в U; используя дистрибутивность сложения и умножения, получим сумму различных произведений переменных и констант 1;

2) в каждом произведении удалим все кратные вхождения одной и той же переменной (на основании тождества xx º x);

3) в каждом произведении переменных переставим переменные в порядке возрастания индексов (здесь применяется следующее тождество x_I & x_j º x_j & x_i);

4) удалим из полученной суммы все пары одинаковых слагаемых, используя тождество x + x º 0;

5) если в результате выполнения преобразований 1) – 4) получается пустая запись, то запишем результат в виде: 0.

Полученная в результате формула W, рассматриваемая с точностью до порядка записи слагаемых, носит название полинома Жегалкина.

Поскольку все преобразования, применявшиеся к исходной формуле U в процессе получения полинома W, являются эквивалентными преобразованиями, то полином W эквивалентен U.

Следовательно, всякая б.ф. представляется некоторым полиномом Жегалкина.

Пример. Рассмотрим функцию f = 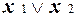. Она имеет следующее табличное задание:

x1 x2	x1Ú x2
0 0
0 1
1 0
1 1

Общий вид полинома Жегалкина для функции двух переменных можно записать так: a x₁ x₂ + b x₁ +g x₂ + d, где a, b, g, d - неопределенные коэффициенты из E₂, значения которых для функции f необходимо уточнить.

В полином Жегалкина общего вида с неопределенными коэффициентами последовательно подставим все различные двоичные наборы значений переменных x₁ и x₂, и приравняем полученные выражения значениям функции на соответствующих наборах. При этом на каждом шаге удается уточнить значение одного из коэффициентов полинома.

Для нулевого набора значений переменных имеем:

f(0,0) =0, т.е. d = 0;

Для следующего набора(0, 1):

f(0, 1) =1, т.е. g = 1.

Аналогично, f(1, 0) = 1, т.е. b = 1.

Наконец, f(1, 1) = 1 и a = 1.

Следовательно, f(x₁, x₂) = x₁ x₂ + x₁ + x₂.

Упражнение

1. Определить количество слагаемых в полиноме Жегалкина общего вида для n переменных x₁, . . . , x_n.

2. Привести пример записи общего вида полинома Жегалкина от n переменных x₁, . . . , x_n.

ТЕОРЕМА 4.6

Всякая булевская функция представляется единственным полиномом Жегалкина.

Доказательство

Покажем, что существует ровно 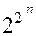различных полиномов Жегалкина, которые можно составить, используя символы переменных x₁, . . . , x_n.

1. С помощью символов переменных x₁, . . . , x_n можно составить 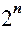разных произведений, в которых переменные располагаются слева направо в порядке возрастания индексов. К таким произведениям относится и пустое произведение, которое не содержит переменных и соответствует свободному члену полиномов Жегалкина.

Полиномы Жегалкина рассматриваются с точностью до порядка входящих в него слагаемых. Поэтому различных полиномов ровно столько, сколько существует различных подмножеств множества из 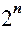различных произведений.

При этом пустое подмножество множества всех таких произведений соответствует полиному, равному0.

Поэтому существует ровно 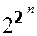различных полиномов, которые можно составить для переменных x₁, . . . , x_n.

Следовательно, число полиномов и число булевых функций для этих переменных совпадают. А так как каждая функция представляется некоторым полиномом, то такое представление единственно.

Справедливость данного заключения может быть проверена рассуждениями от противного с использованием комбинаторного правила птичьих гнезд.