Геометрическая интерпретация днф

Рассмотрим специальную интерпретацию соотношений эквивалентности 1 - 3, которая позволяет лучше понять, почему проводимые с помощью этих правил преобразования ДНФ приводят к получению минимальной ДНФ.

В дальнейшем будем рассматривать булевские функции для фиксированного множества обозначений переменных
{x₁, . . ., x _n}.

Двоичные числовые наборы длины n поставим в соответствие точкам n-мерного евклидова пространства. Тогда все n-элементные двоичные наборы образуют множество вершин единичного n-мерного куба. Для n = 3 такой куб имеет вид, приведенный на рис. 4.4.

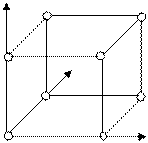x₃011 111

001 101

x₂

010110

x₁

000 100

Рис 4.4

Для произвольной б.ф. f обозначим как N_f - множество вершин единичного n-мерного куба, в которых f принимает значение 1.

Справедливы следующие свойства таких множеств для произвольных функций f₁ и f₂:

1) ;

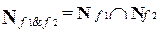2) .

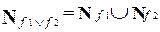Элементарная конъюнкция K = 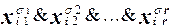, имеющая рангr, принимает значение 1на 2 ^n-r наборах значений переменных x₁, . . . , x_n.

Поэтому множество N_K, состоящее из вершин единичного n-мерного куба, в которых конъюнкция K равна 1, представляет собой(n – r)-мерную грань куба. Вершины такой грани соответствуют всем двоичным наборам, в которых переменные 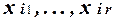принимают фиксированные значения 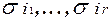, а остальные n - r переменных - произвольные значения. Заметим, что такая грань содержит 2 ^n-r вершин.

Например, для n = 4 и конъюнкции K = 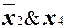множество N_K равно{(0001), (0011), (1001), (1011)}.

Для произвольной ДНФ D = справедливо равенство

N _D = .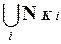

Это означает, что грани, на которых конъюнкции, входящие в ДНФ, равны 1, образуют покрытие множества N_D.

Справедливо и обратное утверждение: всякая (n – r)- мерная грань единичного n-мерного куба представляет собой множество точек, на которых обращается в 1 некоторая конъюнкция рангаr .

Действительно, если некоторая грань единичного n-мерного куба состоит из вершин, в которых значения переменных 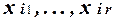фиксированы и соответственно равны 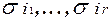, а остальные переменные принимают произвольные значения, то соответствующая такой грани конъюнкция имеет вид: .

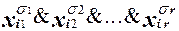Например, для n = 5 грань N, состоящая из вершин, в которых переменные x₁, x₂ и x₄ принимают фиксированные значения 1, 0 и 0, а значения остальных переменных произвольные, соответствует конъюнкции: K = .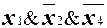

Следовательно, всякая ДНФ представляющая б.ф. f, порождает покрытие множества N _f , и наоборот, всякое покрытие множества N_f гранями единичного n-мерного куба порождает ДНФ, представляющую некоторую б.ф. f.

Заметим, что длина конъюнкции и размерность грани находятся в обратной зависимости. То есть, чем короче запись конъюнкции (или чем меньше ее ранг), тем больше размерность соответствующей грани.

Поэтому, чем больше размерности граней, покрывающих множество N_f, тем меньше сложность ДНФ, соответствующей такому покрытию.

Если заданы две конъюнкции K₁ и K₂ так, что запись K₁ является частью записи K₂, то для гране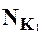й и 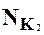справедливо включение 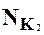Í 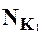Справедливо и обратное соотношение: если 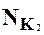Í 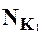то запись конъюнкцииK₁ является частью конъюнкции записи K₂.

Нетрудно видеть, что элементарные конъюнкции, входящие в состав минимальной ДНФ для функции f, должны соответствовать таким граням единичного n-мерного куба, которые содержатся в N_f , но не могут быть расширены.

ОПРЕДЕЛЕНИЕ

Конъюнкция K называется максимальной для функции f, если:

1)N_K ÍN _f;

2) 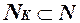, где N - произвольная грань единичного n-мерного куба, то N 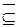N_f .

Грани единичного куба, соответствующие максимальным конъюнкциям функции f , называются максимальными гранями для f.

ТЕОРЕМА 4.3

Если D = K₁ 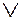. . . 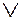K_r - это минимальная ДНФ для f, то всякая конъюнкция K_i является максимальной для f.

Доказательство

Предположим противное. Пусть D = K₁ 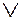. . . 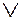K_r является минимальной ДНФ для некоторой б.ф. f, содержащей конъюнкцию K_i, которая не является максимальной для этой функции. Пусть K - это произвольная максимальная конъюнкция для f, такая что 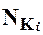Ì .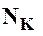

Рассмотрим ДНФ D^* = K₁ Ú. . . K_i-1 Ú K Ú K_i+1. . . ÚK_r .

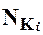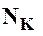Поскольку Ì Í 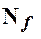, то D^* º D.

Но конъюнкция K короче конъюнкции K_i. Значит, справедливо неравенство L(D^*) < L(D), что противоречит предположению о минимальности ДНФ D.

Следовательно, все конъюнкции минимальной ДНФ D являются максимальными.

Доказательство окончено.

Например, для функции f = x₁ ® (x₂ ® x₃) множество N_f состоит из наборов, соответствующих выделенным вершинам куба, изображенного на рис. 4.5.

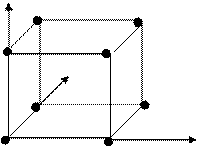x₃

011 111

001 101

x₂

010 110

000 100 x₁

Рис. 4.5

Соответствующие максимальные грани и определяемые ими конъюнкции имеют вид:

N₁ = {000, 001, 010, 011} K₁ = ;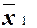

N₂ = {000, 001, 100, 101} K₂ = ;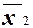

N₃ = {001, 011, 101, 111} K₃ = x_3.

Поскольку ни одна максимальная грань для f целиком не покрывается другими такими гранями, то минимальная ДНФ для f имеет вид .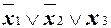

Рассмотрим введенные ранее соотношения эквивалентности в правилах поглощения, склеивания и обобщенного склеивания.

Правила поглощения и склеивания позволяют выполнять упрощение ДНФ либо за счет удаления из покрытия множества N_f таких граней, которые целиком содержатся в других гранях, либо за счет объединения пары противоположных граней в одну грань.

Правило обобщенного склеивания позволяет включать в покрытие множества N_f такие конъюнкции, с помощью которых можно в последующем организовать последовательность применения правил поглощения и склеивания, ведущую к получению более простой ДНФ.

Например, без правила обобщенного склеивания невозможно осуществить преобразование 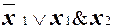ДНФ в ДНФ .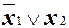

ОПРЕДЕЛЕНИЕ

ДНФ D называется сокращенной ДНФ функции f, если она состоит из всех максимальных конъюнкций для f.

Из теоремы 4.3 следует, что минимальная ДНФ получается из сокращенной ДНФ удалением некоторых (возможно, ни одной) конъюнкций.

Для построения сокращенной ДНФ произвольной б.ф., отличной от тождественного нуля, можно воспользоваться методом Блейка который будет приведен без доказательства.

Возьмем СДНФ для f и последовательно применим к этой дизъюнктивной форме следующие преобразования:

1) пока это возможно, применяется правило обобщенного склеивания к конъюнкциям исходной СДНФ и получаемых из нее ДНФ;

2) к полученной в результате первого преобразования ДНФ применимы правила поглощения и склеивания, пока это возможно.

Упражнение. Сформулировать геометрическую интерпретацию правил поглощения, склеивания и обобщенного склеивания в терминах граней единичного n-мерного куба.