В – это одиннадцать в десятичной системе, плюс 9 и один получается 21, что соответствует 15 в шестнадцатеричной системе. Пять пишем, один в уме

F – это пятнадцать в десятичной системе, плюс 5 и один получается 21, что соответствует 15 в шестнадцатеричной системе. Пять пишем, один в уме и т.д.

Следовательно,

10001101,101₂ + 1110110,11₂ = 100000100,011₂;

673,315₈ + 47214,15₈ = 50107,465₈;

1E7F,9A₁₆ + 355,B7₁₆ = 21D5,51₁₆.

Пример 4. Выполнить вычитание чисел в различных системах счисления:

§ 100000100,011₂ - 10001101,101₂;

§ 50107,467₈ - 673,315₈;

§ 21D5,51₁₆ - 1E7F,9A₁₆.

Решение. Вычитание чисел происходит по тем же правилам, что и в десятичной СС.

Рассуждать, например, для шестнадцатеричной системы, можно следующим образом:

А – это десять в десятичной системе, от одного нельзя отнять десять, занимаем шестнадцать. Шестнадцать плюс 1 получается 17, минус десять – получается 7.

От пяти один заняли, осталось 4, от четырех нельзя отнять девять, занимаем шестнадцать. Шестнадцать плюс 4 получается 20, минус девять – получается 11. Одиннадцать – это В в шестнадцатеричной системе и т.д.

Пример 7.Выполнить умножение чисел в различных системах счисления:

§ 111₂*11₂;

§ 52₈*16₈;

§ 17,А₁₆*35₁₆

Решение. При выполнении умножения можно использовать обычный алгоритм перемножения чисел в столбик.

_

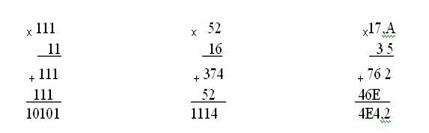
Рассуждать, например, для шестнадцатеричной системы, можно следующим образом:

А – это десять в десятичной системе, умножить на 5 получается 50, что соответствует 32 в шестнадцатеричной системе. Два пишем, три в уме.

Умножить на 5 равно 35 и три в уме получается 38, что соответствует 26 в шестнадцатеричной системе. Шесть пишем, два в уме.

Умножить на 5 и 2 в уме получается 7.

Аналогично производится умножение на 3, получается 46Е.

Сложив 762 и 46Е, получается 4Е42.

Пример 8.Выполнить деление чисел в различных системах счисления:

§ 110101111010₂ :10010110₂;

§ 4634₈ :244₈;

§ 43₈ :16₈.

Решение. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной СС.

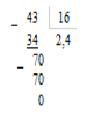
Содержание работы

2.1 Перевести числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверить результаты, выполнив обратные переводы:

а) 125₁₀; б)229₁₀; в) 88₁₀; г) 37,25₁₀ ; д) 206,125₁₀.

2.2 Перевести числа из двоичной системы в восьмеричную и шестнадцате­ричную, а затем проверить результаты, выполнив обратные переводы:

а) 100111111011101,11₂; в) 101111111101,111₂; д) 1011110011,10011₂;б) 10111001101100,111₂; г) 11101010111011,101₂; е) 1100010101,11001₂ .

2.3 Перевести в двоичную и восьмеричную системы шестнадцатеричные числа:

а) 2СЕ_]6; б) 9F40₁₆; в) ABCDE₁₆; г) 1010,101₁₆; д) 1ABC,9D₁₆.

2.4 Выписать целые числа:

а) от 101101₂ до 110000₂ в двоичной системе;

б) от 202₃ до 1000₃ в троичной системе;

в) от 14₈до 20₈ в восьмеричной системе;

г) от 28₁₆ до 30₁₆ в шестнадцатеричной системе.

2.5 Сложить числа, а затем проверить результаты, выполнив соответствующие десятичные сложения:

а) 101ll0l₂ и 1110111₂; д) 37₈ и 75₈; и) А₁₆ и F₁₆

б) 1011,101₂ и 101,011₂; е) 165₈ и 37₈; к) 19₁₆ и С₁₆

в) 1011_2,11₂ и 111,1₂; ж) 7,5₈ и 14,6₈; л) А,В₁₆ и Е,F₁₆

г) 1011₂,11,1₂ и 111₂; з) 6₈,17₈ и7₈; м)Е₁₆ , F₁₆ и 9₁₆

2.6 В какой системе счисления выполнены следующие сложения? Найти основания каждой системы:

а) 98 б) 1345 в) 10101 г) 765 д) 98

⁺ 89⁺ 2178 + 1111 +576 +56

121 3523 1011 677 79

20000 2462 167

2.7 Вычесть:

а) 111₂ из 10100₂; д) 15₈ из 20₈ ; и) 1А₁₆ из 31₁₆

б) 10,11₂ из 100,1₂; е) 47₈ из 102₈ ; к) F9E₁₆ из 2А30₁₆

в) 111,1₂ из 10010₂; ж) 56,7₈ из 101₈ ; л) D,l₁₆ из B,92₁₆

г) 10001₂ из 1110,11₂; з) 16,54₈ из 30,01₈ ; м) ABC₁₆ из 5678₁₆.

2.8 Перемножить числа, а затем проверить результаты, выполнив соответствующие десятичные умножения:

а) 101101₂ и 101₂; д) 37₈ и 4₈;

б) 111101₂ и 11,01₂; е) 16₈ и 7₈;

в) 1011,11₂ и 101,1₂; ж) 7,5₈ и 1,6₈;

г) 10001₂ и 1111,001₂; з) 6,25₈ и 7,12₈.

2.9 Разделить 10010110₂ на 1010₂ и проверить результат, умножая делитель на частное.

2.10 Разделить 10011010100₂ на 1100₂ и затем выполнить соответствующее деся­тичное и восьмеричное деление.

2.11 Вычислить значение выражения:

а) 256₈+10110,1₂ -(60₈+12₁₀)-lF_]6;

б) 1AD_]6-100101100₂: 1010₂ + 217₈;
в) 1010₁₀ + (106₁₆- 11011101₂) - 12₈;
г) 1011₂ • 1100₂: 14₈ + (100000₂-40₈).

2.12 Расположить следующие числа в порядке возрастания:

а) 74₈, 110010₂, 70₁₀, 38₁₆; в) 777₈, 101111111₂, 2FF₁₆, 500₁₀;

б) 6Е₁₆, 142₈, 1101001₂, 100₁₀; г) 100₁₀, 1100000₂, 60₁₆, 141₈.

2.13 В какой системе счисления справедливо равенство:

а) 20 + 25 = 100; б) 22 + 44 = 110?