Синтаксическая мера информации
Меры и единицы представления, измерения и хранения информации
Информациейназывают сведения о тех или иных объектах, явлениях или процессах в окружающей среде. Любая форма человеческой деятельности и связана с передачей обработкой информации. Она необходима для правильного управления окружающей действительностью, достижения поставленных целей и, в конечном счете - для существования человека. Любая система: социально-экономическая, техническая, или система в живой природе действует в постоянной взаимосвязи с внешней средой – другими системами более высокого и более низкого уровней. Взаимосвязь осуществляется посредством информации, которая передает как команды управления, так и сведения, необходимые для принятия правильных решений. Понятие информации как важнейшего элемента системы, охватывающего все стороны ее жизнедеятельности можно считать универсальным, применимым к любым системам.
Единого научного мнения о количественном смысле понятия "информация" не существует. Разные научные направления дают различные определения исходя из тех объектов и явлений, которые они изучают. Некоторые из них считают, что информация может быть выражена количественно, давая определения количества и объема информации (меры информации), другие ограничиваются качественными толкованиями.
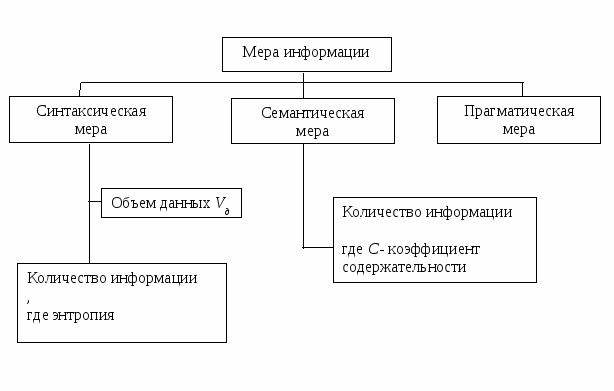
Синтаксическая мера информации
Синтаксическая мера информации используется для количественного выражения обезличенной информации, не выражающей смыслового отношения к объектам.
Объем данных Vд в сообщении измеряется количеством символов в нем. Обычно для указания объема данных считают количество двоичных символов. Двоичный символ может принимать только два различных значения: 1 и 0 (эквивалентно значениям "да" и "нет"). Двоичный символ носит название бит(от слов binarydigit- двоичная цифра). Распространенность двоичной единицы измерения объема объясняется двоичной системой записи чисел, на которой основаны современные компьютеры. Традиционно применяется также байт (byte), равный 8 битам.
Предположим, получатель информации (наблюдатель) дважды принял одно и то же сообщение. Он получил двойной объем данных, но получил ли он двойное количество информации? Интуиция подсказывает, что нет - вторая копия не содержала новых сведений. Информацию, содержащуюся в сообщении, можно трактовать в аспекте того, насколько она была ранее неизвестна и, следовательно, является новой или неожиданной.
Количество информации I определяется через понятие неопределенности состояния (энтропию). Приобретение информации сопровождается уменьшением неопределенности, поэтому количество информации можно измерять количеством исчезнувшей неопределенности.
Пусть в сообщении наблюдателем получены сведения о некоторой части реальности (системе). До принятия сообщения получатель имел некоторые предварительные (априорные) сведения a о системе. Мерой его неосведомленности о системе является функция H(a), которая в то же время служит и мерой неопределенности состояния системы.
После получения сообщения b получатель приобрел в нем информацию Ib(a), уменьшившую его неосведомленность (неопределенность состояния системы) так, что она стала равна Hb(a). Тогда количество информации Ib(a) о системе, полученной в сообщении b, определится как Ib(a) =H(a) -Hb(a) .
Таким образом, количество информации в сообщении измеряется изменением (уменьшением) неопределенности состояния системы после получения сообщения.
Если конечная неопределенность Hb(a) обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации Ib(a) =H(a). Иными словами, энтропия системы H(a) может рассматриваться как мера информации.
Энтропия системы H(a), имеющей Nвозможных состояний, согласно формуле Шеннона равна
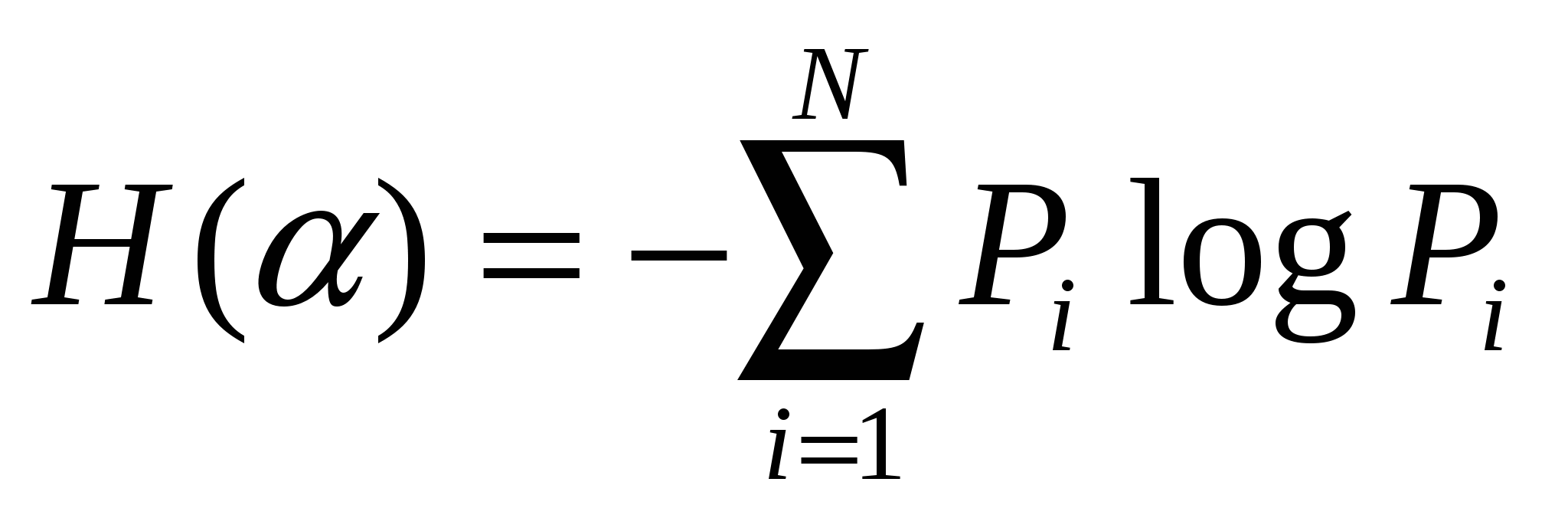 ,
,
гдеPi - вероятность того, что система находится в i-м состоянии.
Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны 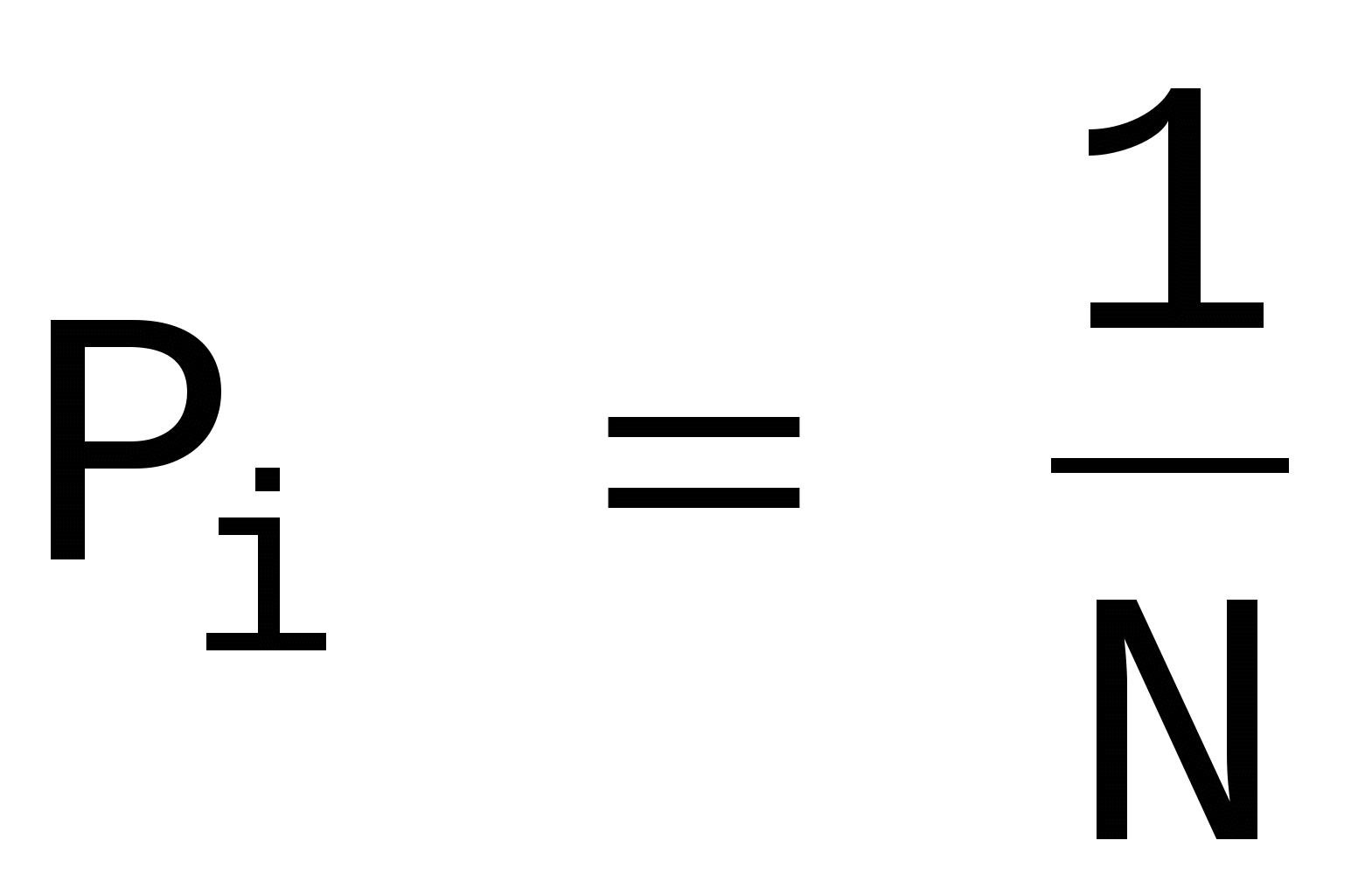 ,
,
энтропия определяется соотношением
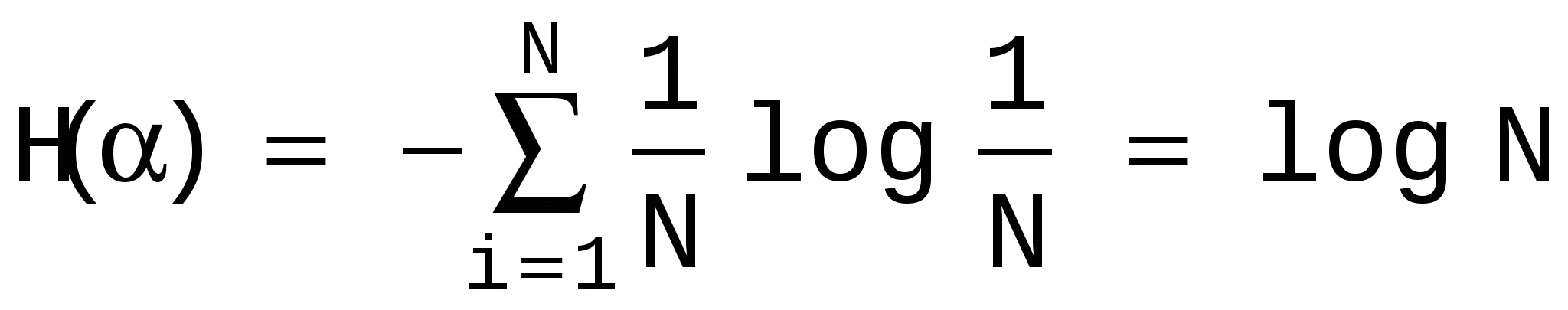 .
.
Часто информация кодируется числовыми кодами в той или иной системе счисления. Одно и то же количество цифр (символов) в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения
N=mn,
где N- число всевозможных отображаемых состояний;
m- основание системы счисления (разнообразие символов, применяемых в алфавите);
n- число символов в сообщении.
Приведем пример. По каналу связи передается n- символьное сообщение, использующее m различных символов. Так как количество всевозможных кодовых комбинаций будет N=mn, то при равной вероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет равно
I = log N = n log m.
Эта формула известна как формула Хартли. Если в качестве основания логарифма принять m, то I=n. В данном случае количество информации (при условии полного априорного незнания абонентом содержания сообщения) будет равно объему данных I=Vд , полученных по каналу связи. Для не равновероятных состояний системы всегда I<Vд=n.
Наиболее часто логарифм берут по основанию 2. В этом случае количество информации измеряют в битах.
Коэффициент информативности сообщения определяется отношением количества информации к объему данных, т.е.
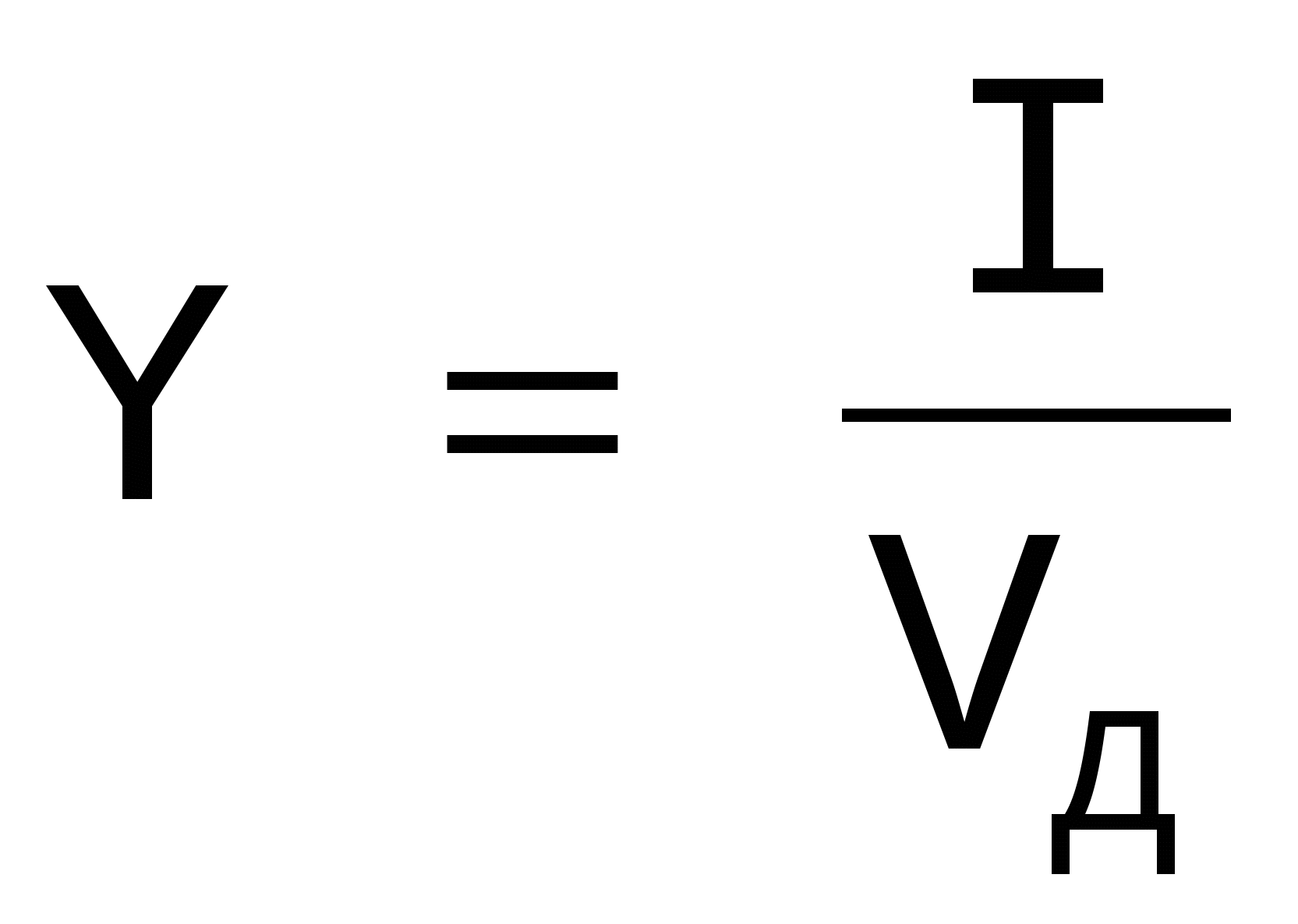 , причем 0 <Y< 1 .
, причем 0 <Y< 1 .
C увеличением Y уменьшаются затраты на обработку информации. Поэтому обычно стремятся к повышению информативности.
Семантическая (смысловая) адекватность.Эта форма определяет степень соответствия образа объекта и самого объекта. Семантический аспект предполагает учет смыслового содержания информации. На этом уровне анализируются те сведения, которые отражает информация, рассматриваются смысловые связи. В информатике устанавливаются смысловые связи между кодами представления информации. Эта форма служит для формирования понятий и представлений, выявления смысла, содержания информации и ее обобщения.
Прагматическая (потребительская) адекватностьотражает отношение информации и потребителя, соответствие информации цели управления, которая на ее основе реализуется. Прагматические свойства информации проявляются только при наличии единства информации (объекта), пользователя и цели управления. Прагматический аспект рассмотрения связан с ценностью, полезностью использования информации при выработке потребителем решения для достижения своей цели.
События, виды событий
Опыт, эксперимент, наблюдение явления или некоторого процесса называется испытанием. Примеры испытаний: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесённой на каждую из шести граней цифры от одного до шести), реализация некоторого физического, механического или технологического процесса и т.д. При бросании монеты исходами (событиями) являются выпадение герба или выпадение цифры, а при бросании игральной кости — выпадение какой либо цифры на верхней грани кости. Испытания сопровождаются их исходами (событиями).
Событие — это качественный и (или) количественный результат испытания (исход), осуществляемого при определённой совокупности условий. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д.
Различают следующие типы событий: случайные события, совместные или несовместные события, достоверные или невозможные события, зависимые или независимые события, равновозможные события, элементарные (простые, неразложимые) события, событие или совокупность событий (исходов), благоприятствующих какому-либо другому событию.
Случайное событие – это результат испытания (или величина), которые нельзя заранее спрогнозировать, т.е. нельзя сказать, произойдёт это событие или не произойдёт, или, если событие произойдёт, то неизвестно, какое значение примет результат этого события.
Случайные события – первичные, неопределяемые (в строгом смысле) понятия в теории вероятностей, аналогичные понятиям точки и прямой – в геометрии.
Например, пусть игральная кость с пронумерованными гранями от 1 до 6 подбрасывается два раза. В этом опыте можно рассматривать следующие события: событие А – оба раза выпадет число 1; событие В – хотя бы один раз выпадет число 3; событие С – сумма выпавших чисел равна 8 и т.д.
Событие, которое обязательно наступит (никогда не произойдёт) в данном опыте, называется достоверным (невозможным). Достоверное событие обозначают символом Ω, а невозможное – Æ. Например, в опыте, состоящем в подбрасывании кости один раз – событие А – выпадение одного из чисел 1,2,3,4,5,6 – есть достоверное, а событие В – выпадение числа 7 – невозможное.
Два случайных события называются несовместными, если наступление одного из них исключает наступление другого в одном и том же испытании. (Таким образом, несовместные события не могут наступать одновременно). В противном случае, т.е. если наступление одного события не исключает наступление другого события в одном и том же испытании, то эти события называются совместными. Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.
События А1, А2, … , Аn называются попарно несовместными, если любые два из них являются несовместными.
События называются равновозможными, если ни одно из них не является более возможным по сравнению с другими событиями.
События называются независимыми (зависимыми), если числовая характеристика возможности наступления одного события не зависит (зависит) от числовых характеристик наступления других событий (указанные числовые характеристики некоторых событий А, В, С, … называются вероятностями этих событий).
Определение. Совокупность попарно несовместных событий образуют полную группу событий для данного испытания, если в результате каждого испытания происходит одно и только одно из них.
Примеры полных групп событий: а) выпадение герба {Г} и выпадение цифры {Ц} при одном бросании монеты; б) попадание в цель и промах при одном выстреле по мишени; в) выпадение цифр «1», «2», «3», «4», «5», «6» при одном бросании кости.
Операции над событиями
Определение 1. Говорят, что в некотором опыте событие А влечёт за собой появление события В, если при наступлении события А наступает и событие В. Обозначение этого определения А Ì В. В терминах элементарных событий это означает, что каждое элементарное событие, входящее в А, входит также и в В.
Определение 2. События А и В называются равными или эквивалентными (обозначается А = В), если А Ì В и В Ì А, т.е. А и В состоят из одних и тех же элементарных событий.
Достоверное событие представляется объемлющим множеством Ω, а невозможное событие – пустым подмножеством Æ в нём. Несовместность событий А и В означает, что соответствующие подмножества А и В не пересекаются:А∩В = Æ.
Определение 3. Суммой двух событий А и В (обозначаетсяС = А + В) называется событие С, состоящее в наступлении по крайней мере одного из событий А или В (союз «или» для суммы является ключевым словом), т.е. наступает или А, или В, или А и В вместе.
Пример. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B — в том, что в мишень попадает 2-й стрелок. Событие A + B  означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков (1-й стрелок или 2-й стрелок, или оба стрелка).
означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков (1-й стрелок или 2-й стрелок, или оба стрелка).
Аналогично, суммой конечного числа событий А1, А2, …, Аn (обозначается А = А1 + А2 + … + Аn) называется событие А, состоящее в наступлении хотя бы одного из событий Аi (i = 1, … , n), или произвольной совокупности Аi (i = 1, 2, … , n).
Пример. Суммой событий А, В, С является событие, состоящее в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С, А или В, А или С, В или С, А или В или С.
Определение 4. Произведением двух событий А и В называется событие С (обозначается С = А ∙ В), состоящее в том, что в результате испытания произошли и событие А, и событие В одновременно. (Союз «и» для произведения событий является ключевым словом).
Аналогично произведением конечного числа событий А1, А2, …, Аn(обозначается А = А1 ∙А2 ∙…∙ Аn) называется событие А, состоящее в том, что в результате испытания произошли все указанные события.
Пример. Если события А, В, С есть появление «герба» в первом, во втором и третьем испытании соответственно, то событие А × В × С есть выпадение «герба» во всех трех испытаниях.
Замечание 1. Для несовместных событий А и В справедливо равенство А ∙ В = Æ, где Æ – невозможное событие.
Замечание 2. События А1, А2, … , Аn образуют полную группу попарно несовместных событий, если 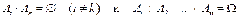 .
.
Определение 5. Противоположными событиями называются два единственно возможных несовместных события, образующие полную группу. Событие, противоположное событию А, обозначается 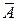 . Событие
. Событие 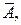 противоположное событию А, является дополнением к событию А до множества Ω.
противоположное событию А, является дополнением к событию А до множества Ω.
Для противоположных событий одновременно удовлетворяются два условия А ∙ 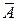 = Æ и А +
= Æ и А + 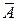 = Ω.
= Ω.
Определение 6. Разностью событий А и В (обозначается А – В) называется событие, состоящее в том, что событие А наступит, а событие В – нет и она равна А – В = А× 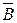 .
.
Отметим, что события А + В, А ∙ В, 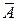 , А – В удобно трактовать в графическом виде с помощью диаграмм Эйлера – Венна
, А – В удобно трактовать в графическом виде с помощью диаграмм Эйлера – Венна
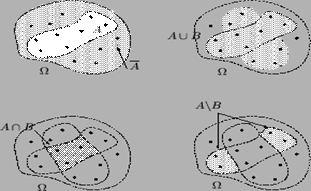
Операции над событиями: отрицание, сумма, произведение и разность
Сформулируем пример так: пусть опыт G заключается в проведении стрельбы наугад по области Ω, точки которого являются элементарными событиями ω. Пусть попадание в область Ω есть достоверное событие Ω, а попадание в области А и В – соответственно события А и В. Тогда события 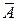 , А+В (или А È В – светлаяобласть на рисунке), А ∙ В (или А Ç В – область в центре), А – В (или А \ В – светлые подобласти)будут соответствовать четырем изображениям на рисунке. В условиях предыдущего примера со стрельбой двух стрелков по мишени произведением событий А и В будет событие С = А Ç В, состоящее в попадании в мишень обоими стрелками.
, А+В (или А È В – светлаяобласть на рисунке), А ∙ В (или А Ç В – область в центре), А – В (или А \ В – светлые подобласти)будут соответствовать четырем изображениям на рисунке. В условиях предыдущего примера со стрельбой двух стрелков по мишени произведением событий А и В будет событие С = А Ç В, состоящее в попадании в мишень обоими стрелками.
Замечание 3. Если операции над событиями представить как операции над множествами, а события представить как подмножества некоторого множества Ω, то сумме событий А+В соответствует объединение АÈВ этих подмножеств, а произведению событий А ∙ В — пересечение А∩В этих подмножеств.
Таким образом, операции над событиями можно поставить в соответствие операцию над множествами.
| Обозначения | Язык теории вероятностей | Язык теории множеств |
| Ω | Пространство элемент. событий | Универсальное множество |
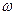 | Элементарное событие | Элемент из универсального множества |
| А | Случайное событие | Подмножество элементов ω из Ω |
| Ω | Достоверное событие | Множество всех ω |
| Æ | Невозможное событие | Пустое множество |
| АÌ В | А влечёт В | А – подмножество В |
| А+В (А ÈВ) | Сумма событий А и В | Объединение множеств А и В |
| А× В (А Ç В) | Произведение событий А и В | Пересечение множеств А и В |
| А – В (А \ В) | Разность событий | Разность множеств |
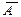 | 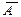 – событие, противоположное событию А, т.е. не А – событие, противоположное событию А, т.е. не А | Дополнение множества А до множества Ω 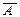 = Ω \ А = Ω \ А |
Действия над событиями обладают следующими свойствами:
• А + В = В + А, А ∙ В = В ∙ А (переместительное);
• (А + В) ∙ С = А × С + В × С, А ∙ В + С = (А + С) × (В + С) (распределительное);
• ( А + В ) + С = А + (В + С), (А ∙ В) ∙ С = А ∙ (В ∙ С) (сочетательное);
• А + А = А, А ∙ А = А;
• А + Ω = Ω, А ∙ Ω = А;
• А + 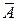 = Ω, А ∙
= Ω, А ∙ 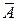 = Æ;
= Æ;
• 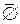 = Ω,
= Ω, 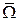 = Æ,
= Æ, 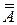 = А;
= А;
• А – В = А ∙ 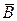 ;
;
• 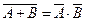 и
и 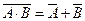 — законы де Моргана.
— законы де Моргана.
В справедливости этих свойств можно убедиться с помощью диаграмм Эйлера-Венна, а также на основе численного подхода, если сопоставить появлению некоторого события цифру «1», а не появлению этого события – цифру «0». Тогда следующие операции над событиями: А + В, А ∙ В, 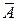 – иллюстрируются в следующей таблице.
– иллюстрируются в следующей таблице.
| А | В | А+В | А ∙ В | А | 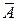 |
Законы де Моргана доказываются путем составления табл.
