Описание практической части работы
2.1. Цели лабораторной работы: Ознакомиться с понятием алгоритм, его свойствами и способами представления. Изучить основные положения ГОСТ 19.701-90 (ИСО 5807-85), связанные с изображением схем программ (графическим представлением алгоритма). Изучить построение линейных и разветвляющихся алгоритмов.
2.2. Постановка задачи: В соответствии с номером варианта (табл.1, 2) найти значение функции, заданной одним или несколькими математическими выражениями и для дискретной функции, заданной на нескольких интервалах. Разработать и описать два алготитма: с линейной и разветвляющейся структурой.
2.3. Порядок выполнения работы:
2.3.1. Ознакомиться с теоретической частью.
2.3.2. Получить задание у преподавателя.
2.3.3. Выполнить работу.
2.3.4. Оформить отчет:
2.4.1. Содержание отчета:
1. Цель работы - краткая формулировка поставленной цели.
2. Порядок выполнения - определяются действия, необходимые для выполнения данной работы.
3. Постановка задачи - формулирование задачи в соответствии с индивидуальным заданием.
4. Решение поставленной задачи:
4.1. Математическое описание решения поставленной задачи содержит описание связей между параметрами с использованием принятых в математике обозначений.
Описание логической структуры программы (алгоритм решения) содержит:
- краткое описание схемы программы,
- алгоритм решения (по ГОСТ ) - рисунок,
Выводы - отвечают на поставленную цель.
2.4. Контрольные вопросы
1 Дайте определение алгоритма ?
2 Назовите свойства алгоритмов?
3 Каким образом можно описать алгоритм решения задачи ?
4 Чем характеризуется линейная структура алгоритма ?
5 Как определяется разветвляющаяся структура алгоритма ?
6 Чем характеризуется полная и неполная альтернатива ?
7 В каких случаях используется конструкция выбора ?
8. Может ли разветвляющаяся структура иметь ветвь, направленную к началу программы ?
9. Если в алгоритме два условия (блока решения) стоят в одной ветви, где заканчивается первое и второе условия ?
10. Сколько условий можно записать в одном блоке решения ?
Таблица 1.
Задания для составления линейного алгоритма
| n | Функция y(x) | n | Функция y(x) |
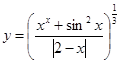 | 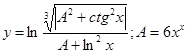 | ||
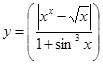 | 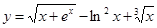 | ||
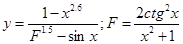 | 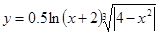 | ||
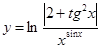 | 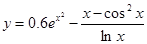 | ||
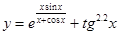 | 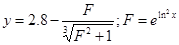 | ||
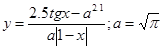 | 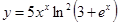 | ||
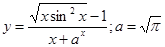 | 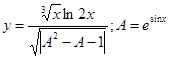 | ||
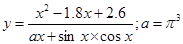 | 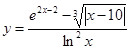 | ||
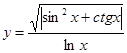 | 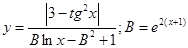 | ||
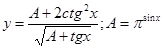 | 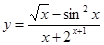 | ||
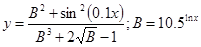 | 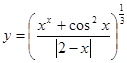 | ||
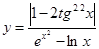 | 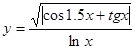 | ||
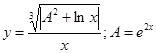 | 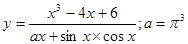 | ||
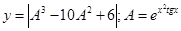 | 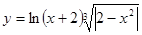 | ||
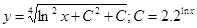 | 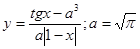 |
Таблица 2.
Задания для составления разветвляющегося алгоритма
| n | задание | n | задание |
 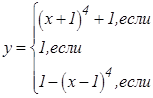 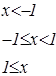 | 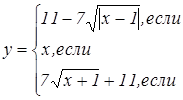 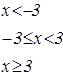 | ||
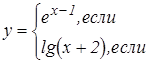 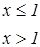 | 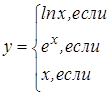 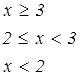 | ||
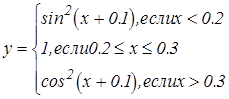 | 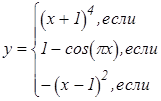 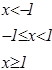 | ||
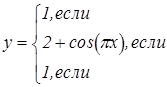 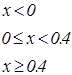 | 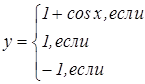 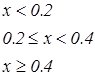 | ||
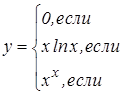 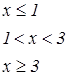 | 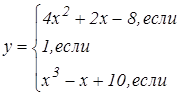 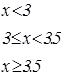 | ||
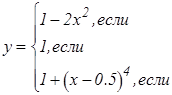 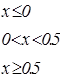 | 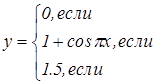 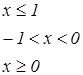 | ||
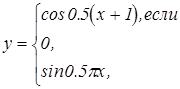 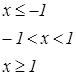 | 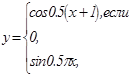 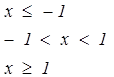 | ||
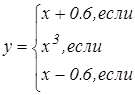 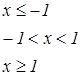 | 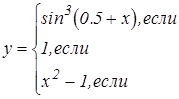 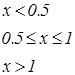 | ||
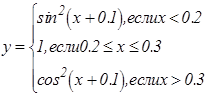 | 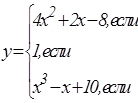 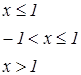 | ||
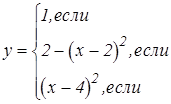 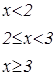 | 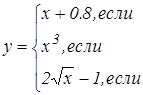 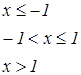 | ||
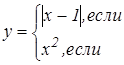 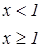 | 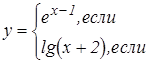 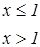 | ||
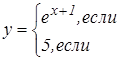 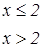 | 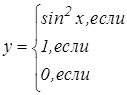 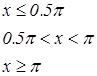 | ||
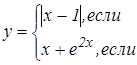 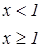 | 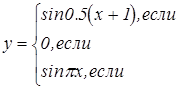 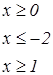 | ||
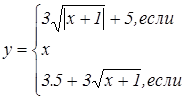 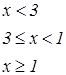 | 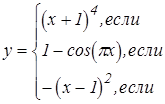 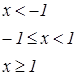 | ||
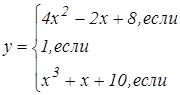  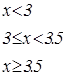 | 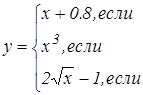 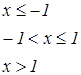 |
