Практическая иллюстрация декомпозиции, сравнительных суждений и синтеза

Для иллюстрации изложенных выше идей вернемся к ЛПР, который должен из трех альтернативных решений выбрать наилучший вариант производственной программы.

В табл. 4.6 представлена еще раз матрица парных сравнений для второго уровня иерархии, которая содержит шесть критериев, воздействующих на общую цель.

Таблица 4.6

Выбор наилучшего варианта плана: матрица попарных сравнений для уровня 2

Пара- метры							Произведение элементов строк	Вектор приоритетов
								2,492883
	1/2					1/2		1,955981
	1/3	1/4					8,6625	1,4330091
	1/5	1/7	1/7			1/8	0,00196	0,353761
	1/4	1/8	1/5	1/4		1/6	0,00027	0,254231
	1/2		1/3				15,84	1,584744
Сумма	2,78	5,515	8,67	28,25		6,795		8,074691

Вычислим на данном этапе расчетов вектор приоритетов, собственное значение 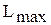, индекс согласованности и отношение согласованности. В результате вычисления сумм по строкам получим:

По первой строке: 1 × 2 × 3 × 5 × 4 × 2 = 240.

По второй строке: 0,5 × 1 × 4 × 7 × 8 × 0,5 = 56.

По третьей строке: 0,33 × 0,25 × 1 × 7 × 5 × 3 = 8,6625.

По четвертой строке: 0,2 × 0,14 × 0,14 × 1 × 4 × 0,125 = 0,00196.

По пятой строке: 0,25 × 0,125 × 0,2 × 0,25 × 1 × 0,17 = 0,00027.

По шестой строке: 0,5 × 2 × 0,33 × 8 × 6 × 1 = 15,84.

Рассчитанные числовые данные отражены в соответствующем столбце табл. 4.6.

Вычисление вектора приоритетов:

По первой строке: 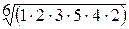= 2,492883.

По второй строке: 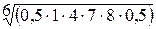= 1,955981.

По третьей строке: 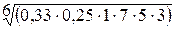= 1,433091

По четвертой строке: 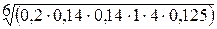= 0,353761.

По пятой строке: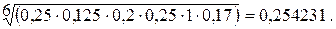

По шестой строке: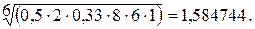

Полученные числовые данные отражены в табл. 4.6 в соответствующем столбце.

Расчет числовых оценок нормализованного вектора приоритетов по строкам осуществляется следующим образом.

По строке 1: 2,492883 : 8,074691 = 0,309.

По строке 2: 1,955981 : 8,074691 = 0,242.

По строке 3: 1,433091 : 8,074691 = 0,177.

По строке 4: 0,353761 : 8,074691 = 0,044.

По строке 5: 0,254231 : 8,074691 = 0,031.

По строке 6: 1,584744 : 8,074691 = 0,196.

В качестве примера приведем процедуру суммирования данных по столбцам на примере первого из них:

1 + 0,5 + 0,33 + 0,2 + 0,25 + 0,5 = 2,78.

Полученная расчетным путем информация отражена в табл. 4.7.

Таблица 4.7

Выбор наилучшего варианта плана: матрица попарных сравнений для уровня 2

Критерии							Вектор приорите- тов	Оценка нормализованного вектора
							2,492883	0,309
	1/2					1/2	1,955981	0,242
	1/3	1/4					1,433009	0,177
	1/5	1/7	1/7			1/8	0,353761	0,044
	1/4	1/8	1/5	1/4		1/6	0,254231	0,031
	1/2		1/3				1,584744	0,196
Сумма	2,78	5,515	8,67	28,25		6,795	-	-

Определяем наибольшее значение матрицы суждений. Для этого сумму первого столбца умножаем на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца умножается на вторую компоненту нормализованного вектора приоритетов и т.д.

В результате расчетов получим:

По первой строке: 2,78 × 0,309 = 0,859.

По второй строке: 5,515 × 0,242 = 1,335.

По третьей строке: 8,67 × 0,177 = 1,535.

По четвертой строке: 28,25 × 0,044 = 1,243.

По пятой строке: 28 × 0,031 = 0,868.

По шестой строке: 6,795 × 0,196 = 1,332.

В этом случае наибольшее собственное значение матрицы суждений будет равно:

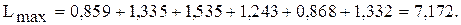
Определим численное значение индекса согласованности (ИС):

ИС = ,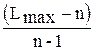

где n - число сравниваемых элементов.

В нашем случае получим ИС = (7,172 - 6) : 5 = 0,234.

Определим отношение согласованности (ОС) элементов матрицы. Для этого воспользуемся средними согласованиями для случайных матриц разного порядка.

Размер матрицы
Случайная согласованность ( 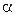)			0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49

В нашем случае отношение согласованности составит:

ОС = ИС : 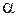= 0,234 : 1,24 = 0,19 (т.е. 19%).

Величина ОС не должна быть более 20%. Если ОС выходит за эти пределы, то ЛПР, решающий задачу, должен заново исследовать содержательную ее сторону и соответствующие количественные оценки элементов и внести необходимые изменения в исходные данные.

В отношении матрицы попарных сравнений для уровня 3 вычислим векторы приоритетов, наибольшее собственное значение матрицы суждений, индекс согласованности (ИС) и отношение согласованности (ОС).

Результаты подобных расчетов в сводном виде приведены в табл. 4.8.

Из 6 приведенных выше критериев выбираем главные 3 и оцениваем их друг относительно друга, заполняем таблицу.

Таблица 4.8

Результаты расчетов по матрице попарных сравнений для уровня 3

Критерий 1	А	Б	В	Оценка нормализованного вектора	Критерий 2	А	Б	В	Оценка нормализованного вектора
А		1/3	1/5	0,104	А		1/4	1/5	0,082
Б			1/3	0,258	Б			1/7	0,184
В				0,638	В				0,733
Сумма:		4,33	1,53	Lmax = = 3,061	Сумма:		8,25	1,34	Lmax = = 3,12
				ИС=0,03					ИС=0,06
				ОС=0,05					ОС=103
Критерий 3	А	Б	В	Оценка нормализованного вектора	Критерий 4	А	Б	В	Оценка нормализованного вектора
А		1/7	1/5	0,091	А		1/3	1/5	0,14
Б				0,671	Б				0,585
В		1/4		0,238	В		1/4		0,275
Сумма:		1,39	5,5	Lmax = = 3,16	Сумма:		1,58	5,5	Lmax = = 3,217
				ИС=0,08					ИС=0,11
				ОС=0,14					ОС=0,19
Критерий 5	А	Б	В	Вектор приоритетов	Критерий 6	А	Б	В	Вектор приоритетов
А		1/4	1/3	1,114	А		1/3	1/4	0,108
Б			1/5	0,242	Б			1/5	0,211
В				0,644	В				0,679
Сумма		6,25	1,53	Lmax = = 3,201	Сумма		6,35	1,45	Lmax = = 3,187
				ИС=0,1					ИС=0,09
				ОС=0,17					ОС=0,16

Для понимания существа представленных в табл. 4.8 расчетных данных приведем систему последовательных вычислений по каждому из шести критериев.

Критерий 1. Объем валовой прибыли:

1. Вычисление оценки компонент собственного вектора по строкам:

; ; .

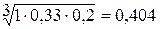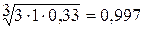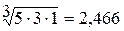2. Просуммируем оценки компонент собственного вектора:

0,404 + 0,997 + 2,466 = 3,867.

3. Определим оценки нормализованного вектора приоритетов по строкам:

0,404 : 3,867 = 0,104; 0,997 : 3,867 = 0,258.; 2,466 : 3,867 = 0,638.

4. Определим наибольшее собственное значение матрицы суждений (Lmax):

9 × 0,104 = 0,936; 4,33 × 0,258 = 1,117; 1,53 × 0,638 = 1,007.

Lmax = 0,936 + 1,117 + 1,007 = 3,061

5. Рассчитаем индекс согласованности (ИС): ИС = (3,031 - 3) : 2 = 0,03.

6. Рассчитаем отношение согласованности: ОС = 0,03 : 0,58 = 0,05.

Критерий 2. Объем выпуска (реализации) готовой продукции:

1. Вычисление оценки компонент собственного вектора по строкам:

; ; .

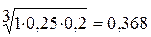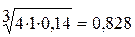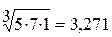2. Просуммируем оценки компонент собственного вектора:

0,368 + 0,824 + 3,271 = 4,463.

3. Определим оценки нормализованного вектора приоритетов по строкам:

0,368 : 4,463 = 0,082; 0,824 : 4,463 = 0,184; 3,271 : 4,463 = 0,733.

4. Определим наибольшее собственное значение матрицы суждений (Lmax):

10 × 0,082 = 0,82; 8,25 × 0,184 = 1,518; 1,34 × 0,733 = 0,982.

Lmax = 0,82 + 1,518 + 0,982 = 3,12.

5. Рассчитаем индекс согласованности (ИС):

ИС = (3,12 - 3) : 2 = 0,06.

6. Рассчитаем отношение согласованности (ОС): ОС = 0,06 : 0,58 = 0,103.

Критерий 3. Совокупная себестоимость, запланированной к выпуску продукции:

1. Вычисление оценки компонент собственного вектора по строкам:

; ;

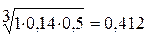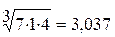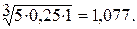
2. Просуммируем оценки компонент собственного вектора:

0,412 + 3,037 + 1,077 = 4,526.

3. Определим оценки нормализованного вектора приоритетов по строкам:

0.412 : 4,526 = 0,091; 3,037 : 4,526 = 0,671; 1,077 : 4,526 = 0,238.

4. Определим наибольшее собственное значение матрицы суждений (Lmax):

13 × 0,091 = 1,183; 1,39 × 0,671 = 0,933; 5,5 × 0,238 = 1,309.

Lmax= 1,183 + 0,933 + 1,309 = 4,526.

5. Рассчитаем индекс согласованности (ИС): ИС = (4,526 - 3) : 2 = 0,08.

6. Рассчитаем отношение согласованности (ОС): 0,08 : 0,58 = 0,14.

Критерий 4. Объем средств, связанных в запасах готовой продукции на складе:

1. Вычисление оценки компонент собственного вектора по строкам:

; ; .

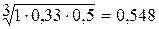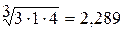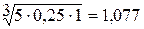2. Просуммируем оценки компонент собственного вектора:

0,548 + 2,289 + 1,077 = 3,914.

3. Определим оценки нормализованного вектора приоритетов по строкам:

0,548 : 3,914 = 0,14; 2,289 : 3,914 = 0,585; 1,077 : 3,914 = 0,275.

4. Определим наибольшее собственное значение матрицы суждений (Lmax):

9 × 0,14 = 1,26; 1,58 × 0,585 = 0,924; 5,5 × 0,275 = 1,513.

Lmax = 1,26 + 0,924 + 1,513 = 3,217.

5. Рассчитаем индекс согласованности (ИС): ИС = (3,217 - 3) : 2 = 0,11.

6. Рассчитаем отношение согласованности (ОС): ОС = 0,11: 0,58 = 0,19.

Критерий 5. Уровень использования производственной мощности предприятия:

1. Вычисление оценки компонент собственного вектора по строкам:

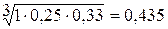
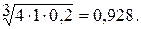
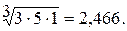
2. Просуммируем оценки компонент собственного вектора:

0,435 + 0,928 + 2,466 = 3,829.

3. Определим оценки нормализованного вектора приоритетов по строкам:

0,435 : 3,992 = 0,108; 0,843 : 3,992 = 0,211. 2,714 : 3,992 = 0,679.

4. Определим наибольшее собственное значение матрицы суждений (Lmax):

0,114 × 8 = 0,912; 6,25 × 0,242 = 1,513; 1,53 × 0,644 = 0,985.

Lmax= 0,912 + 1,513 + 0,985 = 3,201.

5. Рассчитаем индекс согласованности (ИС): ИС = (3,201 - 3) : 2 = 0,1.

6. Рассчитаем отношение согласованности (ОС): ОС = 0,1: 0,58 = 0,17.

Критерий 6. Доля осваиваемого целевого рынка:

1. Вычисление оценки компонент собственного вектора по строкам:

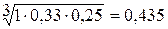
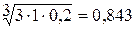
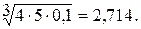
2. Просуммируем оценки компонент собственного вектора:

0,435 + 0,843 + 2,714= 3,992.

3. Определим оценки нормализованного вектора приоритетов по строкам:

0,435 : 3,992 = 0,108; 0,843 : 3,992 = 0,211; 2,714 : 3,992 = 0,679.

4. Определим наибольшее собственное значение матрицы суждений (Lmax):

8 × 0,108 = 0,864; 6,35 × 0,211 = 1,339; 1,45 × 0,679 = 0,984.

Lmax= 0,864 + 1,339 + 0,984 = 3,187.

5. Рассчитаем индекс согласованности (ИС): ИС = (3,187 - 3) : 2 = 0,09.

6. Рассчитаем отношение согласованности (ОС): ОС = 0,09 : 0,58 = 0,16.

Определяем численные значения глобальных приоритетов. Результаты расчетов приведем в табл. 4.9.

Таблица 4.9

Результаты расчетов глобальных приоритетов

Номер критерия	Глобальный приоритет
Численное значение вектора приоритета
0,309	0,242	0,177	0,0044	0,031	0,196
0,104	0,082	0,091	0,14	0,114	0,108	0,099 Альтернатива - А
0,258	0,184	0,671	0,585	0,242	0,211	0,319 Альтернатива - Б
0,637	0,733	0,238	0,275	0,644	0,679	0,554 Альтернатива-В

Числовые данные в табл. 4.9 получены следующим образом.

Глобальный приоритет по альтернативе А составит:

0,104× 0,309+0,082× 0,242+0,091× 0,177+0,14× 0,044+0,114× 0,031=

0,108× 0,196 = 0,099.

Глобальный приоритет по альтернативе Б составит:

0,258×0,309+0,184× 0,242+0,671× 0,177+0,585× 0,044+0,242× 0,031+0,211× 0,196 = 0,319.

Глобальный приоритет по альтернативе В составит:

0,637× 0,309+0,733× 0,242+0,238× 0,177+0,275× 0,0044+ 0,644× 0,031+

+0,679× 0,196 = 0,554.

Как следует из представленных в табл.4.9 расчетов, самым лучшим вариантом сформированной производственной программы предприятия является вариант В, так как у него оказался самый наивысший глобальный приоритет (0,544).

Основные преимущества МАИ заключаются в следующем:

1) он совмещает в себе достоинства аналитических и экспертных методов;

2) обеспечивает реализацию наиболее эффективного способа оценки количественно неизмеримых, но вместе с тем важных факторов для принятия обоснованных решений;

3) не предусматривает введения ограничения на транзитивность (метод работает с несогласованными суждениями и не требует, чтобы предпочтения потребителей или ЛПР соответствовали аксиомам полезности);

4) позволяет сводить исследования сложных проблем к достаточно простой процедуре проведения последовательно попарных сравнений;

5) не предполагает прямого определения коэффициентов важности (весомостей) по показателям, используемым для оценки качества решения задачи;

6) несложен в реализации, а также не требует больших финансовых и временных ресурсов на проведение необходимых расчетов;

7) позволяет решать задачи с практически неограниченным количеством критериев;

8) достаточно легко поддается программированию и реализации на ЭВМ.

Возможные и экономически целесообразные области использования МАИ весьма разнообразны. Он вполне применим, к примеру, для решения следующего комплекса задач, связанных с обоснованием выбора:

- наиболее эффективного источника финансирования бизнес-проекта;

- наиболее удачного с экономической точки зрения места строительства коммерческой фирмы;

- эффективного способа доставки груза до торговой точки;

- перспективных рынков сбыта готовой продукции;

- конкурентоспособного товара;

- наиболее эффективного варианта расходования средств на рекламу;

- предпочтительного варианта размещения свободных денежных средств предприятия в определенные виды ценных бумаг (формирование оптимального портфеля ценных бумаг);

- наиболее эффективной системы сбытовой сети товара;

- экономически целесообразного способа амортизации производственных фондов предприятия и др.

Таблица 4.3

Шкала относительной важности сравниваемых элементов

Интенсивность относительной важности	Определение	Объяснения
	Равная важность	Равный вклад двух видов деятельности в цель
	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одному виду деятельности над другим
	Существенное или сильное превосходство	Опыт и суждения дают сильное превосходство, что оно становится практически значительным
	Очень сильное превосходство	Очевидность одного вида деятельности над другим подтверждается наиболее сильно
2, 4, 6, 8,7	Промежуточные решения между двумя суждениями	Применяются в компромиссном случае
Обратные величины приведенных выше чисел	Если при сравнении одного вида деятельности с другим получено одно из вышеуказанных чисел (например, 3), то при сравнении второго вида деятельности с первым получим обратную величину (т.е. 1/3)	-