Решение задачи с применением табличного процессора EXCEL. Программирование арифметического цикла
Программирование арифметического цикла
Постановка задачи
Разработать алгоритм и составить программу табулирования (вычисления таблицы значений) функции для произвольного диапазона изменения независимого параметра или аргумента. Выполнить расчет для заданных значений исходных данных.
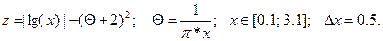 |
Анализ задачи
Задача заключается в многократном вычислении значений промежуточной функции Q и итоговой функции z при изменении аргумента х от начального значения хН=0,1 до конечного значения хК=3,1 с шагом Dх=0,5. Исходных данных для расчета достаточно.
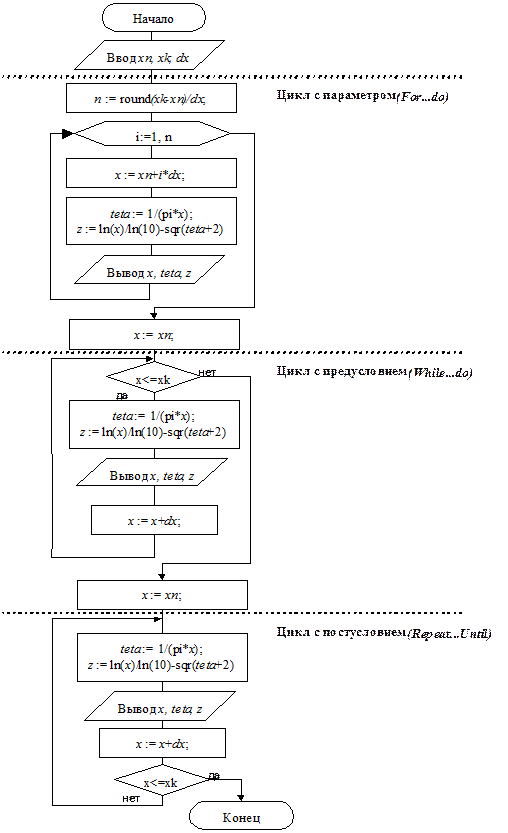
Задачу будем решать, последовательно применяя различные типы циклов: цикл с параметром (For¼do), цикл с предусловием (While¼do) и цикл с постусловием (Repeat¼Until).
Таблица переменных
| Смысл переменных | Обозначение переменных | Тип переменной | |
| в задаче | в алгоритме | ||
| Исходные данные: начальное значение аргумента конечное значение аргумента шаг изменения аргумента | хН хК Dх | xn xk dx | Вещественный |
| Промежуточные данные: результат промежуточной функции текущее значение аргумента число шагов (для цикла For¼do) параметр цикла For¼do | Q х – – | Teta х n i | Вещественный Вещественный Целочисленный Целочисленный |
| Результаты: Значение итоговой функции | z | Z | Вещественный |
Блок-схема алгоритма
 |
Интерфейс программы
Ввод исходных данных запланируем в форме диалога: значения xn, xk и dx будем вводить с клавиатуры при появлении соответствующего запроса на экране монитора после запуска программы.
Предусмотрим вывод очередного значения аргумента х и значений функций Teta и Z на экран монитора в виде таблицы.
Текст программы на языке Паскаль
Program Lab2;
var xn, xk, dx, x, teta, z: real;
i, n: integer;
BEGIN
write('Vvedite xn, xk, dx => ');
readln(xn, xk, dx);
writeln;
writeln('REZULTAT:');
writeln('1. For...Do (s parametrom)');
n:=trunc((xk-xn)/dx)+1;
for i:=0 to n-1 do
begin
x:=xn+i*dx;
teta:=1/(pi*x);
z:=abs(ln(x)/ln(10))-sqr(teta+2);
writeln('X= ', x:4:2, ' Teta= ', teta:6:3, ' Z= ', z:6:3);
end;
writeln;
writeln('2. While...Do (s predusloviem)');
x:=xn;
While x<=xk do
begin
teta:=1/(pi*x);
z:=abs(ln(x)/ln(10))-sqr(teta+2);
writeln('X= ', x:4:2, ' Teta= ', teta:6:3, ' Z= ', z:6:3);
x:=x+dx;
end;
writeln;
writeln('3. Repeat...Until (s postusloviem)');
x:=xn;
repeat
teta:=1/(pi*x);
z:=abs(ln(x)/ln(10))-sqr(teta+2);
writeln('X= ', x:4:2, ' Teta= ', teta:6:3, ' Z= ', z:6:3);
x:=x+dx;
until x>=xk;
END.
Результаты расчета
Для контрольного расчета выберем значение аргумента х, лежащее внутри заданного диапазона изменения аргумента.
Для Х=1.1 получаем Teta=0.286, Z=–5.202. Для проверки правильности работы запустим программу при заданных значениях исходных данных.
Результаты расчета для заданных значений исходных данных:
Vvedite xn, xk, dx => 0.1 3.1 0.5
REZULTAT
1. For...Do (s parametrom)
X= 0.10 Teta= 3.183 Z= -25.865
X= 0.60 Teta= 0.531 Z= -6.182
X= 1.10 Teta= 0.289 Z= -5.200
X= 1.60 Teta= 0.199 Z= -4.631
X= 2.10 Teta= 0.152 Z= -4.307
X= 2.60 Teta= 0.122 Z= -4.090
X= 3.10 Teta= 0.103 Z= -3.930
2. While¼Do (s predusloviem)
X= 0.10 Teta= 3.183 Z= -25.865
X= 0.60 Teta= 0.531 Z= -6.182
X= 1.10 Teta= 0.289 Z= -5.200
X= 1.60 Teta= 0.199 Z= -4.631
X= 2.10 Teta= 0.152 Z= -4.307
X= 2.60 Teta= 0.122 Z= -4.090
X= 3.10 Teta= 0.103 Z= -3.930
3. Repeat¼Until (s postusloviem)
X= 0.10 Teta= 3.183 Z= -25.865
X= 0.60 Teta= 0.531 Z= -6.182
X= 1.10 Teta= 0.289 Z= -5.200
X= 1.60 Teta= 0.199 Z= -4.631
X= 2.10 Teta= 0.152 Z= -4.307
X= 2.60 Teta= 0.122 Z= -4.090
X= 3.10 Teta= 0.103 Z= -3.930
Результаты контрольного расчета и результаты работы программы при Х=1.1 совпадают. Результаты расчетов, выполненных для трех типов циклов, также полностью совпадают. Поэтому можно сделать вывод, что алгоритм и программа были составлены верно.
Решение задачи с применением табличного процессора EXCEL
Для решения задачи предусмотрим возможность ввода произвольных исходных данных в отдельные ячейки таблицы. Текущие значения аргумента Х будем вычислять, жестко привязываясь к ячейкам, содержащим начальное значение аргумента ХНАЧ и значение шага изменения аргумента dX. Для этого, при ссылках на них будем применять абсолютную адресацию этих ячеек.
В результате, таблица будет выглядеть следующим образом.
| A | B | C | |
| ИСХОДНЫЕ ДАННЫЕ | |||
| Ввод Хнач | Ввод Хкон | Ввод dX | |
| 0,1 | 3,1 | 0,5 | |
| РЕЗУЛЬТАТЫ РАСЧЕТА | |||
| X | Teta | Z | |
| 0,10 | 3,183 | – 25,865 | |
| 0,60 | 0,531 | – 6,183 | |
| 1,10 | 0,290 | – 5,201 | |
| 1,60 | 0,199 | – 4,632 | |
| 2,10 | 0,152 | – 4,307 | |
| 2,60 | 0,122 | – 4,090 | |
| 3,10 | 0,103 | – 3,930 |
В ячейки А3, В3 и С3 вводятся соответственно значения Хнач, Хкон и dX.
В ячейку А7 вводится абсолютная ссылка на ячейку А3, содержащую начальное значение аргумента Хнач: =$A$3.
В ячейку А8 вводится формула для вычисления очередного значения Х – к предыдущему значению Х прибавляется шаг dX: =A7+$C$3.
Ячейки А9и ниже заполняем протаскиванием ячейки А8 до тех пор, пока не получим конечное значение, равное Хкон.
В ячейку В7 вводим формулу для вычисления значения промежуточной функции Teta: =1/(ПИ*А7). Ячейки В8–В13 заполняем протаскиванием ячейки В7.
В ячейку С7 вводится формула для вычисления итоговой функции Z.
=ABS(LOG10(A7))-(B7+2)^2
Ячейки С8–С13 заполняются протаскиванием ячейки С7.
Результаты расчета с применением составленной программы и с помощью табличного процессора EXCEL совпадают.
