Гнвеп лтоаа дрнев теьио рпотм бчмор соыьи.
Жіберілетін хабарламаны бұдан да толығырақ жасауы қажет болса, бір рет шифрлағаннан кейін, тағы да қайта шифрлауға болады. Мұндай шифрлау екілік орын алмастыру деп аталады. Бұл жағдайда орын алмастырулар бағандар және жолдар үшін жеке-жеке анықталады. Алдымен, кестеге хабарлама мәтіні жазылады, содан соң бағандар, кейін жолдар орын ауыстырылады. Мысалы: «ПРИЛЕТАЮ ВОСЬМОГО» сөзін шифрлау қажет. Ескілік орын алмастыруларда кілт ретінде берілген кестенің бағандар номерлері және жолдар номерлері тізбегі қолданылады.
| а) | б) | в) | ||||||||||||||
| П | Р | И | Л | Р | Л | И | П | Т | Ю | А | Е | |||||
| Е | Т | А | Ю | Т | Ю | А | Е | О | О | Г | М | |||||
| В | О | С | Ь | О | Ь | С | В | Р | Л | И | П | |||||
| М | О | Г | О | О | О | Г | М | О | Ь | С | В |
а) берілген кесте; б) бағандардың орын алмасуы; в) жолдардың орын алмасуы.
Егерде алынған мәтінді 4 әріптен топтайтын болсақ,
«ТЮАЕ ООГМ РЛИП ОЬСВ» хабарламасы шығады.
Кәдімгі алгебрадан басқа арнайы алгебра бар. Оның негізін ХІХ ғ. математигі Дж. Буль салған. Бұл алгебра пікірлерді есептеумен айналысады.
Оның ерекшелігі дискреттік құрылғылардың жұмысын сипаттауға қолдану болып келеді. Ондай құрылғылар қатарына есептеу техникасы және автоматика құрылғыларының бір классы жатады.
Мұнда алгебраның өзі құрылғының үлгісі рөлін атқарады. Ол көрсетілген типтегі еркін құрылғының жұмысы осы алгебраның көмегімен қандай да бір жағынан тек қана сипатталуы мүмкін дегенді білдіреді. Шындығында нақты құрылғы физикалық логика алгебрасында сипатталғанна бөлек жұмыс істейді.
Логика алгебрасының функцияларына қатысты бірнеше синонимдер бар:
1. логика алгебрасының функциялары;
2. ауыстырып қосқыш функциялары;
3. бульдік функциялар;
4. екілік функциялар.
Қажеттілігінше бұл синонимдердің барлығын пайдаланамыз.
Аргументтердің қандай да бір жиынын қарастырайық:
<X1,X2,X3,...Хi,...Xn>және де аргументтердің әрқайсысы басқаларынан тәуелсіз екі мүмкін мәннің біреуін қабылдайды деп келісеміз.
Бір және екі айнымалыға тәуелді бірнеше бульдік функцияларды қарастырайық.
Ол үшін аргументтердің барлық терімдеріне оның мәндерін беру керек.
| Х аргументі | Мәндер | Функцияның аты | |
| F0(x) | '0' тұрақтысы | ||
| F2(x) | 'х' айнымалысы | ||
| F3(x) | 'х' (х–ті теріске шығару) инверсиясы | ||
| F4(x) | '1' тұрақтысы |
Екі аргументке тәуелді барлық ЛАФ–ын қарастырайық та оларды бір кестеге жазайық:
| Функция № | Логикалық айнымалы теріміндегі функция мәні | Функция аты | Функцияның белгіленуі | |||
| X1 | ||||||
| X2 | ||||||
| f0(X1,X2) | "нөл" тұрақтысы | f(X1,X2)=0 | ||||
| f1(X1,X2) | Конъюнкция, көбейтінді. | f(X1,X2)= X1& X2f(X1,X2)= X1 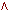 X2f(X1,X2)= X1 · X2f(X1,X2)= X1 X2 X2f(X1,X2)= X1 · X2f(X1,X2)= X1 X2 | ||||
| f2(X1,X2) | X2 бойынша тйым салу | X1 Δ X2 | ||||
| f3(X1,X2) | X1 айнымалысы | f(X1,X2)= X1 | ||||
| f4(X1,X2) | X1 бойынша тйым салу | X2 Δ X1 | ||||
| f5(X1,X2) | X2 айнымалысы | f(X1,X2)= X2 | ||||
| f6(X1,X2) | mod2 бойынша қосу (бірмәнділік емес) | f(X1,X2)= X1  X2 X2 | ||||
| f7(X1,X2) | Дизъюнкция | f(X1,X2)= X1 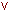 X2f(X1, X2)= X1+ X2 X2f(X1, X2)= X1+ X2 | ||||
| f8(X1,X2) | Пирса тілсызығы | f(X1, X2)= X1  X2 X2 | ||||
| f9(X1,X2) | Бірмәнділік | f(X1, X2)= X1  X2f(X1, X2)= X1~X2 X2f(X1, X2)= X1~X2 | ||||
| f10(X1,X2) | X2 инверсиясы | f(X1, X2)=^X2f(X1, X2)=X2 | ||||
| f11(X1,X2) | X2-ден X1-ге импликация | f(X1, X2)= X2  X1 X1 | ||||
| f12(X1,X2) | X1 инверсиясы | f(X1, X2)=^X1f(X1, X2) = X1 | ||||
| f13(X1,X2) | X1-ден X2-ге импликация | f(X1, X2)= X1  X2 X2 | ||||
| f14(X1,X2) | Шеффер штрихы | f(X1, X2)= X1|X2 | ||||
| f15(X1,X2) | Тұрақты "бірлік" | f(X1, X2)=1 |
Лекция
